Journal of the Pancreas Open Access

Keywords

Alkaline Phosphatase; Bilirubin

Abbreviations

ALP alkaline phosphatase; TB total bilirubin

INTRODUCTION

A vital organ of human being is liver which has various important functions such as protein synthesis, decomposition of red blood cells, detoxification, glycogen storage, and production of biochemical and hormone. The liver has multidimensional functions, and it is also prone to many diseases. Note that there are more than 100 different forms of known liver disease caused by many risk factors [1, 2, 3]. The most common disease throughout the world is the liver disease which is caused by damaged or inflammation hepatocyte in liver [4, 5, 6, 7]. In every year, throughout the world, more than one million of new liver cancer patients are diagnosed [8]. Even more dreadful is the real situation that liver cancer is not easily identified, as the liver is able to maintain regular activity even if there are some partially damaged. The imaging diagnosis of early stage hepatic cirrhosis, hepatitis, and hepatic fibrosis is still very complicated as they lack morphological changes. However, a few hemodynamic changes of the liver diseases are generally observed [8, 9]. The most important steps in liver cancer treatment is the early diagnosis of the disease.

Many research articles have pointed that dietary factors have great effects on liver biochemical markers [8, 10, 11]. In animals or healthy humans, fat ingestion has been identified to elevate serum ALP levels. It is happened either if a high-fat diet is absorbed or if fat is included in a test meal [12, 13, 14]. Intravenous infusion of glucose in rabbits develops an increase in the hepatic excretion of conjugated bilirubin [15]. A few medium-chain fatty acids decrease in binding of bilirubin to albumin in vitro [16]. In practice, excess alcohol consumed (>80 g/day for more than 5 years) (excluding other causes of cirrhosis) may produce alcoholic cirrhosis [12, 17].

There is a little study on the explanatory factors of serum alkaline phosphatase (ALP), considering the real fact that it is non-normal, heteroscedastic and positive. It is identified that the response ALP is heterogeneous, and non-normally distributed. Therefore, ALP should be analyzed by joint generalized linear models (JGLMs) namely, gamma or Log-normal [18, 19, 20, 21]. In order to confirm the analysis, the present considered data set has been analyzed using both the gamma and Log-normal joint generalized linear models. It is found that joint Log-normal models give better results. Both the analysis results are given in the article.

The article attempts to know the answer of the following quarries or hypotheses. What are the explanatory factors or determinants of the serum alkaline phosphatase (ALP)? How are the explanatory factors correlated with the ALP? What are the functional activities of the explanatory factors on ALP? These quarries or hypotheses are evaluated in the article, using a real data set of 583 subjects with 9 continuous variables and 2 attribute characters.

MATERIALS AND STATISTICAL METHODOLOGY

Materials

The current report considers a real data set of 583 subjects with 9 continuous variables and 2 attribute characters. The data set was collected from the North-East of Andhra Pradesh, India. The data set can be obtained from https://archive.ics.uci.edu/ml/machine-learningdatabases/ 00225/. The statement of the explanatory variables, and levels of the attribute characters are given in Table 1. The descriptive statistics such as the proportion, mean, normal range of the biochemical parameters, and standard deviation are displayed in Table 1. There are 75.82% male patients, and 24.18% female patients. Liver patients (71.5%) are more than the non-liver patients (28.5%) in the given data set. The statement of the subject population and the information collection method are displayed in [22, 23]. This is not described again in the report.

Statistical Methods

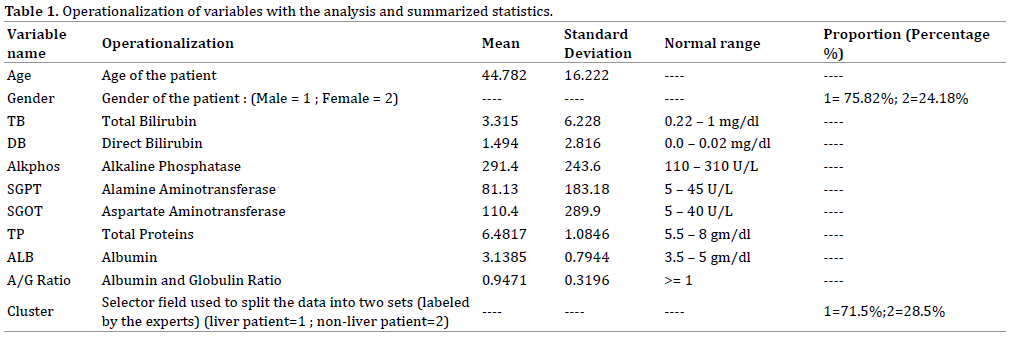
The usual regression models consider that the variance of the response (Y) is constant within the whole range of the variable. However, this assumption is not true always [24]. Generally, biochemical data are heterogeneous. For example, the ALP values for the liver disease patients are heterogeneous. In order to remove the non-constant variance of a data set, the log-transformation is generally used, but practically, the heteroscadasticity of the data set may not always be removed [24, Table 2].

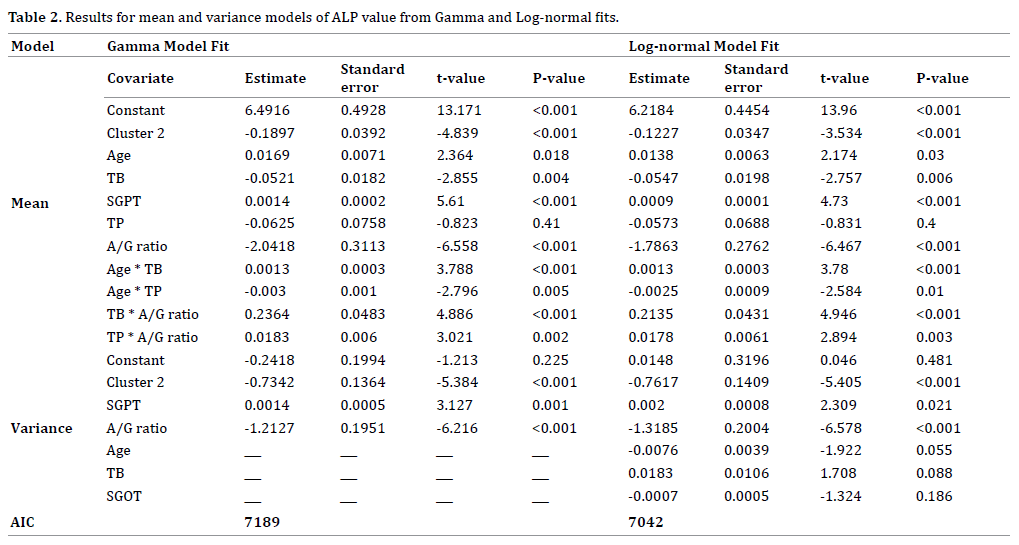
Positive data from the continuous variables with constant variance or constant coefficient of variation may be analyzed either by the Log-normal or the gamma models [21]. Generally, physiological data are heterogeneous, so these two models may not give similar results [19, 20, 25, 26, 28]. In practice, generalized linear models class is used to analyze non-normal, heteroscedastic and positive data set. Generally, the mean and variance of the response variable may be related in the generalized linear models, as a result the variance of the response may be non-constant. For the analysis of non-constant variance positive data y_i ’s, Nelder and Lee [28] have suggested to use the joint generalized linear models (JGLMs). A detailed discussion of JGLMs is given in [18, 19, 27, 28]. For ready reference, a short description of the JGLMs is reproduced herein.

For the positive data Y_i ’s, when

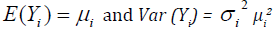
The log transformation Z_i = log (Y_i) is used to stabilize the variance Var 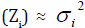. If one needs better models, an improved statistical tool is used. Generally, the variance may not be stabilized always by a simple transformation [24]. Then Nelder and Lee [28] have suggested to use JGLMs.

For the positive dependent variable Y_i, the log transformation Z_i = logY_i is applied. The joint modeling for the mean and variance under Log-normal distribution is given by

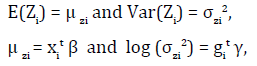
where xit and git denote respectively, the row vectors for the regression coefficients β (mean model) and γ (variance model).

For the positive dependent variable y_i ’s, if

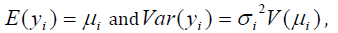
where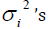 are the dispersion parameters and 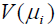is the variance function. In generalized linear models, the variance has two portions. One portion is 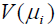that depends on the mean values. The other portion is σ_i² that is free of mean values. The variance function identifies the distribution family in GLMs. For example, the distribution is gamma if 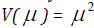, Poisson if 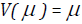, and Normal if 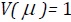, etc.

The mean and variance models of JGLMs are

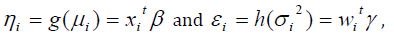
where g(⋅) and h(⋅) are respectively the GLM link functions for mean and variance, and 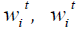denote respectively, the row vectors for the regression coefficients β (mean model) and γ (variance model). Maximum likelihood (ML) method is used to estimate β (mean model), and restricted ML (REML) method is used to estimate γ (variance model) [18, 19].

It is well-known that the serum alkaline phosphatase (ALP) is a liver biomarker. Higher than normal levels of ALP (Table 1) in blood may indicate a problem with liver or gall bladder. This could include hepatitis (infection), cirrhosis (scarring), liver cancer, gallstones, or a blockage in our bile ducts. The article considers ALP as the dependent variable to examine the hypotheses as stated in Introduction. The response serum alkaline phosphatase is positive with non-constant variance, and it belongs to exponential family distribution. Therefore, such data are generally, analyzed by the Log-normal or gamma models as stated above. In order to confirm the derived results, both the above models are used to perform the analysis. Now we are interested to investigate the following using both the models. What are the approximate true models of ALP for the liver disease patients? What are the explanatory factors (or determinants) of ALP? What are the effects of the explanatory factors on the ALP? These quarries are addressed in the next sections.

Alkaline Phosphate (ALP) Value Analysis, Results and Interpretations

Analysis: Alkaline phosphate (ALP) value is the continuous positive response random variable of interest in the article. There are remaining 8 continuous, and 2 attribute explanatory variables. In case of attribute factors, we have considered the constraint that the effects of the first levels are zero. Hence, for each attribute factor, the first level is considered as the reference level by estimating it as zero. The main effect of A is denoted by a_i for i = 1, 2, 3. We have considered 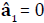, so that 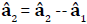. Therefore, the estimate of the effect A2 is the difference between the second and the first levels in the main effect A.

Alkaline phosphate vale is considered as the response variable in the current analysis and the rest other variables or factors are considered as the explanatory variables. We have modeled the response ALP using both the Log-normal and gamma models [18, 19]. The final fitted models have been selected on the basis of smallest Akaike information criterion (AIC) value in each class. It is known that the AIC selects a model which minimizes the predicted additive errors and squared error loss [28]. The Log-normal and the gamma fitted models results of ALP are given in Table 2. Table 2 shows that the Log-normal fitted models (AIC= 7042) give better results than the gamma fitted models (AIC=7189). It is not always necessary that all the selected effects are significant [29]. Some insignificant effects are retained in the model in order to respect the marginality rule, namely that when an interaction term is significant all related lower-order interactions and main effects should be included in the model [30]. In epidemiology, statistical insignificant included factors or variables in the fitted models are known as confounder. For model checking diagnosis plots, we have plotted the absolute residuals and normal probability plots for the fitted joint Log-normal models (Table 2) as they are better fitted models.

Figure 1(a) presents the absolute residuals plot of the fitted Log-normal models (Table 2) with respect to fitted values. It is a straight flat diagram, implying that the variance is constant with the running means. The normal probability plot for the fitted mean model of Log-normal fit (Table 2) is given in Figure 1(b). There is no lack of fit, or systematic departure in the Figure 1(b). Therefore, the fitted Log-normal models (Table 2) are approximate true models of ALP.

RESULTS

The mean serum alkaline phosphatase (ALP) is negatively associated with the types of liver patients (P<0.001), or total bilirubin (TB) (P=0.006), or albumin to globulin ratio (A/G) (P<0.001), or interaction effects of albumin to globulin ratio (A/G) with total proteins (TP) (A/G*TP) (P=0.003). The mean ALP is positively associated with the age (P= 0.030), or SGPT (P<0.001), or interaction effect of age with total bilirubin (TB) (Age*TB) (P<0.001), or interaction effect of albumin to globulin ratio (A/G) with the total bilirubin (TB) (A/G*TB) (P<0.001), or interaction effect of albumin to globulin ratio (A/G) with total proteins (TP) (A/G*TP) (P=0.003).

The variance of serum alkaline phosphatase is negatively associated with the types of liver patients (P<0.001), or albumin to globulin ratio (A/G) (P<0.001), or age (P=0.055), or SGOT (P=0.186). The ALP variance is positively associated with the SGPT (P<0.001), or total bilirubin (TB) (P=0.088).

Interpretations of Liver Disease Data Analysis

Summarized results of the serum alkaline phosphatase value analysis are given in Table 2. Table 2 presents results of joint gamma and Log-normal models. Note that joint Log-normal models give better results. Therefore, the following interpretations are drawn based on Log-normal models (Table 2).

*The mean alkaline phosphates (ALP) is negatively significantly correlated with the patient types (liver patient=1, non-liver patient=2) (P<0.001). This indicates that ALP value is higher for liver disease patients than nonliver patients.

*The mean ALP is positively correlated with the subjects age (P=0.030), implying that the mean ALP value increases at senior ages.

*The mean ALP is negatively significantly correlated with the total bilirubin (TB) (P=0.006), indicating that the total bilirubin increases as the ALP value decreases.

*The mean ALP is positively significantly correlated with Alamine Aminotransferase (SGPT) (P<0.001), indicating that the mean ALP increases as the SGPT increases.

*The mean ALP is negatively significantly correlated with the Albumin to globulin ratio (A/G) (P<0.001), indicating that the mean ALP increases as the A/G ratio decreases.

*The mean ALP is positively significant associated with the interaction effect of age and the total bilirubin (TB) (Age*TB) (P<0.001), indicating that the ALP increases as the interaction effect (Age*TB) increases.

*The mean ALP is negatively significant associated with the interaction effect of age and the total protein (TP) (Age*TP) (P=0.010), indicating that the ALP increases as the interaction effect (Age*TP) decreases.

*The mean ALP is positively significant associated with the interaction effect of total bilirubin (TB) and the Albumin to globulin ratio (A/G) (TB*A/G) (P<0.001), implying that the ALP increases as the interaction effect (TB*A/G) increases.

*The mean ALP is directly significantly correlated with the interaction effect of total protein (TP) and the Albumin to globulin ratio (A/G) (TP*A/G) (P=0.003), indicating that the ALP increases as the interaction effect (TP*A/G) increases.

*The variance of Alkaline Phosphates (ALP) is inversely significantly correlated with the patient’s type (liver patient=1, non-liver patient=2) (P<0.001), implying that the ALP variance is higher for liver patients than the nonliver patients.

*The ALP variance is directly significantly correlated with Alamine Aminotransferase (SGPT) (P=0.021), implying that the ALP variance increases as the SGPT increases.

*The ALP variance is reciprocally significantly correlated with the Albumin to globulin ratio (A/G) (P<0.001), indicating that the ALP variance decreses as the A/G ratio increases.

*The ALP variance is reciprocally significantly correlated with the age (P=0.055), implying that the ALP variance is higher at junior ages.

*The ALP variance is directly significantly correlated with the total bilurubin (TB) (P= 0.088), indicating that the ALP variance increases as TB increases.

The final fitted Log-normal mean and variance models (Table 2) of ALP value of the liver patients, respectively, are

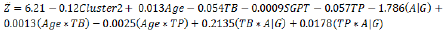
and

DISCUSSION

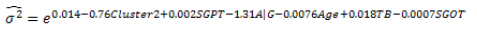
The article has considered Alkaline Phosphates (ALP) as the dependent variable. The estimated ALP values can be derived from the fitted Log-normal models. Fitted results for the two models are given in Table 2. These two fitted models show very close results, except a few additional covariates included in the fitted Log-normal variance model. The explanatory factors of the ALP values have been derived in the article using the fitted Log-normal models (Table 2).

It has been identified in the article that the mean alkaline phosphatase (ALP) value is higher for the liver patients than non-liver patients. It is higher at senior ages of the liver patients than the junior ages. It decreases as the total bilirubin increases, while it increases as the SGPT increases. The mean ALP decreases as the albumin to globulin ratio increases. Interaction effect such as age with total bilirubin (TB) (Age*TB), age with total proteins (TP) (Age*TP), albumin to globulin ratio (A/G) with the total bilirubin (TB) (A/G*TB), total proteins (TP) with albumin to globulin ratio (A/G) (A/G*TP) are significant effects on the mean ALP.

The article has considered 583 patients with all nonmissing information. The current results are not similar to earlier results. For example, SGOT is not a significant determinant of the ALP (Table 2) in the present report, but it is significant in some other articles [31, 32]. Similarly, age, total bilirubin (TB), albumin to globulin ratio (A/G ratio) are significant factors for ALP in the present article, but these factors are not significant in the previous articles [17]. In the present report, many interaction effects such as Age*TB, Age*TP, TB*A/G, TP*A/G are significant on the mean ALP (Table 2), which are not reported in the earlier reports. Many ALP variance determinants such as patient’s type, SGPT, age, albumin to globulin ratio, total bilirubin, SGOT are significant in the present reports which are not reported in the previous articles [31, 32].

CONCLUSION

The current models may provide many determinants of Alkaline Phosphates. Based on the present results, it may be possible to take the necessary action to control the Alkaline Phosphates value. Medical practitioners, researchers and the liver patients may be benefited from the current report. Every individual should care on Alkaline Phosphates values at older ages. Note that at older ages with higher values of total bilirubin, and total protein increase the Alkaline Phosphates values.

Conflict of Interest

The authors confirm that this article content has no conflict of interest.

References

1. Rang HP, Dale MM, Ritter JM, Moore PK. Pharmacology. 5th ed. Bath: Churchill Livingstone; 2003.
2. Robbins SL, Kumar V, Cotran RS. Robbins and Cotran Pathologic Basis of Disease. Philadelphia, PA: Saunders/Elsevier; 2010.
3. El-serag HB, Mason AC. Rising incidence of hepatocellular carcinoma in the United States. N Engl J Med 1999; 340:745-50. [PMID: 10072408]
4. Deuffic S, Poynard T, Buffat L, Valleron AJ. Trends in primary liver cancer. Lancet 1998; 351:214–215. [PMID: 9449893]
5. Godley PA, Sandler RS. Liver cancer, in: Digestive Diseases in the United States: Epidemiology and Impact, J.E. Everhart, ed., Washington, D.C., Government Printing Office, 1994; 227–241, (NIH publication no. 94–1447).
6. Kew MC. Hepatic tumors and cysts, in: Sleisenger & Fordtran’s Gastrointestinal and Liver Disease: Pathology/diagnosis/management, 6th ed, vol. 1, M. Feldman, M.H. Sleisenger and B.F. Scharschmidt, eds, Philadelphia: W.B., Saunders, 1998; 1363–1387.
7. Okuda K, Fujimoto I, Hanai A, Urano Y. Changing incidence of hepatocellular carcinoma in Japan. Cancer Res 1987; 47:4967–4972. [PMID: 3040235]
8. Deems RO, Friedman LS, Friedman MI, Munoz SJ, Deems DA, Maddrey WC. Relationship between liver biochemical tests and dietary intake in patients with liver disease. J Clin Gastroententerol 1994; 18: 304–308. [PMID: 8071515]
9. Lin RH. An intelligent model for liver disease diagnosis. Artif Intell Med 2009; 47:53–62.
10. Orrego H, Blendis LM, Crossley IR, Medline A, Macdonald A, Ritchie S, Israel Y, Correlation of intrahepatic pressure with collagen in the Dissespace and hepatomegaly in humans and in the rat. Gastroenterology 1981; 80:546–556. [PMID: 19540738]
11. Larkin FA, Metzner HL, Thompson FE, Flegal KM, Guire KE. Comparison of estimated nutrient intakes by food frequency and dietary records in adults. J Am Diet Assoc 1989; 89:215–223. [PMID: 2915094]
12. McDowell CM, Ross MH. Dietary fat, age and hepatic alkaline phosphatase activity in the rat. Growth 1966; 30:177–185. [PMID: 5963696]
13. Malagelada JR, Stolbach LL, Linscheer WG. Influence of carbon chain length of dietary fat on intestinal alkaline phosphatase in chylous ascites. Dig Dis 1977; 22:629–632. [PMID: 879129]
14. Young GP, Friedman S, Yedlin ST, Alpers DH. Effect of fat feeding on intestinal alkaline phosphatase activity in tissue and serum. Am J Physiol 1981; 241:461–468. [PMID: 7325238]
15. Munoz ME, Gonzalez J, Esteller A. Effects of glucose administration on bilirubin excretion in the rabbit. Experientia 1987; 43:166–168. [PMID: 2949996]
16. Brodersen R. Free bilirubin in blood plasma of the newborn: Effects of albumin, fatty acids, pH, displacing drugs, and phototherapy, in: Intensive Care in the Newborn, L. Stern, W. Oh and B. Friis-Hansen, eds, New York: Masson Publishing, 1978; 331–345.
17. Das RN. Relationships of liver biochemical parameters and effects of wine drinking. Model Assist Stat Appl 2013; 8:163–175.
18. Lee Y, Nelder JA, Pawitan Y. Generalized Linear Models with Random Effects (Unified Analysis via H-likelihood), Chapman & Hall, London, 2006.
19. Das RN, Lee Y. Log normal versus gamma models for analyzing data from quality-improvement experiments. Qual Eng 2009; 21:79-87.
20. Das RN, Park JS. Discrepancy in regression estimates between lognormal and gamma: Some case studies. J Applied Statistics 2012; 39:97-111.
21. Firth D. Multiplicative errors: log-normal or gamma? J R Stat Soc Series B Stat Methodol 1988; 50:266-268.
22. Ramana BV, Babu MSP, Venkateswarlu NB. A Critical Study of Selected Classification Algorithms for Liver Disease Diagnosis. Int J Database Manag Sys 2011; 3:101-14.
23. Ramana BV, Babu MSP. Liver Classification Using Modified Rotation Forest. Int J Eng Res Dev 2012; 1:17-24.
24. Myers RH, Montgomery DC, Vining GG. Generalized linear models with applications in engineering and the sciences. New York: John Wiley and Sons 2002.
25. Das RN, Mukherjee S, Panda RN. Association between Body Mass Index and Cardiac Parameters of Worcester Heart Attack Study. BAOJ Cell Mol Cardio 2016; 2:1-6.
26. Das RN, Mukherjee S. Joint Mean-Variance Overall Survival Time Fitted Models from Stage III Non-Small Cell Lung Cancer. Epidemiology (Sunnyvale) 2017; 7:296.
27. Das RN. Robust Response Surfaces, Regression, and Positive Data Analyses. Chapman & Hall, London, 2014.
28. Nelder JA, Lee Y. Generalized linear models for the analysis of Taguchi-type experiments. Appl Stoch Models Bus Ind 1991; 7:107-120.
29. Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning, Springer-Verlag, 2001.
30. Nelder JA. The statistics of linear models: back to basics. Statistics and Computing 1994; 4:221–234.
31. Babu MSP, Swapna K, Balakrishna T, Venkateswarlu NB. An Implementation of Hierarchical Clustering on Indian Liver Patient Dataset. Int J Emerg Technol Comput Appl Sci 2014; 8:543-547.
32. Ramana BV, Babu MSP, Venkateswarlu NB. A Critical Comparative Study of Liver Patients from USA and INDIA: An Exploratory Analysis. Int J Comput Sci 2012; 9:506-516.