Research Article - (2017) Volume 3, Issue 1
Ridha MS*
Structural Engineering, University of Technology, Iraq
*Corresponding Author:
Maha MS Ridha
Associate Professor
Structural Engineering
University of Technology, Iraq
Tel: (964) 79 01592170
E-mail: Dr.mahams@yahoo.com
Received Date: May 03, 2017; Accepted Date: May 17, 2017; Published Date: May 27, 2017
Citation: Ridha MS. Axial-Flexural Interaction of Square FRP Tube Columns In-filled with Ultra-High Performance Concrete. Polym Sci. 2017, 3:1.
More than a decade of studies have shown the benefits of ultra-high performance concrete (UHPC) on a ductility, energy absorption, crack distribution, damage tolerance, and deformation capacity. Nevertheless, little information is available on the behavior of UHPC columns especially when confined with fiber-reinforced polymers (FRP). This paper presents the results of experimental program and analytical modelling for performance evaluation of square FRP tubular columns in filled with UHPC under axial-flexural (P-M) loading. Eight steel–reinforced UHPC specimens were tested. Four had FRP tubes and subjected to initial load eccentricity 0, 10, 85 and 95 mm. Three reference columns without FRP tube and subjected to initial load eccentricities 0, 10, 85 mm. The last one had FRP tube and subjected to pure bending. P-M interaction diagram of FRP tubular columns in filled with UHPC were drawn using the obtained experimental results and compared against theoretical P-M interaction diagram that based on the principles of ACI building code. Good agreement between experimental and theoretical results was observed with COV 5.9%.
Keywords
Columns; Fiber-reinforced polymer; Ultra-high performance concrete
Introduction
In recent years, concrete-filled fiber-reinforced polymer (FRP) tubes have provided an attractive use of hybrid materials in several structural applications such as piles, columns, and bridge piers where the FRP tubes provided a permanent, noncorrosive, lightweight formwork for concrete and reinforcement element at the same time. Several researcher have studied the structural behaviour of conventional concrete-filled FRP tubes under concentric axial loads [1,2], flexural loading [3,4] and combined P-M loading [5,6]. Ultra-high performance concrete is a new construction material with exceptional properties such as higher strength, deformation capacity and toughness than conventional concrete. These superior materials properties are achieved due to low-water-cement ratio and presence of steel fibers which results to higher compressive strength (e.g. up to five times that of conventional concrete), higher tensile strength (e.g. up to ten times that of conventional concrete), and much greater ductility than conventional concrete [7].
Considering the excellent material properties of UHPC and FRP, Zoherevand and Mirmiran [8] developed a hybrid column made of a FRP tube filled with UHPC within the plastic hinge length and conventional concrete for the residuum of the length of column. The column was without steel reinforcement and tested under reverse cyclic lateral loading. The results showed significantly higher flexural strength, lower residual drift, and similar energy dissipation, as compared to conventional concrete column with steel reinforcement. Recently Zoherevand and Mirmiran [9] studied the seismic response of hybrid column made of a FRP tube filled with UHPC. The maximum ground acceleration capacity of five UHPC-filled FRP tubes and one reference concrete column was estimated based on the pseudo-static test. The results showed 20% higher maximum ground acceleration capacity for the UHPC-filled FRP tube, as compared to its reference concrete column counterpart.
However, more than a decade of studies on UHPC, few research are available about the behaviour of FRP confined UHPC columns under monotonic loading that contained no conventional reinforcement, either in the longitudinal or transverse direction. Moreover, no research data has been published dealing with steel-reinforced UHPC columns confined by FRP and subjected to P-M loading. To this end, the present research is aimed to investigate and understand the performance of steel-reinforced FRP tubular columns in filled with UHPC under P-M loading, in addition to provide valuable data that would aid to develop a design model for FRP confined UHPC columns under P-M loading. The experimental results of this research are compared against theoretical P-M interaction diagrams as well.
Experimental Investigation
Test specimens and material properties
In this study, eight steel reinforced UHPC column specimens were tested consisting of five specimens had FRP tube (one specimen under concentric loading, three specimens under eccentric loading of 10 mm, 85 mm and 95 mm, and one specimen under pure bending that is, an eccentricity approaching infinity) and another three unconfined columns considered as references (one specimen under concentric loading and two specimens under eccentric loading of 10 mm, 85 mm). All the column specimens had square cross sections, with UHPC core dimensions 140 mm by 140 mm and a height of 840 mm for concentric and eccentric loading specimens and 1200 mm for pure bending specimen. The longitudinal steel reinforcement are consisted of four deformed steel bars N16 and Grade 500 MPa which corresponded to a steel reinforcement ratio of about 4% for all specimens. The shear reinforcement consisted of 6 mm diameter plain wire ties spaced at 100 mm on center and the clear concrete cover was 20 mm. The specimens were confined by formerly manufactured FRP tubes. These tubes were prepared using a manual wet layup process by wrapping epoxy resin-impregnated fiber sheets around precision-cut high-density Styrofoam templates in the circumferential direction. An overlap length of 150 mm was provided in all specimens to prevent premature debonding failure. Specimens confined with 4 layers of FRP were wrapped with two FRP sheets, and hence had one overlap regions. The specimens were labelled as XUHPC-Y, for the UHPC column where X represents (confined or unconfined) column with FRP and Y represents an initial load eccentricity recorded in (mm). The details of the test column specimens are given in Table 1 and Figure 1 and the materials properties are provided in Table 2.
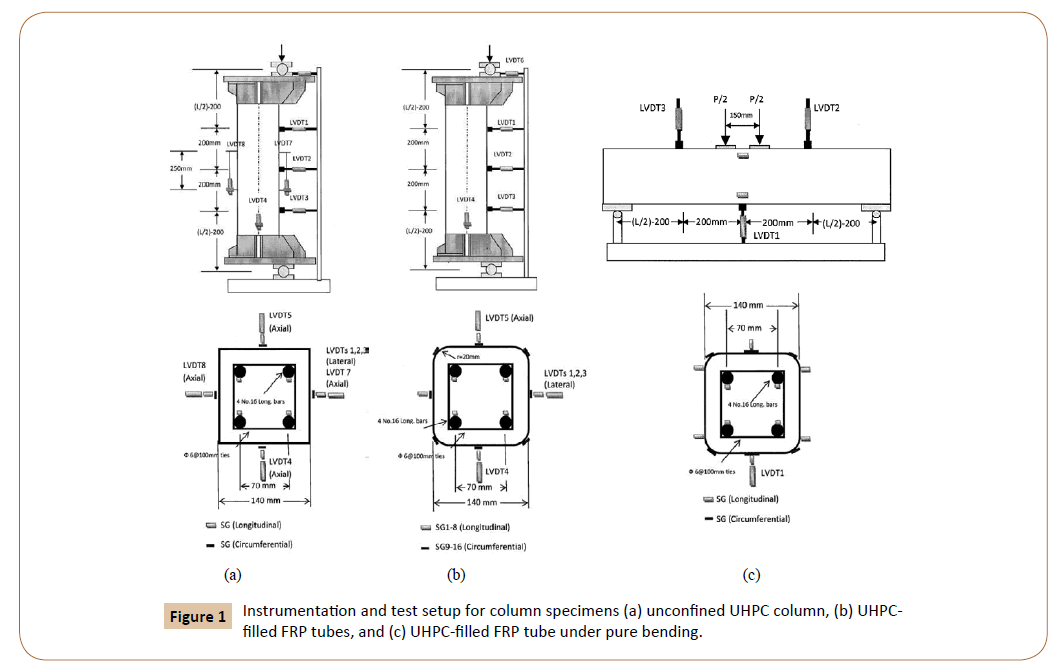
Figure 1: Instrumentation and test setup for column specimens (a) unconfined UHPC column, (b) UHPCfilled FRP tubes, and (c) UHPC-filled FRP tube under pure bending.
Table 1: Details of the test column specimens.
| No. | Specimens label | FRP layers | Eccentricity, emm |
|---|---|---|---|
| 1 | UHPC-0 | 0 | 0 |
| 2 | UHPC-10 | 0 | 10 |
| 3 | UHPC-85 | 0 | 85 |
| 4 | CUHPC-0 | 4 | 0 |
| 5 | CUHPC-10 | 4 | 10 |
| 6 | CUHPC-85 | 4 | 85 |
| 7 | CUHPC-95 | 4 | 95 |
| 8 | CUHPC-PB | 4 | ∞ |
Table 2: Results of ancillary testing for constituent material properties.
| Material | Property | Average | # of tests |
|---|---|---|---|
| UHPC | 28-day compressive strength (MPa) | 150 | 18 |
| Axial strain at failure (%) | 0.5 (a) | 5 | |
| Split tensile strength (MPa) | 19.3 | 13 | |
| Flexural tensile strength (MPa) | 21.1 | 6 | |
| UHPC confined with FRP | 28-day compressive strength (MPa) | 218 | 3 |
| Avg. axial strain at failure (%) | 1.7(a) | 3 | |
| Avg. hoop strain at failure (%) | 0.36(b) | 3 | |
| Reinforcing steel | Yield strength (MPa) | 576 | 3 |
| Ultimate strength (MPa) | 642 | 3 | |
| Elastic modulus (GPa) | 202 | 3 | |
| FRP sheets(c) | Type | Carbon-High Modulus | |
| Nominal thickness, tf (mm/ply) | 0.19 | 3 | |
| Tensile strength, ffu (MPa) | 3265 | 3 | |
| Ultimate tensile strain, εfu (%) | 0.36 | 3 | |
| Elastic modulus, Ef (GPa) | 657 | 3 |
a) Average of 6 axial SG and 12 LVDTs readings (two SG and four LVDTs on each cylinder).
b) Average of 9 hoop SG and 9 LVDTs readings (three SG and three LVDTs on each cylinder).
c)Obtained from flat FRP coupon tests and calculated based on nominal thickness of fibers.
Test matrix
The mix design was developed by a previous research study at the school of Civil, Environmental and Mining Engineering, University of Adelaide [10]. The UHPC was mixed using locally available materials: 940 kg/m3 of sulfate resisting cement, 470 kg/m3 of silica sand 60G (average size 50 μm), 470 kg/m3 of silica sand 30/60 (average size 400 μm), 250 kg/m3 of undensified silica fume, and 164.5 kg/m3 of steel fibers with volume fraction (Vf) of 2.25%. The steel fibers used were hooked-ends steel fibers 35 mm long, 0.55 mm in diameter, and had an ultimate tensile strength of 1100 MPa. High-range water-reducing admixture Sika Viscocrete 5-500, was used in the current study and the water-binder ratio (w/b) was 0.15. All of the dry constituents of the UHPC were batched by an electronic balance and mixed in a horizontal pan mixer for 3 minutes. Water and super-plasticizer mixed together and added gradually to the dry materials, until the materials were uniformly mixed. Then the fibers were introduced and mixed for additional 5 minutes. The flow of this mix was 190 mm.
The hollow FRP tubes were placed in a vertical position on a wooden frame then the steel reinforcements fixed inside the FRP tubes as shown in Figure 2a. The columns were cast vertically with one column specimen cast from each batch. To prevent fiber segregation, the UHPC was compacted using a vibrating table. After casting, all of the columns and control specimens were covered with wet Hessian and plastic sheet for 24 hours. All specimens were then stripped and cured in the fog room under a certain controlled temperature (24°C) until age of 28 day. The testing of the UHPC-filled FRP tube specimens, unconfined UHPC column and the control specimens of UHPC started right after the attainment of the 28-day strength and continued for approximately 4 weeks.

Figure 2: (a) The moulds of FRP tubes, (b) rigid steel cap, (c) test setup for specimen under concentric loading, (d) test setup for specimen under pure bending and (e) test setup for specimen under eccentric loading (images by Maha Ridha).
Test set-up and Instrumentation
The column specimens under eccentric loading were tested using a specially design loading system similar to that used by Fam et al. [11] and Malik et al. [12], with a unique modification, to apply a coupled axial load and bending moment. The loading device, which was designed by the author especially for the current study, consisted of 160 mm square rigid steel caps placed over the ends of the columns and (hinge) included steel rollers which were nested in the semi-circular grooves in opposing end plates. The interior dimensions of the steel caps have been designed to be fixed by welding from one side and changeable from the other side by using elliptical bolts slots. The hinge was used to set the load eccentricity within required value for each test. The hinge plate fixed over the steel cap plate by cap head screws [11,12]. Figure 2b and 2e show the details of rigid steel cap. All the column specimens under concentric and eccentric loading were tested using a 5000 kN-capacity Amsler testing machine, whereas the pure bending specimen was tested using a 1000 kNcapacity Avery testing machine.
For the eccentric loading UHPC-filled FRP tubes and unconfined UHPC columns, the specimens were tested to failure under eccentric load with eccentricity of 0, 10, 85 and 95 mm. The lateral displacement measurements were taken at column midheight and 200 mm above and below mid-height using three linear variable differential transducers (LVDTs). Axial deformation was recorded using two LVDTs over a gauge length of 700 mm as shown in Figures 1a, 1b and 2e. The column specimens were instrumented to measure axial compressive strains and transverse fiber strains. After cleaning and preparation of the specimen surface, the strain gauges (SG) were attached to the column surface at mid-height using a strain gauge adhesive. For each UHPC-filled FRP tubes, four electrical strain gauges with a gauge length of 20 mm were placed in the longitudinal direction and eight strain gauges with a gauge length of 30 mm were placed in transverse direction on the sides and corners to measure axial and circumference strains at mid-height, respectively as shown in Figure 1b.
For unconfined UHPC columns, four electrical strain gauges with a gauge length of 20 mm were placed in the longitudinal direction and four strain gauges with a gauge length of 30 mm were placed in transverse direction on the sides to measure axial and circumference strains at mid-height, respectively. Also two LVDTs were installed on compressive and tensile sides over a gauge length of 250 mm at mid-height to record axial deformations as shown in Figure 1a.
For pure bending test of UHPC-filled FRP tube, the specimen was tested to failure under four-points loading with an effective span of 1100 mm and a shear span of 475 mm. The deflection was monitored by three LVDTs mounted at mid-span and at 200 mm from mid-span at each side as shown in Figures 1c and 2d. Four electrical strain gauges with a gauge length of 20 mm were placed in the longitudinal and transverse directions on top and bottom faces of mid-span of beam specimen to measure the compressive and tensile strains. Again, transverse strains were measured on the corner at the mid-span. For all the specimens, four electrical strain gauges with a gauge length of 6 mm were placed on the longitudinal steel reinforcement at mid-height or span to record axial strains. A variety of additional tests were carried out on the constituent materials of columns as shown in Table 2, including:
1. FRP confined unreinforced UHPC cylindrical specimens (100 mm diameter and 200 mm length) under uniaxial compression tests (identical to the compression test method of Ozbakkaloglu's [13] as shown in Figure 2c, to determine the characteristics of the confined stress– strain behavior).
2. Unconfined UHPC cylindrical specimens (100 mm diameter and 200 mm length) under uniaxial compression tests.
3. Split tensile tests of UHPC cylinders (100 mm diameter and 200 mm length).
4. Flexural tensile tests of (100 mm square cross section and 500 mm length) UHPC 4-points loading unnotched prisms.
5. Tensile tests on steel reinforcement.
Experimental Results and Discussion
Based on the experimental results in Table 3, axial load carrying capacities, Pmax, decreased as the initial load eccentricity, e, increase. This is due to the fact that the benefits of FRP confinement at Pmax are less pronounced for large initial load eccentricities [14,15]. For specimens tested under 0, 10 mm and 85 mm eccentricities, UHPC-filled FRP tubes had only 5.9%, 3% and 2.3% larger axial load carrying capacities than unconfined UHPC specimens, respectively, whereas the axial displacement capacities were 67.7%, 63.5% and 32.6% greater than unconfined UHPC specimens for CUHPC-0, CUHPC-10 and CUHPC-85, respectively. This is attributed to the FRP confinement effectiveness in increasing the column strength is significantly less for ultra-high strength concrete compared with conventional strength concrete [16,17].
Table 3: Experimental results of tested specimens.
| Specimen | Pmax., (kN) | Initial load eccent., e (mm) | Lateral disp. At max. load,1 (mm) | Axial disp. At max. load δ (mm) | Moment, (kN.m) | Lateral disp. At failure load2 (mm) | Mode of failure | |
|---|---|---|---|---|---|---|---|---|
| M1=Pmax*e | M2=Pmax(e+1) | |||||||
| UHPC-0 | 3155 | 0 | ---- | 1.89 | ---- | ----- | ---- | Compression |
| UHPC-10 | 2856 | 10 | 1.68 | 1.59 | 28.56 | 33.36 | 1.68 | Compression |
| UHPC-85 | 572 | 85 | 7.91 | 0.92 | 48.54 | 53.05 | 8.92 | Compression |
| CUHPC-0 | 3340 | 0 | ---- | 3.17 | ----- | ----- | ---- | Compression |
| CUHPC-10 | 2945 | 10 | 2.69 | 2.6 | 29.45 | 37.35 | 13.11 | Compression |
| CUHPC-85 | 584 | 85 | 9.79 | 1.22 | 49.68 | 55.38 | 48.5 | Balanced |
| CUHPC-95 | 473 | 95 | 10.5 | 1.7 | 44.98 | 49.95 | 46.7 | Tension |
| CUHPC-PB* | 148 | ---- | 14.2 | ---- | 35.15 | 91.8 | Pure bending | |
*Specimen CUHPC-PB was loaded flexurally, therefore lateral displacement is in the direction of loading and M=Pmax.(a/2), where a=shear span of the specimen.
For cylindrical specimens, including unconfined UHPC and UHPCfilled FRP tube, the compressive strength test results show that under concentric compressive load, the ultimate strength of the 150 MPa UHPC was increased by about 45% due to FRP confinement and the axial strain at failure was greatly increased by 240% on average due to FRP confinement. The average circumferential strain in the FRP at failure was around 0.36%, which is identical to the average failure strain recorded in direct tensile tests on FRP coupons.
However, Zohrevand and Mirmiran [18] have recently used the results of sixteen FRP confined and three unconfined UHPC cylindrical specimens under uniaxial compression test to recalibrate the two commonly used FRP confinement stressstrain models of Samaan et al. [19] and Lam and Teng [20]. This led Zohrevand and Mirmiran [18] to conclude that the recalibrated model of Saman is more accurate and easier to use as compared to other models, so it is proposed as a suitable model for FRPconfined UHPC. Based on this model and with inclusion of a reduction factor ψf=0.95, based on the specifications of ACI 440. 2R-08 [21] (committee’s judgment) , the predicted compressive strength and ultimate axial strain of the current study increase by 97% and 20%, respectively, (assuming that the full tensile strength of the FRP is achieved at ultimate), which are not dramatically close with the experimental results. This scatter between the experimental and predicted results indicates that the proposed model of Zohrevand and Mirmiran [18] is inefficient enough for quantify the increase in strain and strength capacity of FRP confined UHPC due to the limited data available on FRP confined UHPC, therefore, further research is required to recalibrate and improve the model efficiency. The material properties given in Table 2, the stress-strain model of Zohrevand and Mirmiran [18] and ACI 440. 2R-08 [21] specifications have been used below in the development of theoretical P-M interaction diagrams for UHPC-filled FRP tubes.
Moment capacity and lateral deformation
Figure 3 shows the effect of the load eccentricity on the behaviour of UHPC-filled FRP tubes and unconfined UHPC columns, which is represented by the curves of applied moment (M2) versus midheight lateral displacement (Δ) of specimens with eccentricities of (10, 85 and 95) mm and infinity (pure bending). Therefore, the following observations can be reported:
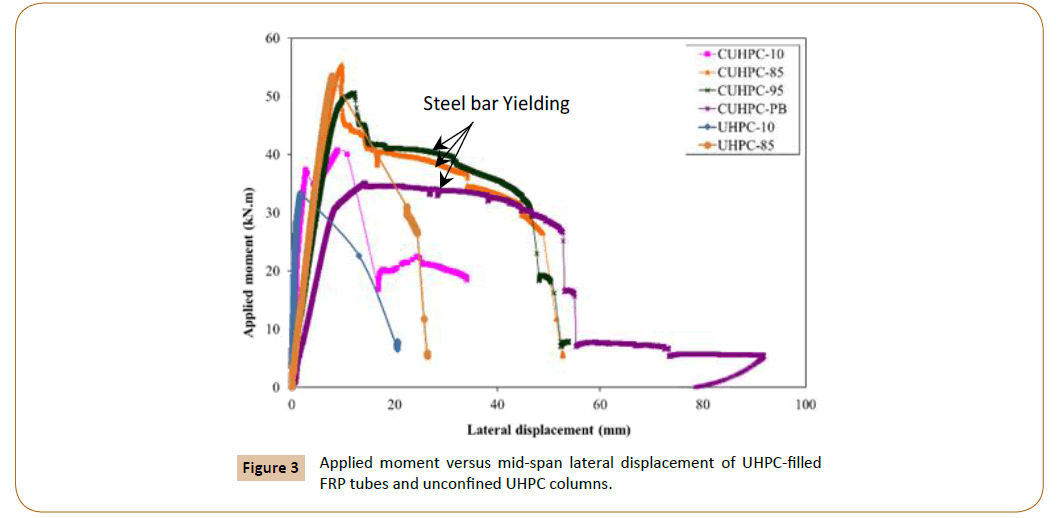
Figure 3: Applied moment versus mid-span lateral displacement of UHPC-filled FRP tubes and unconfined UHPC columns.
1. For the UHPC-filled FRP tubes, the flexural stiffness (which is represented by the slope of the curve) increased as the eccentricity decreased due to the effect of the axially applied load location.
2. For the same initial load eccentricity columns (e=10 mm and 85 mm), corresponded flexural stiffness for the UHPC-filled FRP tubes and the unconfined UHPC columns. However, the UHPC-filled FRP tubes achieved higher moment capacity (M2), lateral displacement at maximum load (Δ1) and lateral displacement at failure (Δ2) than the unconfined columns by 12%, 60% and 680%, respectively for eccentricity 10 mm and by 4.4%, 24% and 444%, respectively for eccentricity 85 mm, which indicates that the significant ductility has been achieved by using FRP confinement.
3. Given the applied moment, the UHPC-filled FRP tubes with lower eccentricities featured less lateral displacement at the first stages of loading and exhibited substantially large lateral displacements beyond the yielding stress of tension steel reinforcement for the specimens with initial load eccentricities of 85, 95 and ∞ (infinity) mm.
4. Specimen CUHPC-10, with an initial load eccentricity of 10 mm, also shows good ductility even though the tension steel reinforcement did not yield.
Failure modes
Figure 4 shows the different failure modes for the tested UHPCfilled FRP tube and unconfined column specimens. For the specimen CUHPC-PB, the failure was by FRP tube rupture in the tension side within the constant moment region in the transverse direction followed by yielding of tensile steel (flexural failure). This mode of failure was a similar fashion to the eccentrically loaded column specimen CUHPC-95 that failed in tension, as shown in Figure 4d. The axial strain measured on the compression side of the tubes of specimen CUHPC-PB was less than 0.4% at Pmax, (with no sign of compression damage). On the other hand, the axial tensile strain was not reported due to malfunction of instrument during testing. Eccentrically loaded column specimens failed either in compression or tension, depending on the eccentricity of the applied load as shown in Figure 4a and 4c. Generally, for the tests conducted on FRP confined column specimens, when the FRP fibres began to stretch near the peak load, several snapping sounds were heard, however, there were no visible signs of any damage on the surface of the FRP tube For the column specimens CUHPC-0 and CUHPC-10 , failure occurred when the FRP tube ruptured in tension and spilt vertically on the compressive side after concrete crushing at mid-height of the specimen without any yielding of tension steel (compression failure). Whereas specimen CUHPC-95 was failed by yielding of tension steel that followed by rupture of FRP tube in transverse direction (tension failure). Specimen CUHPC-85 had a balanced failure including rupture of the FRP tube in transverse direction after bursting of concrete, almost simultaneously with yielding of tension steel reinforcement as shown in Figure 4b.

Figure 4: Typical failure modes of UHPC-filled FRP tube specimens and unconfined UHPC columns.
For the test conducted on unconfined column specimens UHPC-0 and UHPC-10, it was shown that as the loading increased, further cracks formed and propagated through the depth of the section. Then, the cracks moved upward and downward towards the pin point of LVDT on the compressive side where as weak points acted and facilitated the propagation of the cracks. The failure occurred suddenly by crushing of concrete at the compression side and at the two sides of column without yielding of tension steel reinforcement (compression failure) and cracking sounds could be heard clearly near and at Pmax. Figure 4d shows the failure pattern of specimen UHPC-10. It is clear from this figure that while significant crushing of the concrete was observed, there were no signs of cover spalling even beyond the peak loading.
Axial and circumferential strains
For the discussion purposes, Figure 5 compares the load versus axial strain behaviour at the mid-heights of (a) unconfined UHPC column and UHPC-filled FRP tube with 10 mm initial load eccentricities and (b) UHPC-filled FRP tubes with 10 mm, 85 mm, 95 mm and ∞ initial load eccentricities. Figure 6 provides a similar comparison for circumferential strain data for UHPC-filled FRP tubes with 10 mm, 85 mm, and 95 mm initial load eccentricities, and pure flexural loading. Whereas Table 4 provides a complete summary of average and maximum axial compressive strain and circumferential strain values readings recorded at maximum axial load and at failure for all specimens tested in the current study.
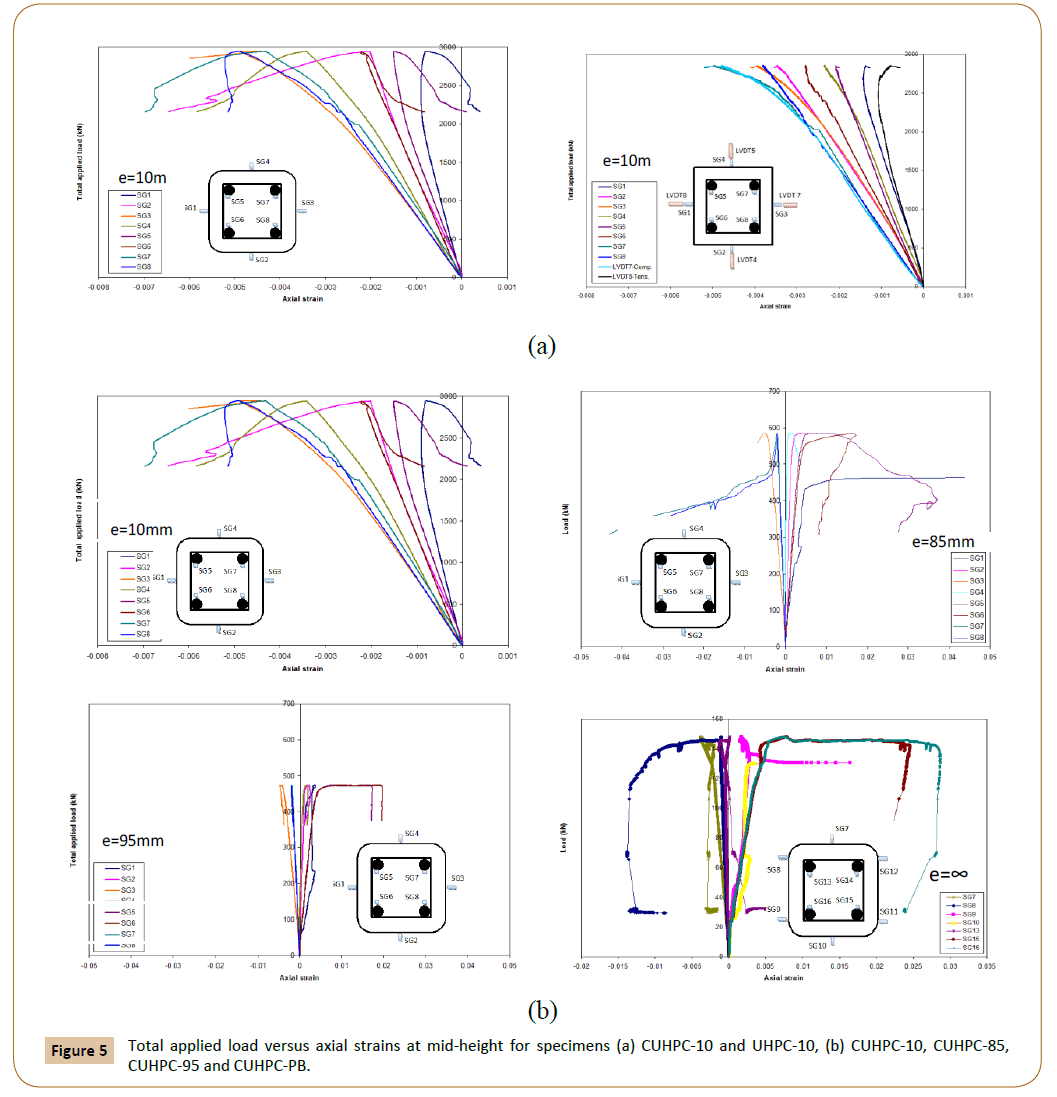
Figure 5: Total applied load versus axial strains at mid-height for specimens (a) CUHPC-10 and UHPC-10, (b) CUHPC-10, CUHPC-85, CUHPC-95 and CUHPC-PB.
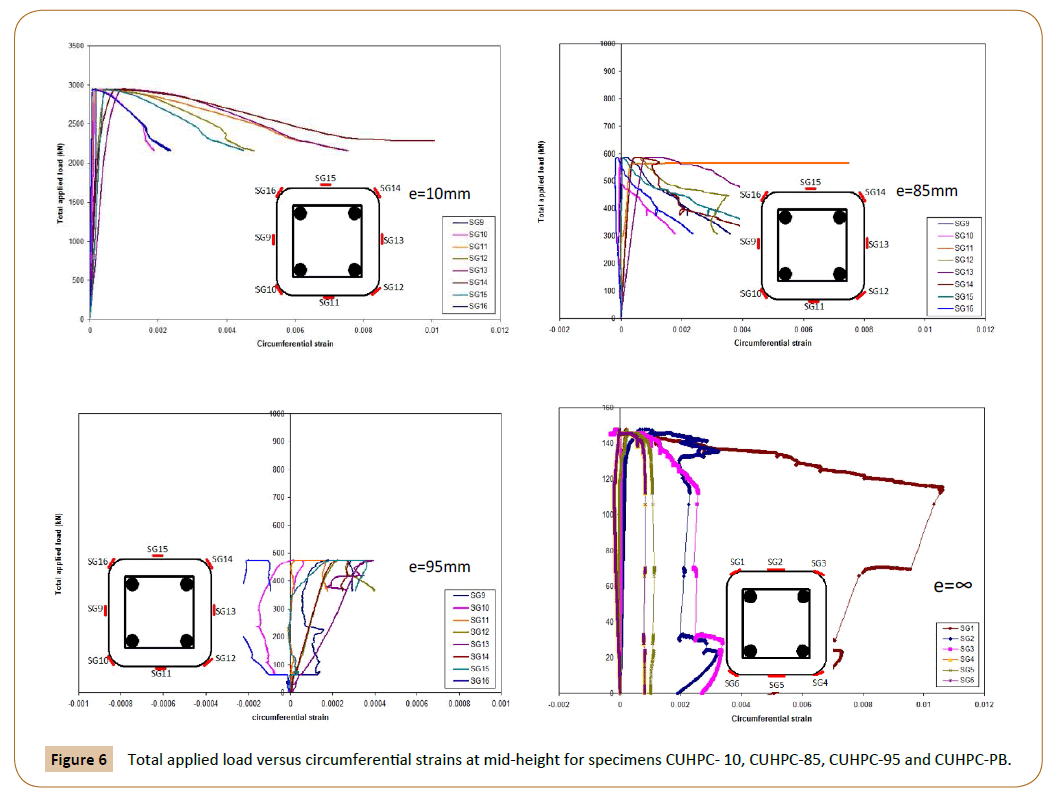
Figure 6: Total applied load versus circumferential strains at mid-height for specimens CUHPC- 10, CUHPC-85, CUHPC-95 and CUHPC-PB.
Table 4: Summary for average and maximum axial compressive strain and circumferential strain values for all specimens.
| Specimens | Pmax. (kN) | Avg. axial strain at max. load (%)* | Max. axial at max. load (%) | comp. strain | Avg. circumf. strain at max. load (%)** | Max. circumf. strain at max. load (%) | Avg. circumf. strain at failure (%) | Max. circumf. strain at failure (%) |
|---|---|---|---|---|---|---|---|---|
| UHPC-0 | 3155 | -0.31 | 0.56 | --- | --- | --- | --- | |
| UHPC-10 | 2856 | -0.25 | 0.48 | --- | --- | --- | --- | |
| UHPC-85 | 572 | 0.22 | 0.51 | --- | --- | --- | --- | |
| CUHPC-0 | 3340 | -0.46 | 0.61 | 0.0425 | 0.123 | 0.0441 | 0.134 | |
| CUHPC-10 | 2945 | -0.3 | 0.5 | 0.0381 | 0.0994 | 0.0389 | 0.105 | |
| CUHPC-85 | 584 | 0.31 | 0.53 | 0.0246 | 0.0745 | 0.0257 | 0.083 | |
| CUHPC-95 | 473 | 0.058 | 0.44 | 0.0124 | 0.0353 | 0.0129 | 0.039 | |
| CUHPC-PB | 148 | -0.22 | 0.4 | 0.0331 | 0.073 | 0.115 | 0.32 |
*Calculated as an average of all axial SGs at mid height of each specimen as shown in Figure 1. The negative signal means compression and the positive signal means tension.
**Calculated as an average of all circumferential SGs at mid height of each specimen as shown in Figure 1.
Figure 5a shows that the bending moments caused by the eccentric loading with initial load eccentricity 10 mm (e=0.07 h < 0.1 h) caused only axial compressive strains within the column cross-sections for UHPC columns with and without FRP tubes, which considered as an indication that the behaviour of UHPC columns is compatible with the ACI 440.2R-08 [21] requirement for conventional concrete columns. Whereas Figure 5b shows that the bending moments caused by the eccentric loading were sufficient to cause both axial tensile and axial compressive strains within the specimen cross-sections in UHPC-filled FRP tubes with initial load eccentricity 85 and 95 mm. The load versus axial strain data for SG2 and SG4 in Figures 5a and 5b shown an indication for small deviation between locations of theoretical flexural parity within the cross-sections for all UHPC columns with and without FRP tubes, except column CUHPC-95, which refers to the small inadvertent biaxial bending which was probably because of slight misalignment of the load collars or small defects resulting during fabrication.
The load versus axial strain curves for the UHPC-filled FRP tubes showed the distinctive bi-linear shape in a secondary ascending branch, and typically occurred after the most compressed region of the cross-section had reached an axial strain of around (0.4- 0.45%), which is in the range of the strain at peak stress for unconfined UHPC, as expected. For concentrically-loaded UHPCfilled FRP tube cylinders, 0.4% is typically the axial strain level after which extensive micro-cracking of the confined UHPC occurs, causing accelerating dilation and activating of the FRP tube. The bi-linear transition became less obvious with increasing initial load eccentricity such as column CUHPC-95 (which failed in tension). For pure bending specimen CUHPC-PB, the load versus axial strain curves showed a bi-linear shape in some descending branches as shown in Figure 5b.
Table 4 provides average and maximum axial compressive strain values for all specimens. For UHPC-filled FRP tubes CUHP-0, CUHPC-10, CUHPC-85 and CUHPC-95 (the average was calculated from four strain gauges at mid-height, as shown in Figure 1b, whereas for unconfined columns UHPC-0, UHPC-10 and UHPC- 85 (the average was calculated from four strain gauges and two LVDTs at mid-height, as shown in Figure 1a and for pure bending specimen CUHPC-PB (the average was calculated from just three strain gauges 7, 8 and 9 at mid-height due to malfunction of other strain gages during the test, as shown in Figure 1c. At Pmax., the average and max. axial compressive strains for specimens UHPC-0, UHPC-10, UHPC-85, CUHPC-0, CUHPC-10 and CUHPC-85 shown there are no significant improvement from using FRP tube confinement with UHPC columns for an initial load eccentricity 0, 10 mm and 85 mm, where the max. Load increased 5.9%, 3% and 2.1% respectively, and the max. Axial compressive strain increased 8.9%, 4% and 3.9% respectively, by using FRP tube confinement. This behavior contrasts with the behavior of normal strength concrete columns at low load eccentricities, which show the significant benefits of confining pressure in enhancing the deformability of concrete [14], (for example, Bisby and Ranger [15] tests conducted that FRP confinement for normal strength concrete column under an initial load eccentricity 10 mm increasing the max. load and max. axial compressive strain around 26.4% and 48.5%, respectively, over than the unconfined normal strength concrete column under the same initial load eccentricity). No obvious trend is apparent in the average and maximum axial strain data for the UHPC-filled FRP tubes, except to note that there is a change in the signals of average axial strain were changed from negative signal (compression) in column CUHPC-0 and CUHPC-10 to positive signal (tension) in columns CUHPC-85 and CUHPC-95, due to the diversity in the failure modes of those columns. It is clear from Figure 6 that the strain gradient resulting from the eccentric loading and by increasing secondary moments M2 for columns CUHPC-0, CUHPC-10, CUHPC-85 and CUHPC-95, produced different circumferential confinement of the column cross-sections. Indeed, Figure 6 shows highly variable confinement that resulted from the axial–flexural loading, where the tensile circumferential strains were highest near the extreme compression fibre and lowest at the least compressed fibre, because dilation and confinement were most activated near the extreme compression fibre [22]. Table 4 indicates that the average circumferential strains at peak load (calculated as the average of eight circumferential-direction readings for each column) in general decreased with increasing initial load eccentricity. Also it is interesting to note that the average circumferential strains at failure were slightly higher than at peak load for the eccentric loading columns CUHPC-0, CUHPC-10, CUHPC-85 and CUHPC-95, in contrast it was significantly higher for pure flexural loading CUHPC-PB, where flexure dominated the response. Furthermore, Table 4 displayed the maximum circumferential strains at peak load and at failure for all UHPC-filled FRP tube columns, these data show similar trends to the average circumferential strain values, where typically tend to decrease with increasing initial load eccentricity. The maximum recorded circumferential strains in the FRP tubes were typically less than the ultimate tensile strain of tested coupon 0.0036 (Table 2). In one case however (Specimen CUHPC-PB), the maximum circumferential strain at failure, which recorded in SG1, strain gage no.1, (Figure 6) was significantly higher than that determined from coupon tests. This may be attributed to the known spatial variation in circumferential strains over the surface of an FRP tube which confined a square cross-section specimen at loads near ultimate [23].
P-M Interaction Diagram
To draw a P-M interaction diagram for UHPC-filled FRP tube specimens by using sectional analysis procedures, it is important to use a stress-strain curve based on concentrically-loaded UHPC-filled FRP tubes. This central assumption, in addition to the following assumptions is considered for the analysis of the current study:
a. Plane sections remain plane before and after bending.
b. The tensile strength of UHPC is neglected,
c. The confinement provided by the column’s ties is neglected, and
d. Perfect bond is assumed between both steel reinforcement bar-UHPC and FRP tube-UHPC.
The validity of these assumptions is confirmed later by comparing the analytical results with the experimental results.In the following sections, P-M interaction diagram are developed for the UHPC-filled FRP tube specimens tested in the current study by using sectional analysis procedure in conjunction with a stress-strain relationship of the UHPC-filled FRP tubes developed by Zohrevand and Mirmiran [18] that based on a commonly used FRP-confined conventional concrete model for Samaan et al. [19], and also by using some of the design limitations that has been recommended by ACI 440. 2R-08 [21] and ACI 318-14 [24].
Analytical model
The sectional analysis procedure is covered in detail in most reinforced concrete design texts [25] and several research [11,26,27], so no need to present in detail here. In the current study, The reinforced steel stress-strain relationship in compression and tension is modelled to be linear elastic-plastic with a post-yield strain hardening of 1% [28,29], based on data from tensile tests performed for the current study. For the FRP composite the stress-strain relationship is modelled to be linear elastic up to failure and the ultimate tensile strength is taken as the average value from FRP coupon tests performed for the current study as shown in Table 2. The FRP-confined UHPC stressstrain relationship developed by Zohrevand and Mirmiran [18] is illustrated in Figure 7 and described by equations (1)- (12).

Figure 7: Schematic Stress-Strain Model of Samaan [17].
The FRP-confined UHPC compressive strength and the corresponding maximum strain, f'cu and ÆÂÂÂÂcu , respectively, are given by the following equations:
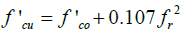 (1)
(1)
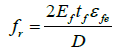 (2)
(2)
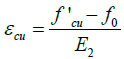 (3)
(3)
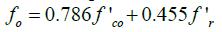 (4)
(4)
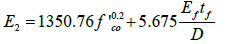 (5)
(5)
Where, f'co=unconfined UHPC compressive strength, fr=confinement pressure due to FRP tube,
Ef=tensile modulus of elasticity of FRP, tf=the tube thickness, D=the core diameter, which is equal to  for noncircular cross section [21], fo=the intercept stress that specified as a function of the strength of unconfined UHPC and the confining pressure developed by FRP tube and εfe=FRP effective strain, (strain level reached at failure). In order to ensure the shear integrity of the confined concrete, the effective strain in the FRP at failure εfe in members subjected to combined axial compression and bending moment should be limited as eqn. (6), based on the work by Priestley et al. [30] and as recommended by ACI Committee 440.2R-08 [21].
for noncircular cross section [21], fo=the intercept stress that specified as a function of the strength of unconfined UHPC and the confining pressure developed by FRP tube and εfe=FRP effective strain, (strain level reached at failure). In order to ensure the shear integrity of the confined concrete, the effective strain in the FRP at failure εfe in members subjected to combined axial compression and bending moment should be limited as eqn. (6), based on the work by Priestley et al. [30] and as recommended by ACI Committee 440.2R-08 [21].
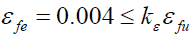 (6)
(6)
Where, εfu=FRP ultimate tensile strain and kε=FRP strain efficiency factor. The FRP strain efficiency factor kε represents the difference between the actual circumferential rupture strain observed in FRP-confined concrete specimens and FRP material rupture strain computed from tensile coupon testing. An average value of 0.58 was computed for kε by Lam and Teng [20] and Gary and Harries [31], based on experimental calibration using CFRP-confined concrete specimens. Whereas, Ozbakkaloglu's [13] experimental tests on FRP-confined ultra-high strength concrete specimens resulted in value of 0.57, which has been used in this study to draw P-M interaction diagram (theoretical P-MS2). The results are compared with the P-M interaction diagram (theoretical P-MS1) as shown in Figure 8, by using the parameter εfe equal to 0.004 (identify to the FRP ultimate tensile strain which provided by manufacturer) based on ACI Committee 440 limitation in eqn. (6). Finally, the ACI Committee recommends that the ultimate uniaxial compressive strain of the FRP-concrete, ÆÂÂÂÂcu, should not be taken greater than 1.0% “to prevent excessive cracking and the resulting loss of concrete integrity”.
The bilinear response of FRP-confined UHPC represented by using a single equation as:
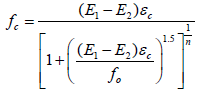 (7)
(7)
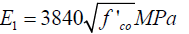 (8)
(8)
Where, fc and ÆÂÂÂÂc=the axial stress and strain of FRP-confined UHPC, respectively, E1=the Young's modulus of UHPC [32] and n=the parameter for the curvature of the transition zone which was selected as 12 by Zohrevand and Mirmiran [18].
According to the requirements of ACI 440.2R-08 [21] and ACI318- 14 [24] , the nominal axial load Pn of an reinforced concrete column featuring ties as steel transfers reinforcement, can be found using eqn. (9) when the eccentricity present in the member is less than or equal to 0.1 h, (Mn equals zero). The strength reduction factor φ is 0.65 due to that the interaction diagram corresponds to compression controlled members and the 80% is an additional reduction factor for a possible accidental eccentricity [26].
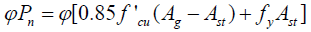 (9)
(9)
The nominal axial load Pn and the nominal bending moment Mn can be found by integration of the stresses over the cross-section by using eqns. (7) and (12).
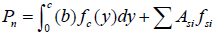 (10)
(10)
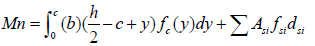 (11)
(11)
Where, c=the distance from the neutral axis position to the extreme compression fiber in the cross-section. y=the variable of integration within the compression zone. fsi and Asi=the normal stress and the cross-sectional area of the (ith) layer of longitudinal steel reinforcement, respectively. dsi=the distance between the position of the (ith) layer of longitudinal steel reinforcement to the geometric centroid of the cross-section. The concrete stress fc is computed by using eqn. (7) that corresponds to the stressstrain curve model by Zohrevand and Mirmiran [18]. The strain at any distance y from the neutral axis is given by:
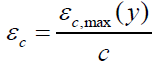 (12)
(12)
At failure, u for a FRP-confined UHPC. The value of is given by eqn. (3).
The nominal bending moment Mn, for the pure bending moment case (zero axial load) can be found by assuming no contribution of the FRP-confinement for the flexural capacity of the specimen, where specimen featured FRP tube with unidirectional fibers in the transverse direction. The neutral axis position is obtained by following conventional beam theory [21,33].
To test the theoretical results for P-MS1 interaction diagram, the relative values of axial load and bending moment RV (Pexp./ Ptheo. or Mexp./Mtheo.) were found for the 5 UHPC-filled FRP tube specimens in this research work, then the mean (μ), standard deviation (SD), and the coefficient of variation (COV) were calculated for these results as shown in Table 5.
Table 5: Comparison of experimental and theoretical results for UHPC-filled FRP tube specimens under concentric loads, eccentric loads and pure bending.
| Specimens | Experimental axial load (kN) | Theoretical axial load for P-MS1 | Experimental bending moment (kN.m) | Theoretical bending moment for P-MS1 diagram (kN.m) | RV |
|---|---|---|---|---|---|
| CUHPC-0 | 3340 | 3219 | 1.04 | ||
| CUHPC-10 | 2945 | 2402 | ------ | ---- | 1.22 |
| CUHPC-85 | 584 | 491 | ----- | ----- | 1.18 |
| CUHPC-95 | 473 | 400 | ----- | ----- | 1.18 |
| CUHPC-PB | ----- | ----- | 35.15 | 30 | 1.17 |
| (μ)=1.158 | |||||
| (SD)=0.0687 | |||||
| (COV)=0.059 |
Comparison with experiments
Figure 8 shows a comparison of P-M test data obtained from the current study (for initial eccentricity moments M1 and secondary moments M2) against diagrams calculated using a detailed sectional analysis procedure in conjunction with Zohrevand and Mirmiran confinement model [18] and some of the ACI 440. 2R- 08(21) and ACI318-14 [24] design limitations. Based on these limitations and Ozbakkaloglu's [13] conclusion, the strain limit εfe=0.004 was used in the theoretical P-MS1 diagram and the strain efficiency factor kε=0.57 was used in the theoretical P-MS2 diagram. However, for the columns under concentric loading, the strength reduction factor 80% for a possible accidental eccentricity in eqn. (9) was not considered in this study because the test was quite accurate to avoid the accidental load eccentricities. The both theoretical diagrams results are conservative. However, the theoretical P-MS1 diagram provide more reasonable agreement with the experimental data (COV=5.9%) than the theoretical P-MS2. The presence of steel fibers into ultra- high strength concrete (UHSC) columns is definitely act to improve the mechanical behavior of columns under concentric and eccentric loading such as crushing of concrete core, cover spalling, confinement, ductility and deformability[34]. Therefore, a combination between the effects of presence steel fibers and FRP confinement in UHPC columns create a complex state of stresses at the failure stages of columns. Thus the scatter between the experimental results and the predicted capacity of the theoretical P-MS1 diagram, reveals that the differences may have arisen from the insufficiency of Zohrevand and Mirmiran confinement model [18] to represent the stage of bilinear stressstrain behavior in columns which is reflected on the quantifying the increase in strength and strain capacity of UHPC-filled FRP tube under given loading conditions [34].
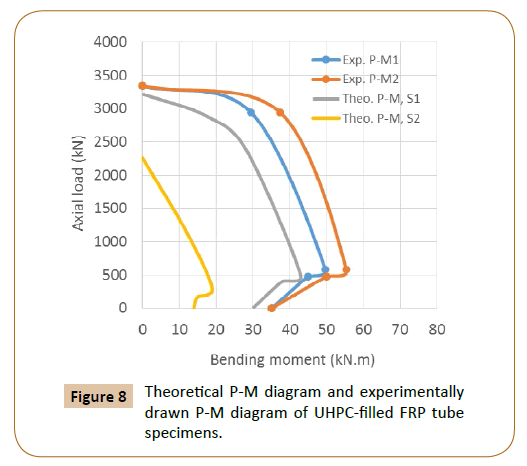
Figure 8: Theoretical P-M diagram and experimentally drawn P-M diagram of UHPC-filled FRP tube specimens.
When the experimental and theoretical values for the axial load carrying capacity of the specimens under concentric loads, eccentric loads and bending moment capacity of the specimen under pure bending are compared in Table 5, it can be seen that the proposed model gave reasonable prediction for the ultimate capacity of the UHPC-filled FRP tube specimens under concentric loads, eccentric loads and pure bending. Further experimental research for confined UHPC is needed to recalibrate the proposed model of Zohrevand and Mirmiran [18] and to find an accurate strain efficiency factors or strain limits for UHPC-filled FRP tube specimens with taking into consideration the combined effects of the presence of steel fibers in the concrete and the confinement by FRP.
Conclusions
In this study, a total of five UHPC-filled FRP tube specimens and three unconfined UHPC column specimens have been tested. The P-M interaction diagrams of UHPC-filled FRP tubes have been established experimentally and analytically. The following conclusions can be drawn on the experimental and analytical results of the study:
1. Comparing the strength and deformation capacity of the FRP confined column against identical unconfined column under eccentric axial loading refer that the significant ductility has been achieved by using FRP confinement. However, corresponded flexural stiffness for FRP confined column and unconfined column, the FRP confined columns achieved higher moment capacity, lateral displacement at Pmax., lateral displacement at failure and axial displacement at Pmax than the unconfined columns by 12%, 60%, 680% and 63.5%, respectively for eccentricity 10 mm and by 4.4%, 24%, 444% and 32.6%, respectively for eccentricity 85 mm.
2. The FRP confinement effectiveness in increasing the column strength is significantly less for UHPC compared with conventional strength concrete, where by using FRP tube confinement with UHPC columns for an initial load eccentricity 0, 10 mm and 85 mm the Pmax. Increased 5.9%, 3% and 2.1%, respectively, and maximum axial compressive strain increased 8.9%, 4% and 3.9% respectively, than unconfined UHPC columns.
3. Within the limits and conditions of this research, the proposed design procedure based on the conventional sectional analysis in conjunction with stress-strain model for concentrically loaded UHPC-filled FRP tube specimens provides conservative and reasonably well prediction of P-M interaction diagram for FRP confined UHPC columns (with COV=5.9%) when the maximum strain limit of ACI 440. 2R-08 (εfe=0.004) was used, and much highly conservative prediction of P-M interaction diagram for FRP confined UHPC columns when the strain efficiency factor (kε=0.57) was used.
Acknowledgements
The author would like to thank, and acknowledge the University of Technology and the University of Adelaide for supporting this research. The help provided from the University of AL-Mustansiria especially Associate Professor Dr. Nagham Al-shafi’i is much appreciated. The experimental work was financially supported by the University of Adelaide with a grant code: 15003450. The conclusions and recommendations presented here are those of the author and not necessarily those of the University of Technology or the University of Adelaide.