Research Article - (2015) Volume 23, Issue 5
Orthopedics and Traumatology Surgery, Alicante, Spain
Doctor of Pharmacy Program. University of Granada, Spain
Francisco Javier Carrera-Hueso Pharm D*
Pharmacy Service, Hospital Dr Moliner, Valencia, Spain
Pedro Vazquez-Ferreiro
Doctor of Pharmacy Program. University of Granada, Spain
PhD. Ophtalmologic Department. Hospital Virxen da Xunqueira, Cee, A Coruña, Spain
Diego Gómez-Herrero
Doctor of Pharmacy Program. University of Granada, Spain
Pharm. Head of Pharmacy Service. Hospital Nisa Rey Don Jaime, Spain
Jaime Eduardo Poquet-Jornet Pharm D
Head of Pharmacy Service, Alicante, Spain
Nuria Franco-Ferrando PhD
Head of Orthopedics and Traumatology Surgery, Hospital de Dénia Marina Salud, Alicante, Spain
María Auxiliadora Ramón-Barrios
Nurse, Pharmacy Service, Hospital Dr Moliner, Valencia, Spain
Our objective is to clinically validate two different pharmacoeconomics models for treating Dupuytren’s contracture (DC). We conducted a cross-sectional study to learn about orthopedists’ preferences regarding treatment for DC. A guided interview on two possible decision trees for treating DC was used. The attributes considered were: structural difficulty, comprehensibility, adaptability, reliability, extrapolation and applicability. The questionnaire was answered by 27 surgeons. The difference total score obtained was not statistically significant (t=1.523; P=0.14). No floor or ceiling affect was observed. The standard error of measurement was calculated at 0.796, being 8.0% with respect to the global for the scale. Minimal detectable change was 2.21. The total Cronbach’s alfa was high for both Models. The result of the principal analysis of the components explained 82.5% of the variation. Clinical validation of a pharmacoeconomic model for the management of DC has been shown to be feasible, flexible, and economical.
Dupuytren’s contracture, validity, pharmacoeconomic models, Delphi method, collagenase Clostridium histolyticum.
Every day more and more clinical validations of pharmacoeconomic models in use are carried out and reported, though the methods applied are not always indicated. The traditional manner for clinical validation in pharmacoeconomics has always been to gather opinions from clinical experts so that information about the models reflects all possible events, favorable or unfavorable, including secondary events.
Procedures that rely on the judgments of experts use techniques with different degrees of formality and employ qualitative methods for research and decision-making. These methods vary in the degree to which the panel of experts adopts norms that are formal, strict, and explicit for their interaction and communication in the process of arriving at a consensus. Among these methods we find consensus conferences, the RAND appropriateness method and the Delphi method.[1]
One of the most utilized techniques is the Delphi method, modified to more than one round or not, used to analyze the preferences of experts and achieve a proper clinical validation. This is a costly methodology since we all realize that the experts must devote a lot of time to making their judgments and reaching consensus.
Dupuytren’s contracture (DC) involves pathologic myofibroblast forming cords due to collagen deposits in the hand’s palmar fascia, which can result in fixed flexion deformity of the affected finger impairing normal hand function. Over time, this collagen may lead to metacarpophalangeal and/or proximal interphangeal joint contraction. Depending on the degree of contracture and the resulting deformity of the hand, a patient’s daily activities may become significantly affected as may his health-related quality of life, at which point he/she will often seek treatment.[2-4] Some of the factors implicated in the appearance and development of Dupuytren’s disease as supported by the greatest amount of scientific evidence include Northern European origin, hereditary factors, male gender, and smoking.
The traditional treatment option for DC has involved surgical removal or disruption of the fascial cord to allow release of the contracture. Although surgery is often effective in reducing the contracture, postoperative complications, such as nerve injury and wound healing problems are common, and patients usually experience contracture recurrence.[3]
An alternative nonsurgical treatment for DC is collagenase Clostridium histolyticum (CCH), which is injected directly into the cord to weaken it by enzymatic degradation, allowing the treating physician to manipulate and break the cord. Since its approval for marketing in Europe in February 2011, its use as an alternative treatment for DC has demonstrated the advantages of this non-invasive treatment (rapid recovery, low rate of complications and minimal skin alteration) over surgical treatment (eradication of the disease and a lower rate of recurrence). Its use has quickly spread throughout hand surgery units. The creation of infiltration and manipulation protocols in minor surgery operating rooms is allowing CCH infiltration to be gradually introduced as an alternative to fasciectomy, thus allowing for the optimization of both clinical and economic results for the center.[5]
Since the introduction of CCH on the market, it has been formally evaluated for effectiveness as compared with surgery in several studies. Chen et al. (6) used a simple decision tree to compare the results of surgical treatment with CCH for DC.
In Europe, there have not been any cost-effectiveness studies carried out such that would aid in the decision-making processes regarding treatment for DC. Therefore, we have attempted to use a more exhaustive pharmacoeconomic model that reflects all possible medical outcomes after treating the DC. To clinically validate our model, it must be compared with Chen’s model.[6]
The objective of our study is to clinically validate two different pharmacoeconomic models for treating Dupuytren’s contracture- one using fasciectomy and the other using collagenase. For this propose, we using a massive survey of experts in order to clinically validate a pharmacoeconomic model, as this should lower costs and be more flexible for researchers.
Study Description and Participants
We conducted a cross-sectional study to learn out about orthopedists’ preferences as to which decision model is best suited for treating DC.
We found 34 doctors willing to participate in the interview from among the orthopedists present at our hospital for Regional Meeting of Hand Surgery. They were given a guided interview on two possible decision trees for the treatment of DC. The first model was drawn from previous publications and the second model was designed by our team. Initially, one of the authors, RSC, explained to them the objective of our questionnaire, specifically, all possible health conditions obtained with each model and the differences between the two. [6,7] Participants were informed by RSC that if they did not want to continue their participation in the study, they could drop out any time they chose. Each and every one of the doctors verbally expressed his/ her desire to stay with the study.
The questionnaire that was distributed to the participants that same day considered six different attributes, one for each question. The attributes were: structural difficulty, comprehensibility, adaptability, reliability, extrapolation and applicability. All of the questions were written from the same positive perspective, so that results could be tallied without the necessity for any other adjustments. Answers were sorted using a quantitative 0 to 10 scale for each attribute and model under consideration. The doctors placed marks on the line at a point that they felt best represented their preferences, similar to a visual analog scale. Once the questionnaire was completed, the interviewer checked to make sure that the respondent had filled it out completely and that no data was missing.
The personal data that was collected from each participant included: initials, whether resident or a specialist, number of years spent in the specialty, and hospital affiliation. Confidentiality of the data was maintained at all times in accordance with current legislation.
The scoring and relevant data provided by the participants were introduced into a database previously prepared for the purpose using MS Excel 2007. The data were analyzed blindly such that it was not known a priori which specific model was being evaluated. We did not make any sample-sized calculations since we did have data available to us measuring the attributes studied in our survey.
All of the demographic variables of the participants were studied according to their respective distributions and frequencies. They were classified for later comparison based on type of patient care provided by the hospitals they were affiliated with. The critical value for significance was P<0.05. The Shapiro-Wilk test was used to confirm the normal distribution of the variables.
The paired t-Test Student for correlation measures was used to compare the difference in the scores on each one of the scales with the total scores for each model used.
The factor structure of the questionnaire was evaluated using an explorative factor analysis, principal component analysis with Varimax rotation. The number of factors for extraction was based on Kaiser’s eigenvalue criterion (eigenvalue ≥1) and evaluation of the scatter plot.[8] The quality of the factor analysis models was assessed using Bartlett’s test of sphericity and the Kaiser-Meyer-Olkin (KMO) test. Bartlett’s test is a measure of the probability that the initial correlation matrix is an identity matrix and should be <0.05. [9] The KMO test measures the degree of multicollinearity and varies between 0 and 1 (should be greater than 0.50–0.60).[10]
Reliability, internal consistency, and reproducibility were also checked. Internal consistency was estimated using Cronbach’s α and item total correlation coefficients. For a questionnaire to be internally consistent, α levels should be above 0.7. [11] The test-retest reliability (repeatability) was evaluated using the Intraclass Correlation Coefficient (ICC). An ICC value above 0.70 is considered acceptable.[12] Specifically, each correlation between items and by models were assessed with correlation matrix.
We also constructed a Bland-Altman Plot by calculating the mean difference between 2 measurements and the standard deviation (SD) of the difference.13 In this graph, 95% of the differences are expected to be less than 2 times SDs.
Potential floor and ceiling effects were measured by calculating the percentage of participants indicating the minimum or maximum possible scores on the questionnaire. Floor and ceiling effects are considered to be present if more than 15% of respondents gave the highest or lowest possible total score (12), which corresponds to a cut off for above 8.5 points or less than 1.5 on each scale.
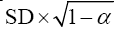
Measurement error is the systematic and random error of a participant’s score that is not attributable to true changes in the construct to be measured.[14] Measurement error is expressed as a standard error of measurement (SEM), which is calculated as:
where SD is the SD of values from all scores,α +is the reliability coefficient.[15]
The percentage of the SEM in relation to the total score of a questionnaire is an important indicator of agreement, and can be interpreted as follows: ≤5% very good; >5% and ≤10% good; >10% and ≤20% doubtful; and >20% negative.[16] Responsiveness was assessed with the Minimal Detectable Change (MDC). The MDC expresses the minimal magnitude of change required to be 95% confident that the observed change between the 2 measures reflects real change and not just measurement error.[17] It is calculated as
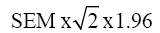
The discriminant validity was assessed by the Pearson correlation coefficient between the items. So we studied the correlation matrix by each model and attribute. A strong correlation was considered to be over 0.60; a moderate correlation between 0.30 and 0.60; and a low (very low) correlation below 0.30.[12]
We could not assess convergent validity of the questionnaire because there are no gold standard or previous studies available for comparison with our results.
The questionnaire for evaluating the models was completed by 27 surgical orthopedists (79.4%), 11 of whom were affiliated with top level hospitals, eight with second level care hospitals, and the eight other doctors to third level care hospitals. Only five residents filled out the questionnaire, and the rest of the surgeons had a mean number of years as practicing specialists of 10.1 (minimum: 0; maximum: 30) years. There was no missing data on the surgeons’ questionnaires; therefore, the number relation of answers per questionnaire was 4.5.
The main results of the six attributes by model is shown in Table 1. Globally, the total score obtained was 35.49 (CI 95%: 32.33-38.64) for Model I and 38.72 (CI 95%: 35.78-41.65) for Model II; normal distribution can´t be rejected in both cases.
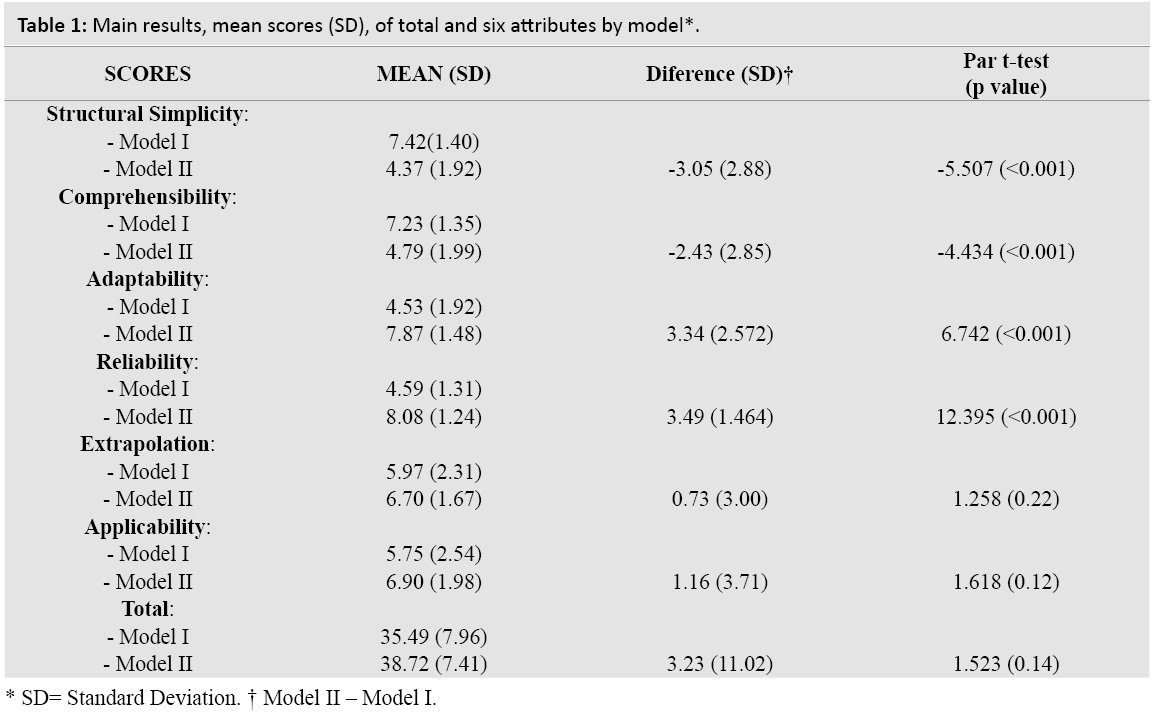
Therefore, the difference found between the two models was not statistically significant at 3.23 points (t=1.523; P=0.14).
Of all the scores obtained, only adaptability for Model II (kurtosis=4.054) showed asymmetrical distribution. When the attributes were evaluated individually, a statistically significant higher score was found for Model I as opposed to Model II for structural simplicity and comprehensibility with a difference of 3.05 (CI 95%: 1.91 to 4.19) and 2.43 (1.31 to 3.56) points respectively. The differences obtained were statistically significantly higher for Model I for adaptability at 3.34 (CI 95%: 2.32 to 4.35) and for reliability at 3.49 (CI 95%: 2.91 to 4.07). However, there were no significant differences in the scores for the rest of the attributes: 0.73 (CI 95%: -0.46 to 1.91) for extrapolation and 1.16 (CI 95%: -0.31 to 2.62) for applicability.
Our results suggest that the main difference between the two pharmacoeconomic models was found in the scoring given by surgeons with less experience (up to 3 years). No analysis comparing specialist surgeons with those doctors still in training was made, since our sample of residents only included five doctors. We did not find differences between scores for the two models when analyzed according to the level of care at the hospitals the surgeons were affiliated with (Figure 1).
Upon analyzing the pattern of answers together with the table of frequencies for the items, no ceiling effect was observed. Interestingly enough, most scales show a ceiling effect in some models, but not in others. Such is the case regarding structural simplicity, comprehensibility, adaptability and reliability. The attributes of extrapolation and applicability show ceiling effects strictly speaking, since they are present in both models. But this effect is moderate, and is found at only a few percentage points above the cut-off point initially set at 15%.
It is the responses regarding adaptability for Model II that show higher scores, although this result is distorted by an anomalous value (surgeon number 20 who gave a score of 3), which, if it were eliminated, would vary between 6 and 10. An analysis of missing values is not necessary since all items were answered. There were ten far removed or important values: 7 for Model 1 (structural simplicity-3, comprehensibility-3, and adaptability-1) and 3 for Model 2 (structural simplicity-1, comprehensibility-1, and adaptability-1).
The SEM was calculated at 0.796, this being 8.0% with respect to the global scale, a good indicator for agreement. The MDC was 2.21, which corresponds to the significance found for each attribute between models.
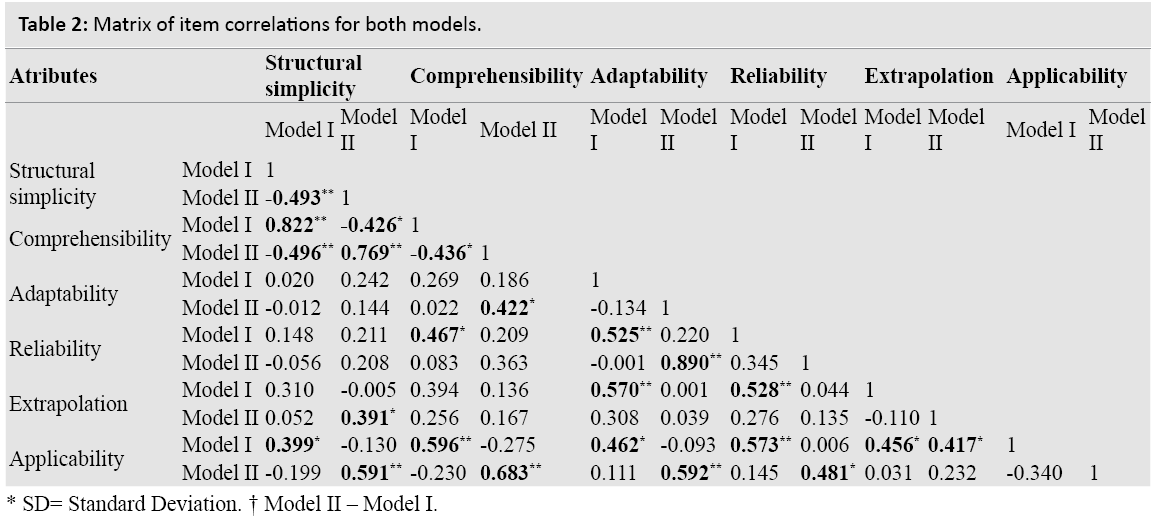
Table 2 shows the Pearson correlations among items, regardless of the model analyzed. Sixty-five point two percent of these were not significant (r<0.4), indicating that there is no correlation between items. Of the other 23 significant correlations, 10 showed moderate correlation (r<0.6) and 13 (19.7% of the total) were very significant. We noted a very strong correlation between comprehensibility and structural simplicity for both models (r=0.822, for Model I and r=0.769 and for Model II). We also noted high correlations between applicability and comprehensibility, which were at r=0.683 for Model II and r=0.596 for Model I. Adaptability showed a higher significant correlation with reliability for Model II (r=890), but nevertheless, was much lower for Model I (r=0.525). The linear relationship between structural simplicity and comprehensibility is demonstrated in the scatter-plot for both models.
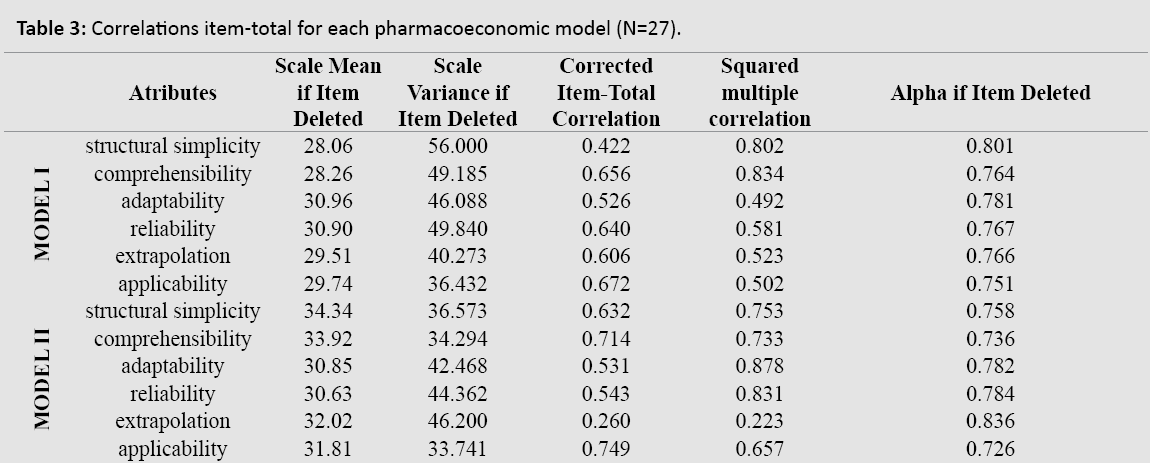
The corrected item-total correlation for the two pharmacoeconomic models is shown in Table 3. The total Cronbach’s alpha was 0.803 for Model I and 0.805 for Model II. The items with less internal consistency were structural simplicity and adaptability for Model I while for Model II they were extrapolation (item-total=0.260) and adaptability. Similar conclusions were found for “squared multiple correlation” or alpha “if item deleted”.
The intraclass coefficient correlation (average values) for evaluation agreement between the two models was 0.609 (CI 95%: 0.385 to 0.785), and the coefficient for evaluation consistency was 0.721 (CI 95%: 0.536 to 0.854) which coincides with Cronbach's alpha (0.721). Both coefficients were statistically significant (F=3.588; P<0.05), showing internal coherence on the measurement range.
The Bland-Altman agreement graph shows the average differences between Model II and Model I with scores for each surgeon who answered the questionnaire (Figure 2), which gives a normal distribution (Shapiro-Wilk test: P=0.859). Lin's concordance correlation coefficient of absolute agreement = -0.002417 (CI 95%: -14.90 a 22.36). Only two surgeons gave scores outside the agreement interval between the two models. One of these doctors is a resident and gave a difference of -23 points. The other doctor who had scores outside the agreement interval of CI 95% is a surgeon with two years’ experience in a top level care hospital. The causes of these two doctors’ scores should be investigated before deciding whether or not to include them in the final decision as to which scale to use.
In the factorial analysis we found a very significant Bartlett's test of sphericity (220.333; p<0.01), indicating that the hypothesis that all the correlations between the variables is null, is quite improbable, and so it would be very interesting to factorize this matrix. The KMO measure of sampling adequacy was 0.525. In the principal analysis of components, the first 4 components explain more than 82.5% of the total variance, and concords with the sedimentation graph obtained, suggesting a final solution of only four components.
When we carry out Varimax rotated factorial analysis for pharmacoeconomic models, we obtain the best result with 2 components for each one. These two factors explain 75.8% and 75.9% of the variance in Model I and Model II respectively. Figure 3 shows the Scatter plot of the principal component analysis for both models with identical solutions, although one intuits from the results for Model II, a 3 factor solution. For Model I, the attributes that carry the most weight for the first factor are adaptability, reliability and extrapolation; and for the second factor, they are structural simplicity and comprehensibility; applicability carries the same explanatory weight for both factors. For Model II, we have the same weights with the exception of extrapolation, which carries more weight for the second factor. Therefore, the two-factor solution for each pharmacoeconomic model is adequate and the attributes studies group themselves together as we had initially expected.
For our phases of investigation we have used two statistical analyses: one designed for a descriptive analysis applied to the results obtained from the questionnaire, and the other for a factorial analysis to check the reliability of our tool by calculating Cronbach’s alpha.[11] We also used two decision trees since they explain acute medical and surgical events such as DC better than others (Markov models). They also have the advantage of maximum design flexibility and greater interpretability for clinics.[18] Our results show no superiority of one pharmacoeconomic model over the other in the total scores obtained from the survey, but there are significant differences in the scores on several scales. We did not find differences in scoring according to the characteristics of the doctors interviewed, including their years’ experience, and the level of health care at the hospitals they are affiliated with. This may be because DC is a very common condition in our part of the world, and surgeons are very familiar with it.
For Model I, the simplest one had the best scores for structural simplicity and comprehensibility. These two attributes showed a clear linear correlation in both models, making it possible to eliminate one of them from the global evaluation of pharmacoeconomic models for treating DC. This high correlation was confirmed in the correlation matrix analysis (Table 3). Model II had the highest scores for adaptability and reliability, apparently because they are better adapted to real clinical conditions. This last conclusion should be confirmed independently with studies involving a larger sample.
Detailed analysis of the distribution of the scores obtained for the specific items, showed no especially anomalous behaviors. Therefore, we can state that the pattern of answers obtained falls within the normal range and so does serve to measure the attributes under consideration. The question is confirmed by the coincidence of the calculated MCD with the average significant differences for each attribute.
The strength of our study, based on the results obtained, is acceptable at 71.0% for a two-side test and 80.8% for a one-side test. We can state that the probability that our results are true is moderately high if we do not know the direction of the expected differences, and high if the direction is known (beta risk <20%). Our data is likely to be useful for sample calculation for future studies to measure clinical validation for pharmacoeconomic models based on our MCD.
The reliability of the scores obtained was good, achieving a Cronbach’s Alfa higher than 0.7, although the authors propose levels greater than 0.8 for discriminatory scales. The Bland- Altman graph, as well as the corrected item-total correlation and the squared multiple correlation obtained confirm these results and demonstrate the validity of the questionnaire used.[13] Both the Bartlett's test of sphericity, and the KMO obtained with the analysis of the principal components suggest a need to carry out a subsequent factorial analysis.10 We obtained a 4-factor rotated Varimax solution, which is close to what we had initially expected. The factorial analysis for differentiated models is very poor since our sample size was small.
In our study, the validity of the pharmacoeconomic models used is guaranteed, firstly, by the scores given by the expert surgeons we interviewed. Validity is also helped along by the oral instructions we gave to the surgeons before they filled out the survey. None of the surgeons expressed any doubt that the models reflected all possible treatments for DC. Another proof of validity is the fact that Model I has actually been used with other published pharmacoeconomic studies on DC.[6,7]
Anytime a person expresses an opinion, he/she is making a subjective judgment which can be evaluated if it is studied adequately. The tools used in studies on quality of life related to health are a good example. Another correct way to gather and analyze these preferences is to use the opinions of experts as in the Delphi method (1, 19), whether modified or not. Published pharmacoeconomic studies do not generally explain whether or not the models used were validated clinically nor do they explain the methodology. Many times, it is up to the analyst, himself, to construct the model.[19]
Surely, we should assure credibility, validity, and precision for pharmacoeconomic models. To this end, international guidelines have been developed for evaluating the methodological quality of pharmacoeconomic studies. CHEERS makes explicit reference to this in point 13b on Model-based Economic Evaluation: describe approaches and data sources used to estimate resource use associated with model health states; describe primary or secondary research methods for evaluating each resource item in terms of unit cost; and describe any adjustments made to approximate opportunity costs.[20] But there is no specific mention of clinical validation of models even though it describes and gives reasons for the specific types of decision-analytical models used (providing a figure to show model structure is strongly recommended) in item number 15. [20]
In our opinion, pharmacoeconomic models need to be clinically validated, considering all possible changes in their structures or in the states of health that should be born in mind. The significance of this is that not just one model exists that truly reflects the reality of an illness and its treatment. And this means that we should seek out the model that best adapts to the clinical necessities of our patients, so that we can make the most appropriate decisions (18). It also requires bearing in mind cultural, idiomatic, and health care system aspects when selecting the best pharmacoeconomic model for each case.
The first limitation of our study results from the small size of the sample (n=27) for a survey. Still, considering that we are talking about experts who are providing opinions on a subject on which they are specialists, our judgment is that our sample size may be sufficient.
The second limitation we highlight is the absence of a reference test for Dupuytren’s contracture that would allow us to objectively measure the validly of the questionnaire used in our study. For this reason, it is not possible to present convergent or discriminant validation data with respect to other questionnaires previously used. Undoubtedly, this fact limits the possibilities for extrapolation of the clinical validation obtained from the present study.
What we present are the results of a not previouslyvalidated survey. It is even possible that the questions included in the questionnaire do not strictly reflect the attributes or the dominions to which we refer conceptually. This is why we used the methodology of questionnaire evaluation to demonstrate the validity and reliability of the scores provided by the experts. To the best of our knowledge, this is the first time such an approach has been used for clinical validation of DC treatments.
The results of our study confirm that it is possible to use a survey to clinically validate a pharmacoeconomic model in a manner that is sure, easy, and inexpensive, compared to other strategies. Undoubtedly, more studies are needed to define which attributes should be measured to clinically evaluate pharmacoeconomic models. We consider this study as a foregoer for a gold standard questionnaire and the correct methodology for evaluating and applying it to the field of pharmacoeconomics.
Clinical validation for pharmacoeconomic models for managing DC with surgical treatment (fasciectomy) or with CCH, has been shown to be feasible, flexible, and economical. The survey used demonstrates acceptable psychomotor properties for clinical validation of pharmacoeconomic models for treating DC.