European Journal of Experimental Biology Open Access

Keywords

GGE biplot; Multi-environment trials; Bayesian approach

Introduction

Multi-environment trials (MET) are used to identify superior crop genotypes for a target environment in plant breeding programs [1,2]. Selecting the best genotypes, with stable and high yield across a number of environments presents statistical issues in the presence of significant genotype x environment interaction (GEI) due to changes in the magnitude of the genotypic response across the environments [3]. GGE biplot has been shown to be very useful for analyzing MET datasets and identifying adaptable genotypes with high yield performance in several studies [4-6]. The GGE biplot analysis exhibits the aspects of genotype stability and adaptability, when a high proportion of the sum of squares of G+GEI could be retained in first two principal components [7]. The polygon view of the biplot is the sound way to visualize the interaction patterns between genotypes and environments [8]. Yan and Kang (2003) have shown the presence or absence of crossover GE interaction which is helpful in identifying different mega environments. Recently, the extensive usefulness of GGE-biplot has been elucidated for analyzing data from multi-environment trials in wheat [9]. These aspects make GGE biplot a most comprehensive tool in plant breeding. GGE biplot is for: 1) carrying out mega-environment analysis (see example, [10-12]: 2) genotypes evaluation (the mean performance and stability) and 3) environments’ evaluation (the power to discriminate among genotypes in target environment). A two-way table of GE data may be analyzed through the joint use of analysis of variance (ANOVA) and singular value decomposition (SVD) in term of principal component analysis (PCA) [13].

In an ongoing crop improvement program, priors information is available for distribution of variance components, for example, for genotypes and genotype x environment integration. These can be used to improve the results on the predication of GE means. The commonly used frequentist approaches also not make use of such information. The analysis of multienvironment trials with a view to estimate genotypes stability can be carried out using a Bayesian approach. Edwards and [14] modeled heterogeneity using exponential of an additive model followed by assigning suitable priors to the variance components of the effects terms of the model. Crossa et al. have studied some practical and theoretical aspect of Bayesian stability in the context of additive main effects and multiplicative interaction (AMMI) and posterior means for genotype × environment interaction component using Gibbs sampler and applied to data on maize [15]. Applications of the Bayesian approach to the AMMI model and GGE have been presented by Josse et al. [16] and da Silva et al. [17]. Using Bayesian analysis, Omer et al. conducted a similar study on genotype × environment interactions and the GGE-biplot assessment of balanced classifications with missing values [18]. Bayesian analysis of GGE biplot models and its implications for the interpretation of the biplots have been discussed in de Oliveira et al. [19]. The purpose of this study is to compare Bayesian and frequentist approaches for GGE biplot of sorghum genotypes yields in six environments in Sudan. The first section presents a frequentist approach, the commonly used GGE biplots. The second section is Bayesian GGE biplot analysis obtained from posterior estimates of genotype × environment interaction of predicted means of grain yield.

Materials and Methods

Experimental data set

Eighteen genotypes of sorghum were evaluated in randomized complete block design (RCBD) during three growing seasons, 2009/10 to 2011/12, at two different locations (North Gedarif and South Gedarif) in Sudan. Data on grain yield in kg/ha was recorded for analysis.

Statistical analysis

Analysis of variance (ANOVA) and REML methods were applied on the combined data using Genstat software [20] to obtain the frequentist estimates of variance components and predicted means while R2WinBUGS was used to obtain posterior means under Bayesian approach. GGE biplot graphs were drawn based on predicted means of under frequentist and Bayesian approach. Therefore, the Bayesian posterior means of GE two ways table based on priors for the SDCs, priors were obtained by using data on sorghum yield (kg ha^-1) from three similar experiments conducted to evaluate 18 genotypes in RCBDs with four replications during 2006/07- 2008/09 at Rahd station in Sudan. A priors information and the WinBUGS and R codes are available [21], the number of iterations was set at one 50,000, the number of chains was set at three, and the last 5,000 simulated values of the parameters were taken for evaluating the posterior distributions.

The Bayesian approach uses prior information which was considered in terms of distributions for variance or standard deviation components for effects of blocks within environments, genotypes, environments and GEI and experimental error variances σ_e², assumed to be homogeneous across environments. The a priori distributions of the variance components in terms of the scale parameters, in the GEI model in the application were taken from past data for half-normal distributions. The prior of half- normal distribution was used for the various standard deviation components of the data model. Using the best a priori distributions, the a posteriori expected values of predicted GE means were obtained (details are aimed for presentation in a separate publication and are not included here). Details of the deviance information criterion (DIC), a Bayesian counterpart of the Akaike information criterion (AIC) for model selection, and selection of the best priors data see [22,23].

The Bi-plots model

Yan and Kang (2003) observed phenotypic variation (P) of genotypes across environments is made up of environment variation (E), genotype variation (G) and genotype-byenvironment (GE) interaction variation Yan [24,25]. This can be written as P-E=G+GE, usually E is the dominant source of variation separate for genotype, so environmental means are removed and analysis concentrates on the genotype variation and genotype-by-environment interaction [26]. The sum of these two terms can be approximated as first two principal components to obtain GGE bi-plot using Genstat software. The basic model for a GGE bi-plot is given as

Y_ij=μ+b_j +α_i+d_ij (1)

Where Y_ij=the estimated yield of genotype i in environment j, μ=the grand mean of all observations, α_i=the main effect of genotype i, b_j=the main effect of environment j and d_ij=the interaction between genotype i and environment j. Instead of trying to separate G and GEI, a GGE biplot model accounts G and GEI together and expresses their joint contribution G+GEI into two multiplicative terms [27]. Thus, the GGE bi-plot model can be rewritten as

Y_ij=μ+ b_j+γ₁P_i1δ_j1+γ₂P_i2δ_j2+ε_ij (2)

where γ₁ and γ₂ are the singular values (SV) for the first and second principal component (PC1 and PC2), respectively, P_i1 and P_i2 are elements of eigenvectors of genotype i for PC1 and PC2, respectively, δ_j1 and δ_j2 are elements of eigen vectors of environment j for PCl and PC2, respectively, ε_ij is the residual associated with genotype i in environment j. PC1 and PC2 eigenvectors cannot be plotted to uniquely construct a meaningful bi-plot before the singular values are partitioned into the genotype and environment eigenvectors. Singular-value partitioning is implemented by,

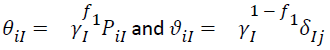(3)

Where, I=1,2 and f1 is the partition factor for PC1. Theoretically, f₁ can be a value between 0 and 1, f₁=1 is most commonly used and is interpreted as environment focused. To generate the GGE bi-plot, the equation [1] is presented as:

Y_ij=μ+ b_j+θ_i1ϑ_1j+θ_i2ϑ_2j+ε_ij (4)

In a bi-plot, genotype i is displayed as a point defined by all θ_iI values (i=1,2) on PC1 (x-axis) and PC2 (y-axis), and environment j is displayed as a point defined by all ϑ_Ij values [28].

Bayesian approach for evaluating genotype and environment interaction

From Bayesian perspective, model in equation (1) can be rewritten as

Y_ij|θ_i,ϑ_i,b_j,α_i,σ_e^2~N(μ+β_j+R_kj+G_i+GE_ij,σ_e²)

The variance components of various effects and interactions in equation (1) will be assumed to be random variables having distributions, called the a the priori distribution, with known parameters. The Bayesian methodology for evaluating genotype and environment interaction (GEI) was presented by Omer at al. on an unbalanced dataset of sorgum yields. In this context, frequentist and Bayesian GEI data model will be used for investigating GGE bi-plot analysis when the dataset is balanced for genotypes and environment classifications.

Results and Discussion

The estimates of variance component, Table 1 indicated that the GEI was significant (P<0.01) under both the approaches. Variation due to G was significant under Bayesian and frequentist approach. Bayesian approach, compared with the frequentist approach, gave the better differentiation of genotypes as assessed in term of variance component and standard error.

Table 1: Summary of the estimates of variance components from combined analysis of grain yield in the evaluation of 18 sorghum genotypes in 6 environments under frequentist and Bayesian approach.

Predicted values of the genotype and environment interaction

The a posteriori means of the GE predicted values is shown in Table 2 (Bayesian approach). Table 3 gives the predicted means of GE under frequentist (REML method). Genotypes are denoted as G1, G2,…, G18 and environment as E1, E2,…,E6. Table 2 shows that G10 was the best genotype in environments E1, E4 and E5 with yields 227.3, 572.5 and 307.3 kg/ha respectively. While G13 was the best genotype in environment E2 (yield=491.8 kg/ha), G18 was best in E3 (yield=1010 kg/ha) and G15 in E6 (yield=1636 kg/ha).

Table 2: Bayesian mean predicted of grain yield (kg/ha) of 18 sorghum genotypes (G1 to G18) across the sex environments E1 to E6 comprising two locations and three years.

Table 3: Frequentist mean predicted of grain yield (kg/ha) of 18 sorghum genotypes (G1 to G18) across the six environments E1 to E6 comprising two locations and three years.

Table 3 shows that the G10 yielded highest in environments E1, E4 and E5 with 259, 622.1 and 356.3 kg/ha, respectively. G13 was the best genotype in environment E2 (yield=574.4 kg/ ha), G18 in environment E3 (yield=951.4 kg/ha) and G15 in environment E6 (yield=1627.5 kg/ha). Genotypes G10, G13, G15 and G18 gave the highest yield under both the approaches in an environment were found best. The posterior means were estimated with a higher precision compared to the frequentist approach (Tables 2 and 3). For instance, average standard error a genotype in environment E1, mean in 38.66 kg/ha under Bayesian approach and 70.03 kg/ha under frequentist approach.

GGE bi-plot analysis

The partitioning of GGE interaction under Bayesian approach (Table 2) in two principal components showed that PC1 and PC2 accounted for 67.80% and 13.84% respectively, and thus explaining a total of 81.64% variation. While for the Frequentist estimates, the corresponding values were 47.29% for (PC1) and 24.62% for (PC2) and 71.84% for total variation. The total percentage variance explained by the two component representation was more effective in Bayesian case compared to frequentist approach. Thus the predicted values of GE means under Bayesian method assemble a clearer pattern between genotypes and environment in smaller number of components, compared to frequentist approach. The bi-plots have been shown by polygon views in Figure 1 (Bayesian approach) and Figure 2 (Frequentist approach). The comparison views of biplots have been shown in Figure 3 (Bayesian approach).

Figure 1: The GGE scatter biplot based on the 18 sorghum genotypes (1,…18) of yield performance trial for 6 environments (E1 to E6). Where, E1=North-Gedarif (2009), E2=South-Gedarif (2009), E3=North-Gedarif (2010), E4=South-Gedarif (2010), E5=North-Gedarif (2011), E6=South-Gedarif (2011). Polygon view of the GGE bi-plot of 18 genotypes based on predicted means under Frequentists (A) and Bayesian (B) approach.

Figure 2: Comparison plots based on the 18 sorghum genotypes (1,…18) of yield performance trial for 6 environments environments (E1 to E6). Where, E1=North-Gedarif (2009), E2=South-Gedarif (2009), E3=North-Gedarif (2010), E4=South-Gedarif (2010), E5=North-Gedarif (2011), E6=South-Gedarif (201). Polygon view of the GGE bi-plot based on of 18 genotypes based on predicted means Frequentists (A) and Bayesian (B) approach.

Figure 3: Ranking plots based on the 18 sorghum genotypes (1,…, 18) of yield performance trial for 6 environments (E1 to E6). Where, E1=North-Gedarif (2009), E2=South-Gedarif (2009), E3=North-Gedarif (2010), E4=South-Gedarif (2010), E5=North-Gedarif (2011), E6=South-Gedarif (2011). Polygon view of the GGE bi-plot based on of 18 genotypes based on predicted means Frequentists (A) and Bayesian (B) approach.

It has been pointed out that PC1 of a GGE bi-plot approximates the genotype main effects (mean performance) and PC2 approximate the GEI effects associated with each genotype, which is a measure of instability. In frequentist, the genotypes with the best response to particular environments to identify specifically adapted genotypes, we grouped G14 and G15 had the highest yielding performance in environments E6, and the G17 and G18 performed well in the environments E4 and E3 whereas G2, G5, G8 and G9 were poor in E1, E2 and E5 environments. For instance, the G15 had the highest yielding performance in environments E6 and G18 well performed in the environments E3, whereas G2, G5, G8 and G9 were poor in E1, E2 and E5 environments with low yield performance.

Comparison GGE bi-plot is used to evaluate the genotypes relative to an ideal genotype. This genotype has large PC1 scores (high mean yield) and small (absolute) PC2 scores (high stability). In Bayesian approach, genotypes G13, G15 and following to G10 and G17 were more desirable than other durum genotypes Polygon view (Figure 1). A genotype is more favorable if it is closer to the ideal genotype position. Therefore, in frequentist approach, genotypes G17 and following to G10, G13, G2 and G15 were more desirable than other genotypes using Polygon view (Figure 2). Using the comparison plot, Bayesian approach highlighted that genotype G15 and following to G14, G17 and G12 were more desirable than the other genotypes. While poor genotypes were G4, G3, G1 and G16 ordinarily (Figure 3). In frequentist approach, genotypes G15 and following to G14, G17 and G12 were more desirable than other genotypes and poor genotypes were G4, G3 and G1, ordinarily (Figure 4). In this way one can compare the two approaches for GGE biplot analysis because it allows visual interpretation of GE interaction. In both approaches, it seems that GGE bi-plot methodology is a proper tool for identifying high yielding genotypes as the most stable ones. Bayesian GGE bi-plots can be used as a new approach for visualizing GGE biplot on the statistical model of principal component analysis (PCA). The difference between the two approaches in GGE biplot analysis is based on differences in the predicted GE means. The Bayesian approach of GGE bi-plot showed higher variability accounted for by the total PCA compared to the frequentist approach. GGE bi-plot analysis way be used for quick visual evaluation and comparison based on the two approaches. These issues are critical because they are inherently related to the validity and scope of the functionalities and capabilities claimed by proponents of GGE bi-plot analysis. The Bayesian codes can be obtained from the first author.

Conclusion

GGE bi-plot methodology, as has been shown to be useful in the analysis of MET dataset, with a view to have a graphical assessment of relationships among genotypes and test environments for a combined response in terms of GEI and genotypic performance (GGEI). The Bayesian approach integrates the prior information available from already conducted trials with that of the current dataset and provides a more realistic and wider coverage for statistical inference. Predicted GE means were obtained using Bayesian and frequentist approaches. Bayesian GGE bi-plot analysis can be easily used to draw conclusions and make right decisions.

Acknowledgments

The authors are grateful to Mr Mohammed Hamz Mohammed, Cereal Research Center, Agricultural Research Corporation (ARC), Wad Medani, Sudan for providing the data used in the illustration. First author is grateful to ICARDA and Arab Fund for Economic and Social Development (AFESD) for granting a fellowship for carrying out the research study.

References

1. Gauch JRHG, Zobel RW (1988) Predictive and postdictive success of statistical analyses of yield trials.Theor Appl Genet 76: 1-10.
2. Delacy IH, Basford KE, Cooper M, Bull JK (1996) Analysis of multi-environment trials an historical perspective. Plant Adaptation and Crop Improvement. Eds. M. Cooper and G. L. Hammer. CAB international, UK.
3. Kaya Y, Akçura W, Taner S (2006) GGE-Biplot Analysis of multi-environmentyield trials in bread wheat.Turk J Agric For 30:325-337.
4. Yan W, Kang MS, Ma B, Woods S, Cornelius PL (2007) GGE Biplot vs. AMMI analysis of genotype-by-environment data. Crop Sci 47: 643-655.
5. Gauch HG (2006) Statistical analysis of yield trials by AMMI and GGE. Crop Sci 46: 1488-1500.
6. DingM, Tier B, Yau W (2007)Application of GGE biplotanalysis to evaluate genotype (G), environment (E) and GxE interaction on P. radiata: A case study. Australasian Forest Genetics Conference Breeding, Tasmania, Australia.
7. VoltasJ, van EeuwijkFA, IgartuaE, del MoralLFG, Molina-Cano JL, et al. (2002)Genotype by Environment Interaction and Adaptation in Barley Breeding: Basic Concepts and Methods of Analysis. Food Product Press, New York.
8. Sabaghnia N, Karimizadeh R,Mohammadi M (2013) GGL biplot analysis of durum wheat (Triticum turgidum spp. durum) yield in multi-environment trials.Bulg J Agric Sci 19:756-765.
9. Yan W, Rajca I (2003) Prediction of cultivar performance based on single versus multiple years in Soybean. Crop Sci 43: 549-555.
10. Farshadfar E, Reza M, Aghaee M, Vaisi Z (2012) GGE biplot analysis of genotype by environment interaction in wheat-barley disomic addition lines. Aust J Crop Sci 6:1074-1079.
11. Yan W, Tinker NA (2005) An integrated system of Biplot analysis for displaying interpreting and exploring genotypes by environment interactions and exploring genotypes by environment interaction. Crop Sci 45:1004-1016.
12. Yan W (2010) Optimum use of Biplots in the analysis of multi−environment variety trial data. Acta Agronomica Sinica 36:1-16.
13. Yang RC, Crossa J, Cornelius PL, Burgueno J (2009) Biplot Analysis of Genotype × Environment Interaction: Proceed with Caution. Crop Sci 49:1564-1576.
14. Edwards JW, Jannink JL (2006) Bayesian modeling of heterogeneous error and genotype × environment interaction variances. Crop Sci 46: 820-833.
15. Crossa J, Perez-Elizalde S, Jarquin D, Cotes JM, Viele K, et al. (2011) Bayesian estimation of the additive main effects and multiplicative interaction model.Crop Sci 51:1458–1469.
16. Josse J, van Eeuwijk FA, Piepho HP, Denis JB (2014) Another look at Bayesian analysis of AMMI models for genotype-environment data. J Agric Biol Environ Stat 19: 240-257.
17. da Silva CP, de Oliveira LA, Nuvunga JJ, Pamplona AKA (2015) A Bayesian shrinkage approach for AMMI models. PLoS One 10:1-27.
18. Omer SO, Slafab EH, Rathor A (2015) Bayesian analysis for genotype x environment interactions and the GGE-biplot assessment: evaluation of balanced classifications with missing values.Int J Appl Sci Biotechnol 3: 210-217.
19. de OliveiraLA, da Silva CP,NuvungaJJ,da Silva AQ, Balestre M (2016)Bayesian GGE biplot models applied to maize multi-environments trials. Genet Mol Res 15:1-12.
20. Payne RW, Harding SA, Murray DA, Soutar DM, Baird DB, et al. (2011) The Guide to GenStat Release 14, Part 2: Statistics. VSN International, Hemel Hempstead, UK.
21. Omer SO, Abdalla AWH, Mohammed MH, Singh M (2015) Bayesian estimation of genotype-by-environment interaction in sorghum variety trials. Communications in Biometry and Crop Science 10:82–95.
22. Gelman A, Chew GL, Shnaidman M (2004) Bayesian analysis of serial dilution assays. Biometrics 60:407-417.
23. Gelman A (2006) Prior distributions for variance parameters in hierarchical models. Bayesian Analysis 3:515-533
24. Yan W, Cornelius PL, CrossaJ, HuntLA(2001) Two types of GGE Biplots for analyzing multi-environment trial data. Crop Sci 41: 656-663.
25. Yan W, Kang MS (2003) GGE biplot analysis: a graphical tool for breeders, geneticists and agronomists. Crop Sci47: 641-653.
26. Glaser A (2010) The use of biplots in statistical analysis: with examples in GenStat EuropeanGenStatand ASReml Applied Statistics Conference, VSN International, Hemel Hempstead, UK.
27. Yan W, Glover KD, Kang, MS (2010) Statistical test of genotype-by-environment interaction patterns observed from a Biplot. Crop Sci 50:1121-1123.
28. FarshadfarE,RashidiM,JowkarMM,Zali H (2013) GGE Biplot analysis ofgenotype × environment interaction in chickpea Genotypes.Eur J Exp Biol 3:417-423.