Archives in Chemical Research Open Access

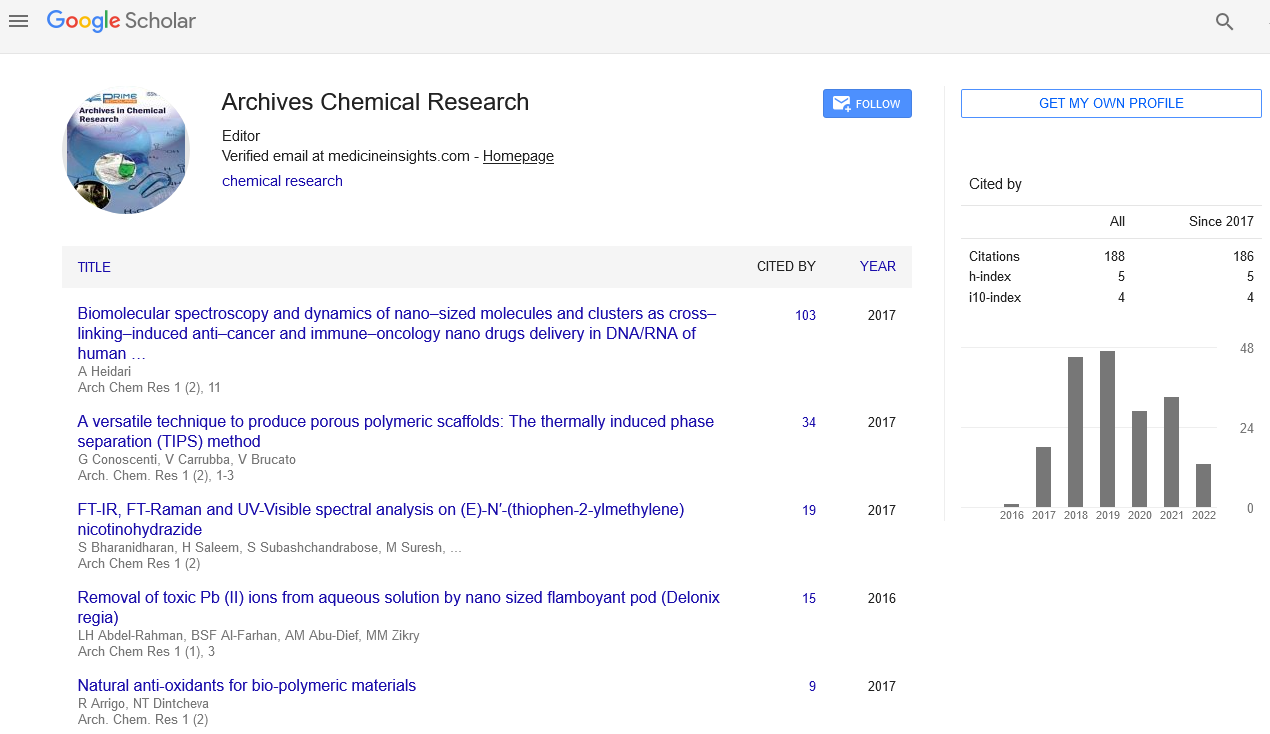
Keywords

Silver; Electrical modulus; Polymer; Electrolyte

Introduction

One of the intriguing classes of solid state coordination compounds is a polymer electrolyte that utilizes solid but flexible membranes for ionic conductivity [1]. Because of the attractive interaction between cations and chains, chains polymers can function as solvents for certain salts if they have electro-negative atom (nitrogen or oxygen) within their repeat unit [2]. Chitosan polymer contains both atoms, as shown in previous studies [3]. Electro chromic displays, sensors, fuel cells and batteries are some of the applications of polymer electrolytes [4,5]. The mechanism for their conductivity is still not understood fully, despite the many studies [6]. The amorphous phase is the main conductivity phase, despite both crystalline and amorphous phases coexisting [7]. Little is understood about the coupling between ion transport and polymer segmental relaxation in polymer electrolytes, and could be the key for new discoveries [8].

Within the polymer electrolytes, both dipoles and charge species affect the relaxation dynamic and frequency dependent conductivity, as has been reported [9]. Electric modulus formalism M" can be used as an environment for studying relaxation dynamics, specifically dielectric relaxation [10]. M" displays a pronounced peak, leading to modulus representation and associating the extend of conductivity with time scale τ.

Despite the well establishment of relations between the various quantities, yet there is still debate on modulus representation [11]. When the electric displacement is constant, from physical view point, the relaxation of electric fields in material is correspondent to electrical modulus [12]. Emphasizing small features at high frequencies and suppressing the high signal intensity associated with electrode polarization is the main benefit of modulus representation [11]. Therefore, studying relaxation times and conductivity in polymers and ionic conductors can be achieved through electric modulus spectra [13].

In the thin film preparation of chitosan-silver triflat polymer electrolyte for this paper, chitosan has been used as a base polymer. Amine and hydroxyl functional groups make up a chitosan polymer, and they are suitable for solid polymer electrolyte preparation since they have lone pair electrons [14].

Silver salts like AgSbF₆, AgCF₃SO₃, AgBF₄ and AgClO₄ are dissolved into polymer hosts like and poly (vinylpyrrolidone) (PVP), poly(ethylene oxide) (PEO) and poly(2-ethyl-2-oxazoline)(POZ) to make silver-based polymer electrolytes, and this is the result of coordination interaction between silver ions and polar groups [15,16]. Olefin transport is facilitated essentially by nitrogen and oxygen atoms contained within polar polymers, and production of silver metal particles by reducing silver ions is another function of theirs [17], due to the capability of nitrogen and oxygen atom's lone pair electrons to easily reduce silver ions [18]. These lone pair electrons of oxygen and nitrogen atoms are also used for occurring complexation in addition to reduction of silver ions.

Due to these properties, the effect of silver nanoparticle reduction from silver ions on the properties of electrical modulus of chitosan-silver triflate solid electrolyte is studied in this paper over a wide range of temperature and frequency.

Experimental

SPE thin film preparation

Silver triflate (AgCF3SO3) with a molecular weight 256.94 (supplied by Fluka, ≥99 purity, Germany, CAS No. 2923-28-6) and Chitosan from crab shells (≥75% de acetylated, Sigma Aldrich, USA, CAS No. 9012-76-4) were used in this study as raw materials. Solution cast technique with the solvent being acetic acid (1%) is used for the preparation of solid polymer electrolyte (SPE) films. 1g of chitosan is dissolved in acetic acid solution and fixed in the current system. Varying amount of silver triflate (AgCF3SO3) ranging from 2 to 10 wt% in steps of 2 wt% is added to this system to make different compositions of chitosan-silver triflate electrolyte in weight percent ratios; 98:2, 96:4, 94:6, 92:8 and 90:10 for chitosan: AgCF3SO3 and 100:0 for pure chitosan acetate. To obtain homogenous solution, the mixture is continuously stirred until said result is obtained. In room temperature, the solutions are left to dry in different Petri dishes after casting, in order to form the films, then further drying is done by transferring into desiccators. The result is a solvent free and mechanically stable film.

Complex Impedance measurement

Characterization of the material's electrical properties is done through the complex impedance spectroscopy. Small discs of 2 cm diameter are made from the SPE films, and to ensure proper electrical contact between the sample and electrodes, two clean stainless steel and circular in shape electrodes are used under spring pressure. This helps with the problem of air interstices in between the electrodes and sample interface. HIOKI 3531 Z Hi-tester (made in Japan, No.1036555) is used to measure the impedance of films, as it was interfaced in the frequency range from 50 Hz to 1000 KHz to a computer. The imaginary and real parts of the impedance is calculated and measured by the software. The real (M′) and imaginary (M″) parts of complex electric modulus (M*) is evaluated by the use of the real (Z′) and imaginary (Z″) part of complex impedance (Z*) [19].

A is the area of the film, where it is the thickness and C0 is the vacuum capacitance and given by ε0A/t. the angular frequency is represented by ω, and is equal to ω = 2πf, the applied field's frequency is f.

UV-vis and TEM characterization

The absorbance mode of Jasco V-570 UV-Vis-NIR spectrophotometer (Japan, Jasco SLM-468) is used to record the chitosan-silver triflate electrolyte film's UV-vis spectra. LEO LIBRA (Germany, 120 EFTEM, accelerating voltage 120 kV) instrument was used to record the electrolyte's Transmission electron microscopy (TEM) images. Using a filter paper, excess solution is removed from the dried chitosan-silver triflate electrolyte solution that was placed on a carbon coated copper grid at room temperature.

Results and discussions

Concentration dependence of M″ spectra

M” spectra's frequency dependence at a fixed temperature for different salts. Higher frequency is seen in highest conducting sample of maximum M" peak spectra in comparison to other compositions. Possibly due to polar group relaxations especially at low frequency, pure chitosan and chitosan-silver triflate (98:2) may show more than one peak. Yet in higher salt concentration samples, because of the motion and high free charge carrier concentration within the material, these peaks disappear. Consequently the low frequency relaxation can be hidden due to a high DC conductivity that is produced (Figure 1).

A non-Debye type relaxation is suggested by the broadening of the peaks, which in turn represent the conductivity relaxation peak for the distribution of relaxation times of the free charges [20]. As conductivity increases, the relaxation times decrease, shifting to a higher frequency [21]. Through the relation 2πfmax = 1/τσ, we can calculate the conductivity relaxation times, were f max is a frequency corresponding to M″max and τσ is the conductivity relaxation time. Shows silver triflate concentration function as a variation of τσ. As the salt concentration increases up to 4 wt. % AgCF₃SO₃, the conductivity relaxation ties decrease. We can deduct from the results, especially from four to eight weight percentage of salt there is a competition between ion association and dissociation. Charge carriers concentration increase from 8 wt. % AgCF₃SO₃ to 10 wt. % AgCF₃SO₃ explains the significant drop in conductivity relaxation times, i.e. as the number of mobile charge carriers’ increase; there will be increased conductivity (Figure 2).

M′ and M″ frequency dependence at selected temperatures

At varied temperatures, the imaginary and real part's frequency dependence of the complex modulus for the sample with the highest conductivity (90; 10). Equations were used to calculate the imaginary and real parts of the complex modulus (Figure 3 and 4).

Utilizing the representation of electrical modulus (M*), the conductivity behavior in regards to conductivity relaxation time can be interpreted more conveniently. Ionic conductivity analysis is commonly done by representation of M* through ionic process association with conductivity relaxation time [22]. M′ are very small at lower frequencies as illustrated by electrode polarization is removed the closer the value is to zero [23, 24]. While at higher frequency, M′ increases until reaching maximum value M∞, possibly because of the wide range of relaxation process frequency [25]. The spread of conductivity relaxation over a range of frequencies explains the observed dispersion and pointing to the occurrence of relaxation time and the presence of a loss peak at the same time in the imaginary part diagram of electric modulus versus frequency. ε′ In complex permittivity (ε*) is equivalent to M′ in complex electric modulus (M*) and this explains peak absence in M′ diagram i.e. the materials capability for energy storage is represented by M′. The charge carriers and mobility of the polymer increase with increased temperature is why M′ values decrease. At high temperatures, molecular dipoles and charge carrier's orientation becomes easier.

Clearly shows loss peaks formation. It is possible that the electrode polarization effect with its large value of capacitance causes M″ to exhibit low values in low frequencies [26]; a large amount accumulation of charge carriers at the interface of electrode/solid polymer electrolyte. Yet obvious peaks can be seen at high frequencies. The non-Debye behavior is illustrated by the asymmetric and board peaks on both maxima sides. The region on the right of the peak are carriers that are mobile on short distances and are confined to potential walls, while the region to the left of the peak are carriers that are mobile over a long distance [24]. Experimental frequency limitation explains why at higher temperatures M″ peak spectra disappear (Figure 4).

At high temperatures the formation of silver nanoparticles from reduction of silver ions contributes to the rise of both M′ and M″ above 358K. The function of temperature at a fixed frequency can be used to study M′ and M″ as door way for studying silver ion reduction to silver nanoparticles.

The ion's best conductivity relaxation time τσ is relaxation frequency, which is the frequency associated with the peaks. Demonstrates the variation of reciprocal temperature of log (fmax). In regards to the activation energy, the figure copes with Arrhenius behavior, Ea = 1.16 eV.

The rise in mobility of ionic carriers during rise of temperatures causes a reduction in relaxation time. Almost a straight line is formed by the points, since the regression value R2 is 0.996 meaning (Figure 5).

Argand plots analysis

In the presence of polymer electrolyte the nature of relaxation process can be studied by Argand plot demonstration at different temperatures. The dependence of Argand plot on temperature.

It can be concluded that Debye model (single relaxation time) fails to explain the half semicircle curves of Argand. In this situation especially in polymers to understand the experimental data, a distribution of relaxation time becomes mandatory. Among the many reasons for this distribution is space charge polarization, hopping, and ellipsoidal shape of polar groups and in Homogenetics presence being the most prominent [27]. At lower temperatures, the Argand plot shows deformed arcs with centers localized to below the horizontal axis. The electric relaxation of materials corresponds with this position of the centers as well as distribution and inters correlation of activation energy and relaxation time [28]. There is a shift to toward the origin in Argand curves when temperature rises, as demonstrated. This can be explained by the increase of ionic mobility by the increased conductivity resulting from risen temperature and both Z′ and Z ″ increase subsequently. At 363K the resistance within the sample increases, since a large amount of silver nanoparticles form from silver ions reductions, causing M″–M′ curves to increase (Figure 6).

The dependence of M′and M″ on temperature at selected frequencies

M′ and M″ are temperature dependent at selected frequency. Until 358K due to a rise of ionic conductivity, M′ and M″ decrease as temperature rises because of the dominance of silver ions. However when above 358k, a large of amount of silver ions transform into silver nanoparticles causing M′ and M″ to increase with rising temperature. The ionic motion is hindered by the increase of resistance within the sample caused by increased silver nanoparticles.

The presence and temperature dependence of silver nanoparticles can be detected within the sample by the complex impedance plots. Phase transitions, interfacial effects in polymers and complex systems, molecular mobility and conductivity mechanisms can be efficiently studied by electrochemical impedance spectroscopy [29] (Figure 7a and 7b).

The complex impedance plots at different temperatures shown explain the increase of M′ and M″. The electrode surface polarization phenomena (i.e. tilted spike) is often separated from the bulk material (i.e. depressed semicircle) by the complex impedance plots (Z″ vs. Z′) [30].

The free charges that build up in the interface between the plane geometry's electrode surfaces and the electrolyte form an electric double layer (EDL) capacitance that in turn results in the formation of electrode polarization phenomena (tilted spike) [30,22]. In the current system, the silver nanoparticles act as grain boundaries causing second semicircles to appear at different temperatures (Figure 8).

It is concluded then, that within the same system, silver nanoparticles and silver ions are in a continuous competition. As the temperature rises from 303 to 358k, the bulk resistance decreases, i.e. silver ions are dominant and the system is like an ionic conductor. However once the temperature passes 358k, the bulk resistance increases since more silver nanoparticles are formed from silver ions. Subsequently both M′ and M″ increase since conduction mechanism and overall polarization decrease because of the decrease of silver ions. Z′ and Z″ increase above 358K and the mentioned behavior can be seen from equation. An increase in both M′ and M″ can be seen as well. At this point a no composite behavior is seen from the polymer electrolyte rather than ionic behavior. On the other hand, in regards to pure chitosan the second semicircles are not seen (Figure 9).

More detailed studying of the absorption of UV-vis of chitosansilver triflate (90:10) solid electrolyte and pure chitosan allows for a better understanding of silver ion transformation to silver nanoparticle.

The complex impedance plot for pure chitosan is shown in figure 9 at different temperatures. One observation is that the bulk resistance of chitosan-silver triflate (90:10) solid electrolyte is lower than that of pure chitosan. Also there is continuous decrease in pure chitosan's bulk resistance as the temperature increases up to 393K, differing from chitosan-silver triflate (90:10) solid electrolyte's Z″–Z′ plot. Another observation would be that pure chitosan in its Z″–Z′ plot does not manifest second semicircles as temperature changes.

The common characterization method for studying silver nanoparticle formation and its temperature properties was UV-vis spectroscopy, because a specific UV-vis absorption band is seen for silver nanoparticles and their clusters in ultravioletvisible region [31]. The absorption spectra of UV-vis at ambient temperature (303K) for both chitosan-silver triflate (90:10) solid electrolyte and pure chitosan are shown in (Figure 10).

Chitosan-silver triflate (90:10) solid electrolyte has a broad absorption peak from 400 to 500nm with maximum being at 426nm as demonstrated in the figure, mainly due to the surface plasmon band of silver nanoparticles, on the other hand pure chitosan has no specific absorption peak within the same range. The silver nanoparticle formation is responsible for absorption peak formation especially if maximum is between 420 to 520nm, while the concentration of the silver nanoparticles corresponds with the height of the peak [32, 33].

The absorption spectra of UV-vis at different temperatures for chitosan-silver triflate (90:10) solid electrolyte is shown in figure 11. As the temperature increases from 303K to 393K, the peak heights increase as well from 0.61 to 1.2, giving the understanding that at high temperatures a more rapid conversion of silver ions to silver nanoparticles occurs [34]. Studies report that silver ion reduction occurs by hydroxyl, carboxyl and imide group containing polymers [35, 36], because N and O atoms exhibit strong affinity for metallic silver and silver ions [36] (Figure 11).

Solid membrane's color change from yellow to dark brown is another indicator for silver nanoparticle formation in our system. Similar behavior for PVP-silver salt electrolyte is also mentioned by Kang et al. [37]. Interacting electromagnetic field causes the free conduction electrons to oscillate, collectively it is called Surface Plasmon Resonance (SPR) and it is responsible for the intense original color of chitosan-silver triflate [38].

The surrounding medium's dielectric constant with the nanoparticle's shape and size give the metal nanoparticles its color. However the intense color in the visible spectrum is only seen in electrodes with Plasmon resonance since they have free electrons [39].

In our system, silver nanoparticle observation was done by Transmission electron microscopy (TEM). The silver nanoparticles within chitosan-AgCF3SO3 (90:10) solid electrolyte is shown through a TEM image in figure 12. It shows that they are agglomerated and dispersed. When the repulsion energy is lower than the attraction energy between the particles, it leads to particle agglomeration generally [40] (Figure 12).

Therefore, UV-vis analysis combined with impedance make a valuable support that at higher temperatures both M′ and M″ values increase. As far as we know, change in properties of solid polymer electrolytes (SPE) by the effect of silver ion reduction to silver nanoparticles is reported for the first time.

Scaling behavior of M"

More information can be obtained on the effect of charge carrier concentration, structure and temperature on relaxation dynamics by studying scaling of electric modulus [41]. Figure 13 shows the electric modulus of chitosan-silver triflate (90:10) as its imaginary part is scaled at different temperatures. The parameters of M″ and f are scaled according to M″max and fmax respectively.

A single master curve is formed by merging of all the modulus spectra, meaning for a particular composition the dynamical relaxation is independent on temperature [42]. Deviation from Debye behavior is seen by the dielectric relaxation process evidenced by the asymmetric plot shape and that the distribution of relaxation times is not symmetric [43]. A clear non symmetric plot is seen for the normalized modulus in figure 13, in accordance with electrical function's non exponential behavior, clearly mentioned by exponential function of kohlrausch-William-Watts [44].

Deviation from Debye relaxation is shown as exponent β. The ideal Debye behavior is 1.14 decades, yet in our system the chitosan: AgCF₃SO (90:10) full width half height (FWHH) is nearly 2 decades.

A highly non-exponential conductivity relaxation is concluded from the small value (0.57) of β [42]. Deviation from Debye type relaxation becomes larger the lower the value of β becomes, the standard is (β=1). Clearly a practical solid electrolyte has a less than 1 β value [20] (Figure 13).

Conclusions

The technique of solution casting was not used for preparation of Chitosan-silver triflate electrolytes. The highest conductivity samples have not a shift to higher frequency for their M″ spectra since they have a low number of mobile charge carriers. The systems capacitive nature is demonstrated by M′ long tail in the low frequency range. Non Debye relaxation type is seen in M″ spectra's broad peaks. Relaxation times distribution gives the Argand plots a deformed arc shape. The large amount of iron nanoparticles formed from silver ions at higher temperatures causes the M′ and M″ to increase. The presence and growth of silver nanoparticles is proved by the appearance and temperature dependence of second semicircles in complex impedance plots. The weak affinity between silver ions and hydroxyl and amine groups of chitosan cause a decrease in silver nanoparticles as temperature increases, as shown by the UV-vis spectra. Transmission electron microscopy (TEM) is used for validating the formation of silver nanoparticles. For a particular compositions, a temperature independent nature is seen for the dynamical relaxation processes, as demonstrated by the spectra's scaling behavior. A highly non exponential nature of the conductivity relaxation is concluded from the value of β exponent.

References

1. Karan NK, Pradhan DK, Thomas R, Natesan B, Katiyar RS, (2008) Solid polymer  lectrolytes based on polyethylene oxide and lithium trifluoro- methane sulfonate (PEO-LiCF3SO3): Ionic conductivity and dielectric relaxation. J Solid State Ion 179: 689-696.
2. Dieterich W, Dürr O, Pendzig P, Bunde A, Nitzan A, (1999) Percolation concepts in solid state Ionics. Physical A: Statistical and Theoretical Physics 266: 229-237.
3. Yahya MZA, Arof AK, (2002) Studies on lithium acetate doped chitosan conducting polymer system. J Eur poly  38:1191-1197.
4. Bhargav PB, Mohan VM, Sharma AK, Rao VVRN, (2009) Investigations on electrical properties of (PVA:NaF) polymer electrolytes for electrochemical cell applications. J Curr Appl Phys 9:165-171.
5. Baskaran R, Selvasekarapandian S, Kuata N, Kawamura J, Hattori T (2006) Ac impedance, DSC and FT-IR investigations on (x) PVAc-(1–x) PVdF blends with LiClO4. J Mater Chem Phys 98: 55-61.
6. De Jonge JJ, Van Zon A, De Leeuw SW, (2002) Molecular dynamics study of the influence of the polarizability in PEOx-NaI polymer electrolyte systems. J Solid State Ion 147: 349-359.
7. Avellaned COA, Vieira DF, Al-Kahlout A, Leite ER, Pawlicka A, et al. (2007) Solid-state electrochromic devices with Nb2O5: Mo thin film and gelatin- based electrolyte. J Electrochim Acta 53:1648-1654.
8. Natesan B, Karan NK, Katiyar RS, (2006) Ion relaxation dynamics and nearly constant loss behavior in polymer electrolyte. J Phys Rev E 48 1-4.
9. Singh KP and Gupta PN (1998) Study of dielectric relaxation in polymer electrolytes. J Eur poly 34: 1023-1029.
10. Chabchoub N and Khemakhem H, (2004) Ac ionic conductivity investigations on the CsK (SO4)·Te (OH)6 material. J Alloys Compd 370: 8-17.
11. Richert R, (2002) The modulus of dielectric and conductive materials and its modification by high electric fields. J Non Cryst Solids 305: 29-39.
12. Molak A, Paluch M, Pawlus S, Klimontko J, Ujma Z, et al. (2005) Electric modulus approach to the analysis of electric relaxation in highly conducting (Na0.75Bi0.25)(Mn0.25Nb0.75)O3 ceramics. J Phys D Appl Phys 38: 1450-146.
13. Migahed MD, Ishra M, Fahmy T, Barakat A, (2004) Electric modulus and AC conductivity studies in conducting PPy composite films at low temperature. J Phys Chem Solids 65:1121-1125.
14. Majid SR and Arof AK, (2007) Electrical behavior of protonconducting chitosan-phosphoric acid-based electrolytes. J Phys B: Condens Matter 390: 209-215.
15. Kim JH, Min BR, Wong J, Kang YS, (2003) Anomalous temperature dependence of facilitated propylene transport in silver polymer electrolyte membranes. J Membr Sci 227: 197-206.
16. Kang SW, Kim JH, Won J, Char K, Kang YS, (2004) Effect of amino acids in polymer/silver salt complex membranes on facilitated olefin transport. J Membr Sci 248: 201-206.
17. Kim JH, Wong J, Kang YS, (2004) Olefin-induced dissolution of silver salts physically dispersed in inert polymers and their application to olefin/paraffin separation. J Membr Sci 241:403-407.
18. Lim PY, Liu RS, She PL, Hung CF, Shih HC, (2006) Synthesis of Ag nanospheres particles in ethylene glycol by electrochemical-assisted polyol process. J Chem Phys Lett 420: 304-308.
19. Padmasree KP and Kanchan DK, (2005) Modulus studies of CdI2–Ag2O–V2O5–B2O3 system. Mater. Sci. Eng. B 122: 24-28.
20. Ram M and Chakrabarti S, (2008) Dielectric and modulus studies on LiFe1/2Co1/2VO4. J. Alloys Compd 462: 214-219.
21. Yahya MZA and Arof AK, (2004) Conductivity and X-ray photoelectron studies on lithium acetate doped chitosan films. J Carbohydr Polym 55: 95-100.
22. Pradhan DK, Choudhary RNP, Samantaray BK, (2008) Studies of structural, thermal and electrical behavior of polymer nanocomposite electrolytes. Express Polym Lett 2:630-638.
23. Yakuphanoglu F, (2007) Electrical conductivity and electrical modulus properties of α, ω –dihexylsexithiophene Organic semiconductor.  J Physica B 393:139-142.
24. Dutta A, Sinha TP, Jena P, Adak S, (2008) Ac conductivity and dielectric relaxation in ionically conducting Soda-lime-silicate glasses. J Non Cryst Solids 354: 3952-3957.
25. Patro LN and Hariharan K, (2009) AC conductivity and scaling studies of polycrystalline SnF2. J Mater Chem Phys 116: 81-87.
26. Patro LN and Hariharan K, (2009) Frequency dependent conduction characteristics of mechanochemically synthesized Na Sn2 F5. Mater Sci Eng C: B 162:173-178.
27. Kwan KC, (2004) Dielectric phenomena in solids. Elsevier sci New York, USA.
28. Calleja RD, Matveeva ES, Parkhutik VP, (1995) Electric relaxation in chemically synthesized polyaniline: Study using electric modulus formalism. J Non Cryst Solids 180: 260-265.
29. Calleja RD, Matveeva ES, Parkhutik VP, (1995) Electric relaxation in chemically synthesized polyaniline: Study using electric modulus formalism. J Non Cryst Solids 180: 260-265.
30. Psarras GC, Gatos KG, Karahaliou PK, Georga SN, Krontiras CA, et al. (2007)  Relaxation phenomena in rubber/layered silicate nanocomposites. Express Polym Lett 1:837-845.
31. Sengwa RJ, Choudhary S, Sankhla S, (2008) Low frequency dielectric relaxation processes and ionic conductivity of montmorillonite clay nanoparticles colloidal suspension in poly (vinyl pyrrolidone)-ethylene glycol blends. Express Polym Lett 2: 800-809.
32. Lu J, Suarez JJB, Takahashi A, Haruta M , Oyama ST, (2005) In situ UV-vis studies of the effect of particle size on the peroxidation of ethylene and propylene on supported silver catalysts with molecular oxygen. J Catal 232: 285-295.
33. Kim JH, Kim CK, Won J, Kang YS, (2005) Role of anions for the reduction behavior of silver ions in Polymer/silver salt complex membranes. J Membr Sci 250: 207-214.
34. Liu Y, Chen S, Zhong L, Wu G, (2009) Preparation of high-stable silver nanoparticle dispersion by using Sodium alginate as a stabilizer under gamma radiation. J Radiat Phys Chem 78: 251-255.
35. Kim JH, Min BR, Kim HS, Won J, Kang YS, (2003) Facilitated transport of ethylene across polymer membranes containing silver salt: Effect of HBF4 on the photo reduction of silver ions. J Membr Sci 212: 283-288.
36. Sharma VK, Yngard RA, Lin Y, (2009) Silver nanoparticles: Green synthesis and their antimicrobial activities. Adv Colloid Interface Sci 145: 83-96.
37. Silvert PY, Herrera Urbina R, Duvauchelle N, Vijayakrishnan V, Elhsissen KT, (1997)  Preparation of
38. Colloidal silver dispersions by the polyol process. Part 1 – Synthesis and characterization. J Mater Chem 7:293-299.
39. Kang SW, Kim JH, Oh K, Won SJ, Char K, et al. (2004) Highly stabilized silver polymer electrolytes and their application to facilitated olefin transport membranes. J Membr Sci 236:163-169.
40. Srivastava S, Haridas M, Basu JK, (2008) Optical properties of polymer non composites. Bull Mater Sci 31:213-217.