Research Article - (2015) Volume 1, Issue 1
Yakun Zhu* and Michael L FreeM
Metallurgical Engineering, University of Utah, USA
*Corresponding Author:
Yakun Zhu
Metallurgical Engineering
University of Utah, USA
E-mail: yakun.zhu@utah.edu
Received Date: September 16, 2015; Accepted Date: September 25, 2015; Published Date: November 11, 2015
Citation: Zhu Y, FreeM ML. Effects of Surfactant Aggregation and Adsorption on Steel Corrosion Inhibition in Salt Solution. Polym Sci. 2015, 1:1.
The corrosion inhibition efficiency of mixtures of three homologous benzalkonium chlorides (BAC) surfactants was investigated using electrochemical measurements and modeling. The surface aggregation concentration (sac) and critical micelle concentration (cmc) of surfactant are useful to evaluate inhibition efficiency. A new cmc prediction model for ternary mixed homologous surfactants of interest has been developed. The model is applicable over a wide concentration range of dissolved salt in solution. The combination of the modified Langmuir adsorption model and the cmc prediction model provides a potential method for inhibition efficiency prediction of various mixed homologous surfactant systems at various dissolved salt concentrations.
Keywords
Inhibition efficiency; Surfactant mixtures; Sac; Cmc; Impedance; Model
Introduction
The oil and gas industry, as an important component of the national economy, has received considerable attention from researchers. Unfortunately, oil, mining, and transportation equipment have become increasingly difficult to operate because of equipment damage caused by corrosive media, such as CO2, Cl-, and H2s [1,2]. The annual direct cost of corrosion in the US has been estimated to be approximately $276 billion or 3.1% of the gross domestic product (GDP) while corrosion costs between 1.5% and 5.2% of the GDPs in other countries [3]. About 3.7% out of the total cost comes from the oil and gas infrastructure, which is mainly caused by the corrosion of carbon steel, which is widely used for pipelines. Carbon steel is easily corroded in environments that contain water and carbon dioxide (CO2). Dissolved C02 [4] in water and crude oil can cause tremendous damage to pipelines and structural components [5-7]. These problems have led to great interest in industry and academia to control CO2-related corrosion. The most popular control method is to use organic inhibitors, many of which are surfactants with hydrophilic and hydrophobic molecular sections [8-10]. Upon addition to a pipe (steel)-water-oil environment, surfactants can be involved in adsorption, partitioning, and aggregation [11]. The hydrophilic group of surfactant strongly prefers interaction with polar entities such as water, metals, and other ions. Generally these organic compounds adsorb on the steel surface, block the active sites exposed to corrosive media, and thereby reduce corrosion attack [12,13]. It is believed that the molecular structure of these heterocyclic compounds plays a dominant role in the corrosion inhibition performance. The presence and structure of specific atoms, such as C, H, N and O, in these compounds determines the adsorption mechanism and corrosion inhibition efficiency [14,15]. In practical applications surfactant mixtures have received wide attention due to their superior physicochemical properties and capabilities in efficient solubilization, dispersion, suspension, and transportation [16,17]. Solutions of mixed surfactants can often be conveniently tuned to achieve desired properties by adjusting the mixture composition. More surface-active and expensive surfactants are often mixed with less surface-active and less expensive surfactants to reduce cost [18]. Natural mixtures of surfactants are also commonly used to avoid costly separations. However, the authors are not aware of a completely established theory or model to adequately predict the corrosion inhibition on carbon steel of various mixed surfactants despite extensive research work. The hydrophobic portion strongly prefers interaction with hydrophobic entities such as hydrocarbon phases. When an aqueous surfactant solution comes into contact with an immiscible organic liquid, surfactant monomers may prefer partitioning into organic liquid until equilibrium is reached between the two liquids. Partitioning is usually characterized by the partitioning coefficient, which is defined as the ratio of monomeric surfactant concentration in oil to that in water [19]. For mixed surfactants, the phenomenon becomes more complicated in terms of equilibrium mixture composition in each phase, the effect of individual mixed species on the partitioning, and the adsorption of mixture at the oil/water interface. It has been shown that for some nonionic pure surfactants, a plateau aqueous concentration of monomer beyond the critical micelle concentration (cmc) is reached with increasing total surfactant concentration [20]. However, the total amount of surfactant partitioned into oil phase continues to increase beyond the mixed cmc [20-22], which makes the experimental investigation and quantitative modeling of mixed surfactant partitioning more complicated. In other words, surfactant molecules tend to adsorb at the airliquid interface, liquid-solid interface, or liquid-liquid interface to escape from water by associating and aggregating hydrocarbon chains together. The concentration at which a monomer layer of surfactant forms at the interface is considered as surface aggregation concentration (sac). If there are no spaces available for adsorption, they will form aggregate structures to orient their hydrophobic tails toward those of neighboring surfactant molecules and their hydrophilic head groups toward water. The concentration at which the surfactants start to form aggregation in solution as micelles is termed the cmc. One of the challenges in the study of aggregation properties, such as cmc, comes from the effects of specific ions and added salts on the aggregation properties of surfactants. It is accepted that the major effects of specific ions arises from counter ion interactions with surfactant head groups at relatively low to intermediate salt concentration. The effect of co-ion can become increasingly dominant as the added salt (containing co-ion) concentration increases [23-25]. To the best knowledge of the authors a comprehensive theory or model to adequately describe the effects of ion specificity and binding mechanism on surfactant aggregation properties has not been developed yet. In the present study, the corrosion inhibition efficiency (IE) of different mixtures of three homologous cationic surfactants of benzalkonium chlorides, C12Cl (or C12), C14Cl (or C14), and C16Cl (or C16), were investigated using electrochemical measurements. The sac, instead of cmc, is shown as a characteristic of monolayer formation at the electrodesolution interface. A new cmc and corrosion inhibition efficiency prediction model for ternary mixtures of homologous surfactants was developed. For cmc prediction, the model is simple, easy to apply, and has few assumptions. The inputs are a few cmc values of pure surfactants in solution without electrolyte and its outputs include cmc values of ternary mixed BAC at various mixed ratios over a wide range of background electrolyte concentration (up to 0.856 M NaCl). Based on the electrochemical measurement results and by incorporation of the Langmuir adsorption model, the corrosion inhibition efficiency over wide ranging conditions of relevant mixtures is accurately predicted.
Experimental Procedures and Materials
The surfactants used in this study are homologous cationic surfactants benzalkonium chlorides (BAC), including benzyl dimethyl dodecyl ammonium chloride (C12Cl), benzyl dimethyl tetradecyl ammonium chloride (C14Cl), and benzyl dimethyl hexadecyl ammonium chloride (C16Cl) with assay values higher than 99%. The test samples for surface tension measurements were prepared by sequential dilution of concentrated aqueous solutions of surfactants using double deionized water. The stock solution was prepared at a total surfactant concentration of 25 mm for electrochemical measurements using deionized water. A piece of X65 steel was used as the working electrode in electrochemical measurements with a surface area of 0.196 cm2. The composition (wt %) is C 0.06%, Mn 1.33%, P 0.007%, S 0.005%, Si 0.30%, Cu 0.30%, Ni 0.10%, V 0.022%, Cb 0.046%, Al 0.019%, Cr 0.05%, Mo 0.03%, Ti 0.017%, Ca 0.0033%, and Fe (balance). The surface of the X65 electrode was polished using SiC paper in the sequence of 400-600-800-1200 grit, followed by polishing using polishing cloth with a particle size of ~ 5 μm supplied by Buehler. A platinum ring electrode and a single junction saturated calomel electrode (SCE) were employed as counter and reference electrodes, respectively. Test solutions contained 0.171 or 0.599 M NaCl and were purged with Ar (>99.999%) for 2 hours (hr) to remove oxygen followed by a purge of CO2 (>99.999%) for 2 hr to ensure CO2 saturation prior to measurements. A flow of CO2 was maintained during the experiments to keep a positive pressure inside the cell to avoid air ingress. The pH was adjusted to 4 - 5 for different mixtures by the addition of 1.0 M NaHCO3 or diluted HCl. The surfactants were added at the beginning of each measurement. The test solutions were then kept at open circuit potential, Ecorr, for 2 hours for equilibration. Test conditions for different mixed surfactant systems are listed in Table 1. Testing System I is used as the primary example for the results discussion and inhibition efficiency prediction model derivation. Polarization resistance Rp was measured using the linear polarization resistance (LPR) method by polarizing the working electrode +/- 0.010 V (SCE) vs. Ecorr with a sweep rate of 0.1 mV/s. The slope of the tangent at the origin provided the value of Rp. Potentiodynamic scans were performed with a sweep rate of 1mV/s from -0.9 V (SCE) to -0.35 V (SCE). Electrochemical impedance spectroscopy (EIS) measurements were made with an applied alternating current (AC) potential of +/-0.010 V rms vs. Ecorr in the frequency range of 100,000 - 0.010 Hz. The direct current (DC) potential was set as zero relative to Ecorr. Each test was repeated at least three times as an independent measurement. The surface tension of test solutions was measured within a precision of 0.1 mn/m by the platinum ring setup, equipped with an isothermal vessel holder. All the measurements were performed at a constant temperature of 40 ± 0.2°C, which has been shown to be higher than the Kraft point of the surfactants and their mixtures in aqueous media containing various concentrations of NaCl. The constant temperature was maintained through a water circulation bath. The platinum ring was rinsed with water and heated to an orange color using a Bunsen burner between tests to ensure the complete removal of contaminants. Triplicate measurements were used to confirm reproducibility. All values of reported surface tension were determined through the aforementioned procedures (Table 1).
Table 1: Experimental condition for different testing systems.
| Testing system | Mixed molar ratio αi | Salt (M) | Measured cmc | T (°C) | pH | Rotation speed (RPM) |
|---|---|---|---|---|---|---|
| (C12Cl/C14Cl/C16Cl) | (μM) | |||||
| I | 0.70/0.25/0.05 | 0.171 | 144 | 40 | 4 | 300 |
| II | 0.33/0.33/0.33 | 0.599 | 16.5 | 40 | 5 | 100 |
Results and Discussion
Open circuit potential
The stability of open circuit potential, Ecorr, is important to electrochemical measurements. Examples of the dependence of Ecorr of X65 steel electrode on time in 0.171 M NaCl-containing aqueous media at 40°C are given in Figure 1. The Ecorr stabilized at around -0.725 V (SCE) without surfactant. Upon the addition of surfactant to the system of brine-containing media saturated with CO2, a positive shift of Ecorr is usually observed [26]. In the present research Ecorr is stabilized between -0.640 V (SCE) and -0.670 V (SCE) after the introduction of surfactants over a wide concentration range, which includes the sac and the cmc which is around 144 μm based on surface tension measurement as shown in Figure 2. Ecorr does not increase much at surfactant concentrations above the cmc. The difference in Ecorr in the absence and presence of surfactant indicates that the steel surface was covered and protected by the inhibitor adsorption. According to Riggs Jr [27], it is feasible to classify one inhibitor as anodic type or catholic type if the presence of inhibitor shifts Ecorr at least +85 mV or -85 mV, respectively, relative to Ecorr in the absence of inhibitor. However, the positive shift of Ecorr of the investigated System I at the highest concentration of 360 μm is only around 85 mV suggesting that both the dissolution of iron at the anode and the hydrogen evolution at the cathode were affected.
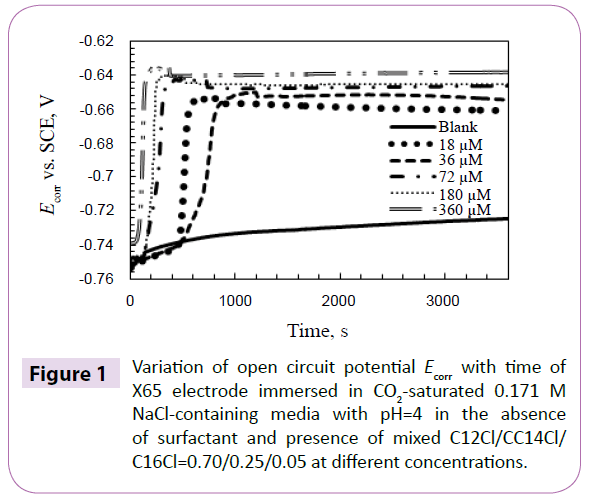
Figure 1: Variation of open circuit potential Ecorr with time of X65 electrode immersed in CO2-saturated 0.171 M NaCl-containing media with pH=4 in the absence of surfactant and presence of mixed C12Cl/CC14Cl/ C16Cl=0.70/0.25/0.05 at different concentrations.
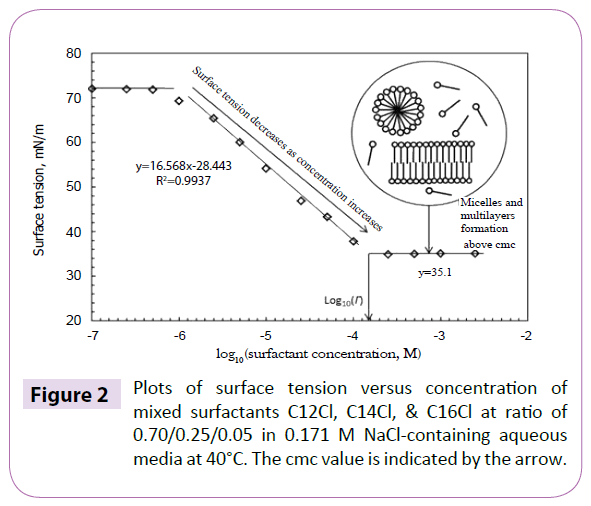
Figure 2: Plots of surface tension versus concentration of mixed surfactants C12Cl, C14Cl, & C16Cl at ratio of 0.70/0.25/0.05 in 0.171 M NaCl-containing aqueous media at 40°C. The cmc value is indicated by the arrow.
Potentiodynamic scan and linear polarization resistance measurement (LPR)
Potentio dynamic scans were performed on Testing System I with various concentrations of surfactants. The associated polarization curves are presented in Figure 3. Tafel slopes were estimated from these curves to calculate corrosion current density using the Tafel slope method [28]. The corrosion inhibition efficiency, IE (%), was calculated using Equation (1) .
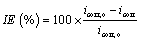 (1)
(1)
where icorr,o and icorr are the corrosion current density without and with corrosion inhibitors/surfactants in solution respectively. The polarization resistance was measured from LPR measurements and was then used to evaluate corrosion inhibition efficiency using Equation (2) with the Tafel slopes estimated from the curve of potentio dynamic scans.
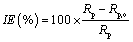 (2)
(2)
where Rp,o and Rp are polarization resistance in the absence and presence of corrosion inhibitors/surfactants respectively. The results of Tafel slopes polarization resistance, corrosion rate, polarization resistance, and inhibition efficiency are summarized in Table 2 for the Testing System I surfactant mixture. The corrosion inhibition efficiency results from potentio dynamic scans and LPR are very close. As can be seen, inhibition efficiency increases rapidly to around 90% with the increase in surfactant concentration up to 72 μm. Further increase in concentration does not effectively enhance inhibition efficiency even when the concentration is much higher than the cmc, Ccmc. The concentration of 72 μm is interpreted as the value of sac, Csac, at which a complete monolayer usually forms at the electrodesolution interface, and above which, bilayers or multilayers usually form at the electrode-solution interface [29,30]. As mentioned in the introduction section, corrosion inhibition is usually directly related to the electrode surface coverage. Therefore, the monolayer is much more effective with respect to corrosion protection and the formation of bilayers and multilayers do not contribute much to corrosion inhibition (Table 2 and Figures 1-3).
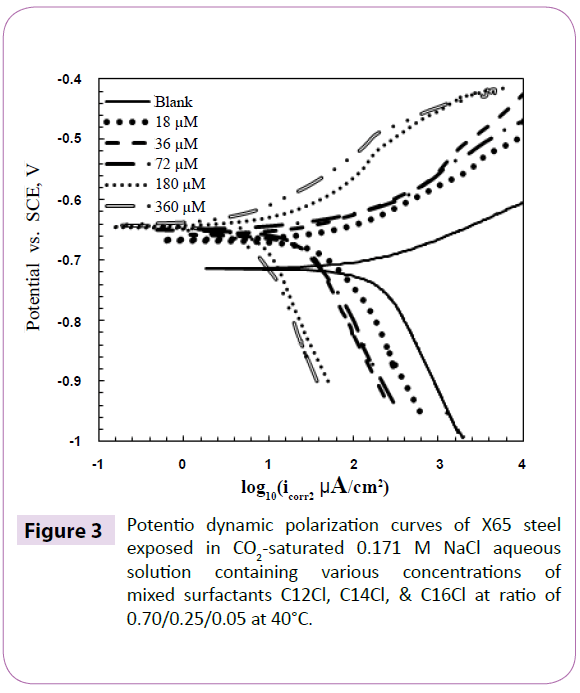
Figure 3: Potentio dynamic polarization curves of X65 steel exposed in CO2-saturated 0.171 M NaCl aqueous solution containing various concentrations of mixed surfactants C12Cl, C14Cl, & C16Cl at ratio of 0.70/0.25/0.05 at 40°C.
Table 2: Tafel slopes, corrosion rate, polarization resistance, and IE (%) for X65 in the absence and presence of Testing System I with different surfactant concentrations
| Total Concentration (μM) | βa (mV dec-1) | βc (mV dec-1) | icorr (μA cm-2) | IE (%)a | Rp (ohm·cm2) | IE (%)b |
|---|---|---|---|---|---|---|
| 0 | 61.5 | 255 | 202 | 0 | 104 | 0 |
| 9 | 65.7 | 248 | 118 | 42 | 188 | 44 |
| 18 | 67.1 | 243 | 89 | 56 | 249 | 58 |
| 36 | 68.3 | 235 | 53 | 74 | 436 | 76 |
| 54 | 63.2 | 245 | 34 | 83 | 643 | 83 |
| 72 | 64.8 | 239 | 26 | 87 | 845 | 88 |
| 100 | 61.7 | 238 | 13 | 94 | 1591 | 93 |
| 140 | 67.9 | 237 | 9 | 96 | 2550 | 96 |
| 180 | 61.6c | 245 | 7 | 97 | 2958 | 96 |
| 360 | 63.2d | 233 | 5 | 98 | 4282 | 98 |
aIE (%) calculated from potentiodynamic scans; bIE (%) calculated from LPR; c & dderived from the cathodic branch and βc due to lack of sensible linearity in the anodic branch in potentiodynamic scans as seen in Fig. 428.
Traditional modeling background
Corrosion inhibition assumes that the steel electrode corrodes uniformly and that the corrosion current density in the absence of surfactants, icorr,o, is usually represented by the total number of surface sites available for corrosion, whereas the corrosion current density in the presence of low concentration of inhibitor (usually lower than the cmc or sac), icorr, is represented by the number of uncovered surface sites remaining after limited surfactant adsorption [31]. Thus, the surface coverage θ is assumed to be the fraction of surface sites covered by surfactant adsorption relative to the total surface sites and can be given by the expression:
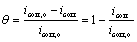 (3)
(3)
The adsorption of surfactants at the surface/interface is usually modeled by a traditional adsorption model. One of the widely accepted models is the Langmuir adsorption isotherm [32], in which the surface coverage is represented by:
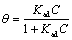 (4)
(4)
 (5)
(5)
Kad is given by
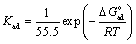 (6)
(6)
where Kad is equilibrium adsorption constant, C is the concentration of total surfactants in the bulk solution, the value 55.5 is the molar concentration of water in solution in moles per liter (M), 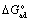 is the standard free energy of the adsorption process, R is gas constant, and T is absolute temperature. Note that for pure surfactant, C and Ccmc are total concentration of pure surfactant i, Ci, in solution and its corresponding cmc, Ccmc,i, respectively; for mixed surfactants, C and Ccmc are total concentration of mixed surfactants, Cmix, in solution and their corresponding mixed cmc, Ccmc,mix, respectively. A plot of (1/θ) vs. 1/C (for C < Ccmc) using Equation (5) based on EIS measurements for Testing System I yields an intercept which gives an equilibrium constant Kad of a value of 8.13 x 104 M-1, as shown in Figure 4. Ccmc represents the value of cmc. With Equation (6),
is the standard free energy of the adsorption process, R is gas constant, and T is absolute temperature. Note that for pure surfactant, C and Ccmc are total concentration of pure surfactant i, Ci, in solution and its corresponding cmc, Ccmc,i, respectively; for mixed surfactants, C and Ccmc are total concentration of mixed surfactants, Cmix, in solution and their corresponding mixed cmc, Ccmc,mix, respectively. A plot of (1/θ) vs. 1/C (for C < Ccmc) using Equation (5) based on EIS measurements for Testing System I yields an intercept which gives an equilibrium constant Kad of a value of 8.13 x 104 M-1, as shown in Figure 4. Ccmc represents the value of cmc. With Equation (6), 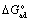 is calculated and the value is -39.8 kJ·mol-1. The negative value demonstrates that the adsorption of surfactant on the steel surface is a spontaneous process and shows a strong interaction between surfactant molecules and steel surface [32]. Generally, if adsorption free energy is more positive than -20 kJ·mol-1, the interaction between surfactant and metal is classified as physisorption due to electrostatic interaction. When the adsorption free energy is more negative than -40 kJ·mol-1, the adsorption involves charge sharing or transfer between surfactant molecules and metal surface to form coordination bonds, which is also classified as chemisorption [33]. Based on the calculated value of adsorption free energy, -39.8 kJ·mol-1, the adsorption mechanism of the discussed mixture can be classified as the combination of chemisorption and physisorption. Specifically, the adsorption mechanism of surfactant on steel electrode surface is often interpreted as follows: the unpaired or π electrons of the surfactant molecule and the vacant d orbitals of iron share electrons (chemisorption); the charged surfactant and electrode surface interact through electrostatic force (physisorption).
is calculated and the value is -39.8 kJ·mol-1. The negative value demonstrates that the adsorption of surfactant on the steel surface is a spontaneous process and shows a strong interaction between surfactant molecules and steel surface [32]. Generally, if adsorption free energy is more positive than -20 kJ·mol-1, the interaction between surfactant and metal is classified as physisorption due to electrostatic interaction. When the adsorption free energy is more negative than -40 kJ·mol-1, the adsorption involves charge sharing or transfer between surfactant molecules and metal surface to form coordination bonds, which is also classified as chemisorption [33]. Based on the calculated value of adsorption free energy, -39.8 kJ·mol-1, the adsorption mechanism of the discussed mixture can be classified as the combination of chemisorption and physisorption. Specifically, the adsorption mechanism of surfactant on steel electrode surface is often interpreted as follows: the unpaired or π electrons of the surfactant molecule and the vacant d orbitals of iron share electrons (chemisorption); the charged surfactant and electrode surface interact through electrostatic force (physisorption).
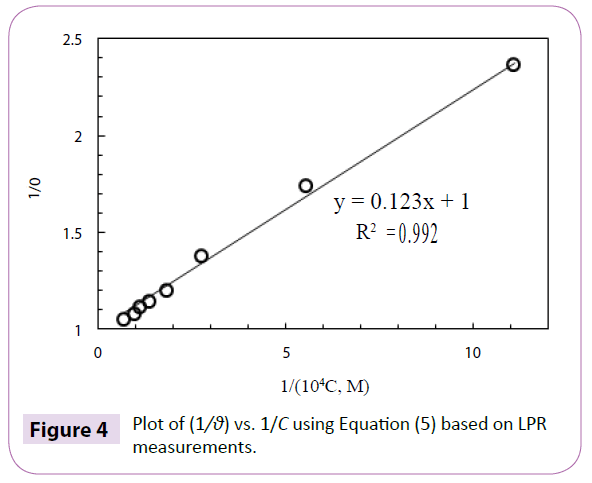
Figure 4: Plot of (1/θ) vs. 1/C using Equation (5) based on LPR measurements.
IE prediction model using cmc
A combination of Equations (3) and (4) and rearrangement lead to a useful equation that correlates the corrosion current density to surfactant concentration [34]:
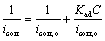 (7)
(7)
There should be a linear relationship between the inverse of corrosion current density (1/icorr) and bulk surfactant concentration C when C ≤ Csac. The surfactant adsorption and corrosion inhibition at this level is particularly effective with increasing concentration due to plenty of active surface sites available to be covered by surfactants. Above the sac, an abrupt transition should occur in the slope, because the electrode surface is covered by a complete monolayer. Increasing concentration of the surfactant above the sac should lead to the formation of bilayers/multilayers and micelles (above cmc), which slightly contribute to surface coverage and corrosion inhibition. Thus, the sac is an important scaling factor in the determination of the effect of surfactant concentration on adsorption and corrosion inhibition. However, because the cmc is easier to measure than the sac in the present research and due to the availability of a developed prediction model for cmc, the concentration in Equation (7) is normalized by dividing by Ccmc, rather than by Csac, and rearranged to give:
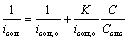 (8)
(8)
where K is equal to the adsorption constant Kad multiplied by Ccmc of surfactant. Further rearrangement leads to a general form which can be used to evaluate corrosion of a variety of surfactants under a variety of test conditions:
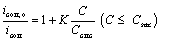 (9)
(9)
Note homologous surfactants tend to achieve similar levels of surface coverage at similar ratios of surfactant concentration to surfactant cmc, so the value of K does not vary a lot for homologous surfactants. Note that C could increase above the sac or the cmc, but the fitting is generally not as good as the fitting for C below the sac. The measured cmc for the mixture, 0.70/0.25/0.05 in 0.171M NaCl aqueous media at 40°C, is 144 μm. A plot of 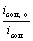 versus
versus 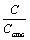 yields a slope of constant K=13.74, and an intercept of 1 which is in the absence of inhibitor, as shown in Figure 5. It is also seen in Figure 5 there is one abrupt transition around the concentration of the sac, which indicates that when the inhibitor concentration is below the sac, inhibition efficiency increases rapidly with the increases in concentration; above the sac, the increase in concentration does not contribute much to further inhibition efficiency increase. The cmc prediction model and inhibition efficiency prediction model were validated by performing tests on mixed surfactant C12Cl/C14Cl/C16Cl = 0.33/0.33/0.33 with 0.599 M NaCl. Figure 6 illustrates a good agreement between predicted inhibition efficiency and experimental inhibition efficiency.
yields a slope of constant K=13.74, and an intercept of 1 which is in the absence of inhibitor, as shown in Figure 5. It is also seen in Figure 5 there is one abrupt transition around the concentration of the sac, which indicates that when the inhibitor concentration is below the sac, inhibition efficiency increases rapidly with the increases in concentration; above the sac, the increase in concentration does not contribute much to further inhibition efficiency increase. The cmc prediction model and inhibition efficiency prediction model were validated by performing tests on mixed surfactant C12Cl/C14Cl/C16Cl = 0.33/0.33/0.33 with 0.599 M NaCl. Figure 6 illustrates a good agreement between predicted inhibition efficiency and experimental inhibition efficiency.
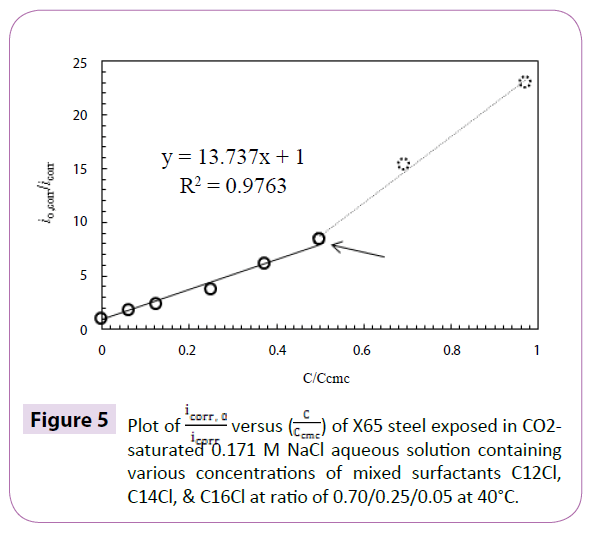
Figure 5: Plot of  versus
versus 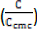 of X65 steel exposed in CO2- saturated 0.171 M NaCl aqueous solution containing various concentrations of mixed surfactants C12Cl, C14Cl, & C16Cl at ratio of 0.70/0.25/0.05 at 40°C.
of X65 steel exposed in CO2- saturated 0.171 M NaCl aqueous solution containing various concentrations of mixed surfactants C12Cl, C14Cl, & C16Cl at ratio of 0.70/0.25/0.05 at 40°C.
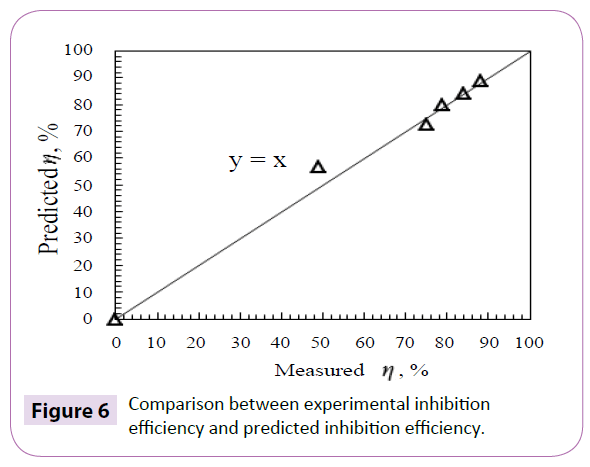
Figure 6: Comparison between experimental inhibition efficiency and predicted inhibition efficiency.
Effect of Salt on Surfactant Aggregation
Despite extensive progress in theoretical and experimental work has been made in the study of aggregation properties of ionic surfactants the effect of added salt and specific ion (dissociated from surfactants and salt) is still a challenge [35-38]. The ion and salt usually shift cmc, aggregation number of micelle, sphere-torod transition, and counter ion binding coefficient [39,40]. The micelle shape, micelle composition (for mixed surfactants), and micelle distribution are also affected. In the present work an improved model based on existing molecular thermodynamic theory has been applied to various pure and mixed surfactants. Activities of monomeric surfactant and counter ion, which are evaluated from Setchenov equation [41] and [42,43] states the equation respectively, are incorporated in the model. The specific head group-counter ion pair is introduced to (Figures 4-6) model counter ion specificity. The counter ion binding coefficient is initially set as a variable and finds its optimal value by minimizing micellization free energy. The effect of coion is reflected from salt-dependent factors, including Setchenov coefficient ks, dielectric decrement of salt δs, and the correlation between surface tension and salt concentration of aqueous solution dσo/ dCs. The developed model has been applied to pure anionic & cationic surfactants in aqueous solution containing various salt concentrations for validation. Assuming the monomeric surfactant mi (i=1, 2, or 3...) is completely dissociated in aqueous solution containing counter ion mj (j=1, 2, or 3…) but in the micelle form the surfactant is associated to some extent with counter ions, therefore, the surfactant micellization is described by the following process [29,30,44,45]
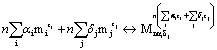 (10)
(10)
where αi is the composition of surfactant i in the micelle, Mnαiδj, which has an aggregation number n, micelle composition αi, and a counter ion binding coefficient δj. For micelles of pure surfactant, αi = 1; for mixed micelles, 0 < αi < 1. zi and zj are the valences of ionic surfactant i in dissociated form and counter ion j. For nonionic surfactant i, zi = 0 and δj = 0. By the consideration of activity coefficient, the chemical potential of micelle Mnαiδj, monomeric surfactant i, and counter ion j in solution can be written, respectively, as
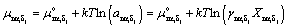 (11)
(11)
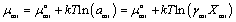 (12)
(12)
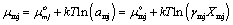 (13)
(13)
where 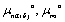 and
and  are the standard chemical potentials of micelle, monomeric surfactant, and counter ion in solution, respectively. The standard state of water is defined as pure liquid while the standard state of all other species is defined for an infinitely dilute solution.
are the standard chemical potentials of micelle, monomeric surfactant, and counter ion in solution, respectively. The standard state of water is defined as pure liquid while the standard state of all other species is defined for an infinitely dilute solution. 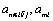 and
and 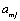 are the corresponding activities.
are the corresponding activities. 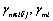 and
and 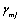 are the corresponding activity coefficients. Micelle is treated as one separated phase from aqueous solution and thus
are the corresponding activity coefficients. Micelle is treated as one separated phase from aqueous solution and thus 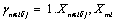 and
and 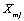 are mole fractions of micelle, monomeric surfactant, and counter ion in bulk solution. The cmc is assumed to be equal to monomer concentration Xm (here this is the mole fraction) and is calculated by [29,30]
are mole fractions of micelle, monomeric surfactant, and counter ion in bulk solution. The cmc is assumed to be equal to monomer concentration Xm (here this is the mole fraction) and is calculated by [29,30]
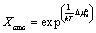 (14)
(14)
The micellization free energy Δμmo is estimated from a few contributing terms as described below:
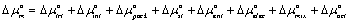 (15)
(15)
where 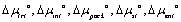 and
and 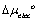 are the free energy contributions from hydrocarbon transfer from water into micelle, formation of micellar core-water interface, hydrocarbon tail packing in the micelle, surfactant head group steric interaction, head group counter ion mixing, and electrostatic interaction, respectively [35-38].
are the free energy contributions from hydrocarbon transfer from water into micelle, formation of micellar core-water interface, hydrocarbon tail packing in the micelle, surfactant head group steric interaction, head group counter ion mixing, and electrostatic interaction, respectively [35-38]. 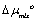 reflects the entropy of forming a micelle with surfactant composition of αi (equal to 1 for pure surfactant) in the bulk solution.
reflects the entropy of forming a micelle with surfactant composition of αi (equal to 1 for pure surfactant) in the bulk solution. 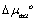 comes from the activity contribution. Free energy micellization as a function of variables, including on micelle shape S, micelle composition αi (i represents surfactant), micellar core minor radius lc, and counter ion binding coefficient δj (j represents ion), at given solution conditions is minimized using home-designed Matlab code. The minimized micellization free energy is then used for the evaluation of cmc, aggregation number, counter ion binding coefficient, and sphereto- rod transition. Details of cmc model derivation and free energy calculation is reported elsewhere. The model is applied to pure anionic surfactants, alkali metal dodecyl sulfate XDS, in aqueous solution with various added salts XCl (X=Li+, Na+, K+, and Cs+) to examine counter ion effect, as shown in Figure 7 which presents the model prediction (various lines) and experimental data (various symbols) of cmc and weight-based aggregation number nw. The predicted cmc agrees well with experiment at low to medium salt concentration (~1M). Slight deviation is observed above the salt concentration of 1 M as shown in Figure 7a. The sphere-to-rod transition which is interpreted as the sharp up-turn of nw as a function of salt concentration is clearly seen in Figure 7b. The predicted nw and experimental nw match reasonably well. The slightly underestimated nw before the sphere-to-rod transition is attributed to the globular structure of surfactant aggregates, rather than regular spherical micelles, and the fact that the model does not incorporate globular micelle. The Hofmeister series, which is Li+ < Na+ < K+ < Cs+ for anionic surfactants [39,40], is correctly reflected by the effect of counter ion on the depression of cmc, and on the increment of aggregation number of alkali metal alkyl sulfates. The model is also applied to pure alkyl trim ethyl ammonium surfactant CnTABr in solution with added salt (NaBr, NaCl, or KCl) to evaluate chain length effects, counter ion effects, and coion effects on aggregation properties as shown in Figure 8. The cmc (Figure 8a) and sphere-to-rod transition threshold (Figure 8b) decreases as chain length increases whereas nw (Figure 8b) increases as chain length increases. The predicted cmc for all surfactants in Figure 8 match very well with the experiment except that slight deviation appears for C12TABr with added NaBr above 1 M. excellent agreement is observed between predicted and experimental nw.
comes from the activity contribution. Free energy micellization as a function of variables, including on micelle shape S, micelle composition αi (i represents surfactant), micellar core minor radius lc, and counter ion binding coefficient δj (j represents ion), at given solution conditions is minimized using home-designed Matlab code. The minimized micellization free energy is then used for the evaluation of cmc, aggregation number, counter ion binding coefficient, and sphereto- rod transition. Details of cmc model derivation and free energy calculation is reported elsewhere. The model is applied to pure anionic surfactants, alkali metal dodecyl sulfate XDS, in aqueous solution with various added salts XCl (X=Li+, Na+, K+, and Cs+) to examine counter ion effect, as shown in Figure 7 which presents the model prediction (various lines) and experimental data (various symbols) of cmc and weight-based aggregation number nw. The predicted cmc agrees well with experiment at low to medium salt concentration (~1M). Slight deviation is observed above the salt concentration of 1 M as shown in Figure 7a. The sphere-to-rod transition which is interpreted as the sharp up-turn of nw as a function of salt concentration is clearly seen in Figure 7b. The predicted nw and experimental nw match reasonably well. The slightly underestimated nw before the sphere-to-rod transition is attributed to the globular structure of surfactant aggregates, rather than regular spherical micelles, and the fact that the model does not incorporate globular micelle. The Hofmeister series, which is Li+ < Na+ < K+ < Cs+ for anionic surfactants [39,40], is correctly reflected by the effect of counter ion on the depression of cmc, and on the increment of aggregation number of alkali metal alkyl sulfates. The model is also applied to pure alkyl trim ethyl ammonium surfactant CnTABr in solution with added salt (NaBr, NaCl, or KCl) to evaluate chain length effects, counter ion effects, and coion effects on aggregation properties as shown in Figure 8. The cmc (Figure 8a) and sphere-to-rod transition threshold (Figure 8b) decreases as chain length increases whereas nw (Figure 8b) increases as chain length increases. The predicted cmc for all surfactants in Figure 8 match very well with the experiment except that slight deviation appears for C12TABr with added NaBr above 1 M. excellent agreement is observed between predicted and experimental nw.
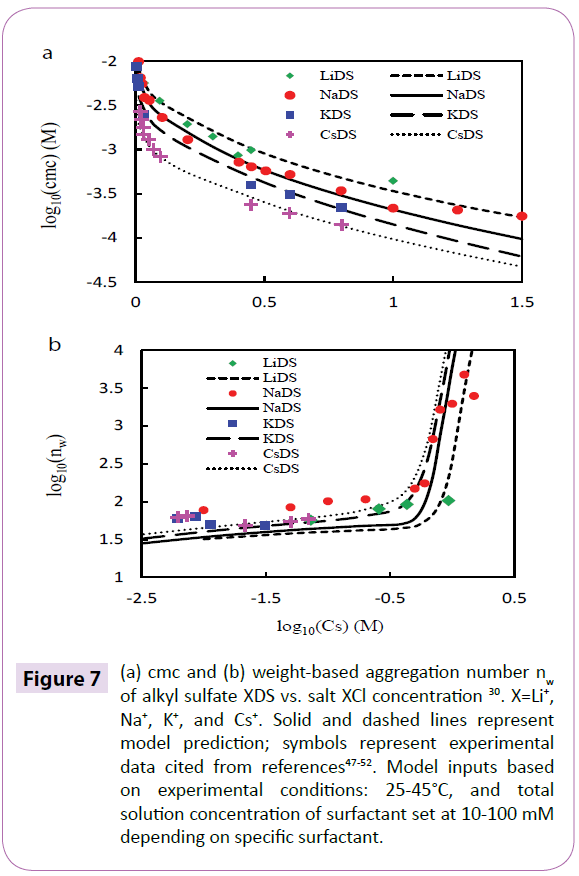
Figure 7: (a) cmc and (b) weight-based aggregation number nw of alkyl sulfate XDS vs. salt XCl concentration 30. X=Li+, Na+, K+, and Cs+. Solid and dashed lines represent model prediction; symbols represent experimental data cited from references47-52. Model inputs based on experimental conditions: 25-45°C, and total solution concentration of surfactant set at 10-100 mM depending on specific surfactant.
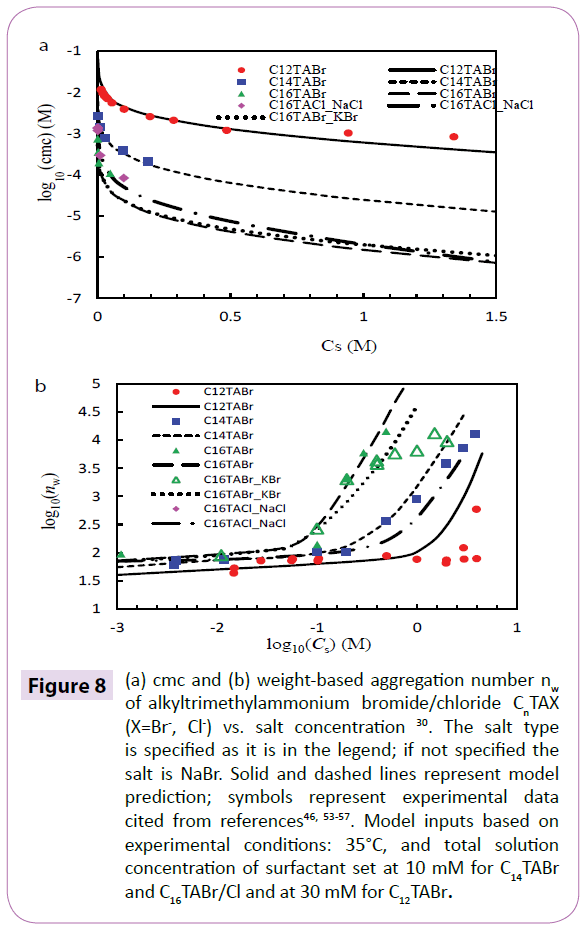
Figure 8: (a) cmc and (b) weight-based aggregation number nw of alkyltrimethylammonium bromide/chloride CnTAX (X=Br-, Cl-) vs. salt concentration 30. The salt type is specified as it is in the legend; if not specified the salt is NaBr. Solid and dashed lines represent model prediction; symbols represent experimental data cited from references46, 53-57. Model inputs based on experimental conditions: 35°C, and total solution concentration of surfactant set at 10 mM for C14TABr and C16TABr/Cl and at 30 mM for C12TABr.
The transition threshold of salt concentration is well predicted as indicated by the change of nw. For C16TABr with KBr for example, the predicted threshold is 0.08 M and the experimental threshold is 0.1 M46(Figures 7a-8b) [46-52].
Conclusions
Corrosion inhibition efficiency rapidly increases as the surfactant concentration increases to the sac, indicating the formation of a relatively complete surfactant monolayer around the sac that effectively protects the steel electrode from corrosion. There is excellent agreement among inhibition efficiency measured from potentio dynamic scans and LPR. A new cmc prediction model for various pure and mixed surfactants is developed over a wide concentration range of salt. The improved corrosion inhibition efficiency prediction model which incorporates the cmc prediction is an effective method that can be used for corrosion inhibition prediction of various ternary mixtures of homologous BAC surfactants at various salt concentrations. The corrosion inhibition model presented in this work provides a potential method to evaluate cmc and corrosion inhibition efficiency of binary-, ternary-, or multiple-component mixtures of surfactants of interest in the presence of salt in solution.