Keywords
Impedance measurements; Kramers-Kronig; Fast Fourier Transform; PEFC
Introduction
Electrochemical impedance spectroscopy (EIS) is a powerful technique that can be applied in-situ to de-convolute the various loss mechanisms in polymer electrolyte fuel cells (PEFCs) that occur at different rates. EIS measurements are commonly represented in a Nyquist plot where the data are represented as a locus of points and each data corresponds to a different measurement frequency. The use of electrical equivalent circuits with the experimental EIS technique is a well-established methodology to interpret the electrochemical mechanisms represented in the Nyquist plot. Before attempting to apply or fit electrical equivalent circuits with experimental EIS measurements using a non-linear regression method, an evaluation of the validity of the EIS data has to be carried out using Kramers-Kronig (K-K) relations. These relations are mathematical properties that relate the real and imaginary part of the frequency response resulting from the electrochemical system studied [1] K-K relations are applied to electrochemical systems whose frequency response is linear, causal and stable. If the experimental imaginary components of the impedance response of an electrochemical system do not coincide with the transformed imaginary components, nor the experimental real components with the transformed real components then the experimental data are not obtained under either a causal system (the measured impedance response is due only to the AC perturbation applied), linear system (for small AC perturbations) or stable system (the system returns to its original state after the perturbation is removed and does not change with time) [2].
K-K transformations have been derived from the Cauchy’s Integral Theorem [2] which defines the integral around a closed contour and evaluates the real part or imaginary part of the impedance at a particular frequency with a pole ω created in the real axis of the frequency domain. Although K-K relations are a reliable method of evaluating the validity of EIS measurements, the method has often been neglected due to the complexity of applying the mathematical K-K relations to real-world impedance measurements. VanderNoot [3] reported that it is possible to evaluate the K-K relations to EIS data using the Fast Fourier Transform (FFT) and the Hilbert transformation of impedance data. In this study, the validity of experimental impedance measurements in PEFCs is evaluated through a computationalalgorithm developed from FFT theory, the Hilbert transformation method reported by VanderNoot [3] and the impedance model of PEFCs reported in the authors’ previous study [4] The impedance model taken as a baseline was derived from electrochemical theory, and complies with linearity, stability and causality properties for Kramers-Kronig transformation [4] This study also demonstrates that the impedance model from the authors’ previous study can not only be applied to estimate the electrochemical mechanisms during PEFC operation but also can assist in the development of algorithms to evaluate correctness in experimental EIS data. A script developed in Matlab® as shown in Appendix enables the application of the computational algorithm developed in this study with real-world experimental EIS data. Once the computational algorithm has been developed, it will be applied to EIS measurements of PEFCs to demonstrate the most common factors that affect the validity of EIS measurements. Some commercial softwares such as Zview, ZMan, etc. allows the evaluation of EIS data through K-K relations. However K-K analysis through commercial software requires expensive frequency response analysers (FRAs) for EIS data measurement. Although the computational algorithm in this study was developed as a script in Matlab® software, it can be created and applied as a standalone executable file without Matlab software [5] Another advantage is that it does not require expensive experimental equipment for EIS data evaluation and can be used within lowcost FRAs [6].
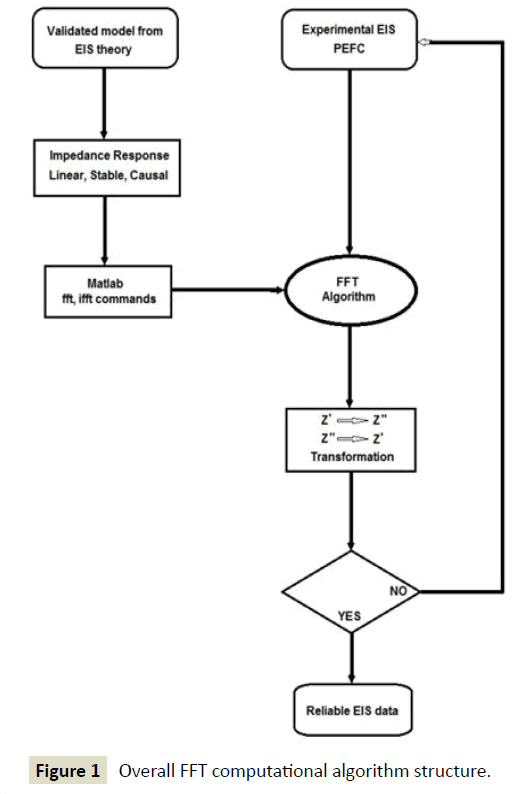
FFT Computational Algorithm Structure
The overall framework developed for the FFT computational algorithm is illustrated in Figure 1 the frequency response of the validated impedance model developed in the authors’ previous study [4] which complies with linearity, stability and causality properties is taken as a baseline to assist with the development of the FFT computational algorithm. The FFT numerical method is applied to experimental EIS data carried out in PEFCs using a script developed in Matlab®. The evaluation of data transformation (real to imaginary Z’→Z’’ and imaginary to real Z’’→Z’) and hence validity of the impedance measurements can identify the factors that lead to incorrect EIS measurements. A lack of consistency in data transformation represents EIS measurements carried out in a PEFC under nonlinear, unstable or no causal conditions.
Figure 1 Overall FFT computational algorithm structure.
Impedance Model to assist FFT computational algorithm development
The validity of experimental EIS data can be indirectly evaluated using a correct model which satisfies linearity, stability and causality. If a correct model which satisfies such conditions is fitted to experimental EIS measurements and a good fit is observed then the experimental data are correct and truly represent the electrochemical mechanisms of the electrochemical system. Nevertheless a poor fit can be a result of invalid experimental EIS data. In the authors’ previous study [4], an impedance model based on electrochemical theory was developed and fitted to experimental EIS measurements carried out in a 25 cm2 H2/ air PEFC operated at 0.12 A/cm2. The operational temperature was 50oC and the back gas pressure was held to 0.9 bar(g) for both the anode and cathode. Flow rates were held constant during all the experiments, hydrogen to the anode was supplied at a stoichiometry of 2 and air to the cathode supplied at a stoichiometry of 2.5. The PEFC was operated with 98% hydrogen relative humidity (RH) in the anode and 55% RH in the cathode. The frequency scan was performed from 20 kHz down to 0.1 Hz, with an alternating voltage signal and 10 mV amplitude.
The impedance response of the model is defined as (1)

with 
where RP is the resistance to the flow of ions in the electrolytic phase of the cathode catalyst layer (CCL); RC represents the charge transfer resistance presented in the oxygen reduction reaction (ORR) and is defined as  where b is the Tafel slope, ηS represents a value of voltage in activation over potential, and j0 is the exchange current;
where b is the Tafel slope, ηS represents a value of voltage in activation over potential, and j0 is the exchange current;  is defined as the Warburg impedance and describes diffusion across a finite dimension in the frequency domain [7], with
is defined as the Warburg impedance and describes diffusion across a finite dimension in the frequency domain [7], with  defined as resistance for the diffusion process and
defined as resistance for the diffusion process and  D defined as the time constant to diffuse oxygen through the CCL; Y represents a parameter related to capacitance, superscript P represents a parameter to correct the inhomogeneity in the distribution of charge between the electrode-electrolyte inteface; ω is the angular frequency; i is the imaginary component in impedance; Re represents the total ohmic resistance to flow of electrons and ions in the bipolar plate, gas diffusion layer (GDL) and polymer electrolyte membrane (PEM); x represents the thickness of the CCL (dimensionless) and for EIS measurements is equal to 1. Equation 1 was fitted to the EIS measurements of a 25 cm2 H2/air PEFC operated at 0.12 A/cm2 and the resulting parameters are shown in Table 1.
D defined as the time constant to diffuse oxygen through the CCL; Y represents a parameter related to capacitance, superscript P represents a parameter to correct the inhomogeneity in the distribution of charge between the electrode-electrolyte inteface; ω is the angular frequency; i is the imaginary component in impedance; Re represents the total ohmic resistance to flow of electrons and ions in the bipolar plate, gas diffusion layer (GDL) and polymer electrolyte membrane (PEM); x represents the thickness of the CCL (dimensionless) and for EIS measurements is equal to 1. Equation 1 was fitted to the EIS measurements of a 25 cm2 H2/air PEFC operated at 0.12 A/cm2 and the resulting parameters are shown in Table 1.
| ReΩ.cm2 |
RP Ω.cm2 |
Y CPE×10-3sPΩ.cm2 |
P |
RC Ω.cm2 |
RW Ω.cm2 |
TW s |
| 0.24 |
0.18 |
8.836 |
0.9112 |
0.9975 |
0.16 |
0.0920 |
Table 1: Resulting parameters from fitting Eq. 1 to EIS measurements.
In this study, the simulated impedance response from Equation 1 using parameters in Table 1 will be taken into account to assist with the development of the FFT numerical method. Once the FFT computational algorithm is developed, it will be applied to experimental EIS measurements of different PEFCs to demonstrate the most typical factors than can lead to invalid EIS data.
FFT computational algorithm development
Experimental EIS measurements are commonly carried out through the use of frequency response FRAs. FRAs use an orthogonal system that involves sines and cosines to determine the complex impedance of a single-frequency input signal. The resulting impedance response is calculated through mathematical transformations of Fourier transform (FT) analysis. The discrete FT (DFT) changes the time domain discrete data into the frequency domain discrete data. The FFT is referred to as a fast computerized implementation of the DFT. This section demonstrates that it is possible to calculate the imaginary component Z’’ from the real component Z’ and vice versa and evaluate the validity of EIS measurements using the FFT computational algorithm. FFT provides a fast and efficient algorithm of computation of the frequency domain. Nowadays, the FFT algorithm used to compute the DFT has been developed and implemented in commercial software such as Matlab®.
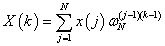 (2)
(2)
with 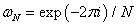
Equation 2 represents the DFT of a signal with a sequence of k=0…N, where x(j) is the nth input sample (j=1…N); and N is the number of samples. The command fft in Matlab® returns the DFT of a vector x with a length N, computed with a FFT algorithm.
The inverse discrete FT (IDFT) changes the frequency domain data into the time domain data and its algorithm computed by FFT has also been implemented in Matlab®:
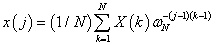
With 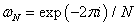 (3)
(3)
Where X(k) is the kth harmonic (k=1...N); The command ifft in Matlab® calculates the IDFT of a vector X computed through FFT.
EIS measurements are commonly represented in logarithm space data. The FFT algorithm requires measurements with linearly spaced frequencies. The equation reported by Papoulis [8] calculates a new frequency range based on a reference frequency, as such:
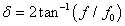 (4)
(4)
Where δ is the new calculated frequency range, f is the measured frequency and f0 is the reference frequency and in this study corresponds to the frequency where the imaginary part Z’’ of EIS measurements reaches its minimum value.
Imaginary to real transformation Z’’→Z’: Once the new frequency range δ has been calculated from the experimental measured frequency, the imaginary components Z’’ of the impedance response to be evaluated (in this case the impedance response from Equation 1 using the parameters in Table 1 are interpolated with a frequency range from zero to π, with 1024 equal points, as the number of data for FFT analysis has to be a power of two. The causality property for the frequency response of an electrochemical system implies that the frequency response to an AC perturbation cannot precede the input AC perturbation [2] In the frequency response of a causal system, the real component is an even function of the frequency and the imaginary component is an odd function of the frequency, as such  ,
,  . The following procedure is developed in a script in Matlab® (see Appendix) to calculate the real components from imaginary components (Z’’→Z’ transformation).
. The following procedure is developed in a script in Matlab® (see Appendix) to calculate the real components from imaginary components (Z’’→Z’ transformation).
1. In FFT analysis both positive and negative frequencies have to be considered. Due to the fact that the imaginary component is an odd function of the frequency to comply with the causality property, the imaginary components (in this case from the impedance response from Equation 1 using the parameters in Table 1) at negative frequencies are calculated and concatenated with the ones at positive frequencies as shown in Figure 2a.
2. The FFT is applied to the imaginary interpolated data shown in Figure 2a using the command fft in Matlab® and without considering the imaginary unit i; as a result complex numbers are calculated.
Figure 2 Z’’→Z’ transformation in impedance response a) Interpolated imaginary component, b) transformed real component.
3. The resulting data at positive frequencies are set to be zero.
4. The complex conjugates of the data at negative frequencies resulting from step 2 are calculated, doubled and concatenated with the data gathered in step 3.
5. The inverse FFT ifft(i.x,dim) in Matlab®, where i is imaginary unit, x is the vector of data to be transformed and dim is the dimension of the transformation and is equal to 2048, is applied to the set of data gathered in step 4 to calculate the real components at positive and negative frequencies. Figure 2b represents the transformed real components at positive frequencies at the logarithm scale (f/f0).
Real to imaginary transformation Z’→Z’’: The following procedure is developed in a script in Matlab® (see Appendix) to calculate the imaginary components from real components (Z’→Z’’ transformation).
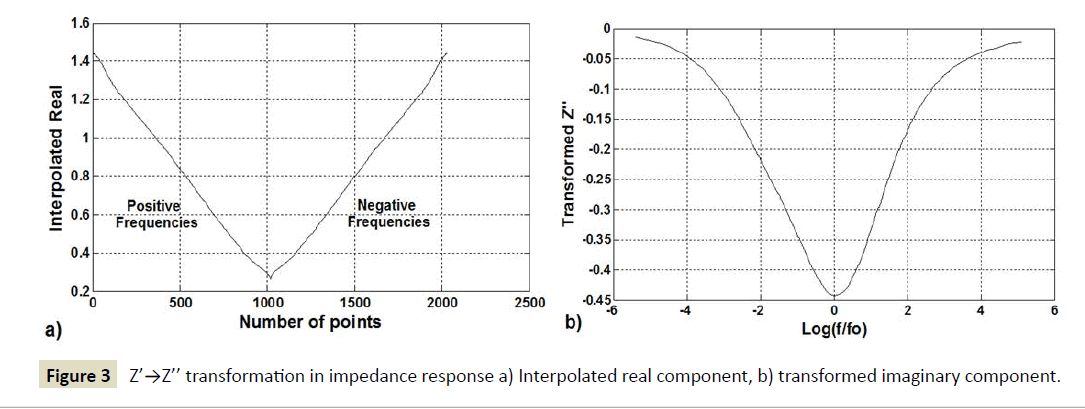
1. The real components Z’ of the impedance response to be evaluated (in this case the impedance response from Equation 1 using the parameters in Table 1) are interpolated with a frequency range from zero to π, with 1024 equal points. The interpolated real components at negative frequencies are calculated and concatenated with the ones at positive frequencies due to the fact that the real component is an even function of the frequency, as shown in Figure 3a. Note that Figure 3a is also the result of step 5 as discussed in the previous Z’’→Z’ transformation section.
Figure 3 Z’→Z’’ transformation in impedance response a) Interpolated real component, b) transformed imaginary component.
2. The FFT is applied to the data shown in Figure 3a using the command fft in Matlab® and complex numbers are generated.
3. The data at negative frequencies are set to be zero.
4. The complex conjugates of the data at positive frequencies resulting from step 2 are calculated, doubled and concatenated with the data gathered in step 3.
5. The inverse FFT ifft(i.x,dim) in Matlab®, where i is imaginary unit, x is the vector of data to be transformed and dim is the dimension of the transformation and is equal to 2048, is applied to the data gathered in step 4 to calculate the imaginary components at positive and negative frequencies. This results in the imaginary components shown in Figure 2a. Figure 3b represents the calculated imaginary components at positive frequencies plotted at the logarithm scale (f/fO).
EIS data transformation using FFT computational algorithm
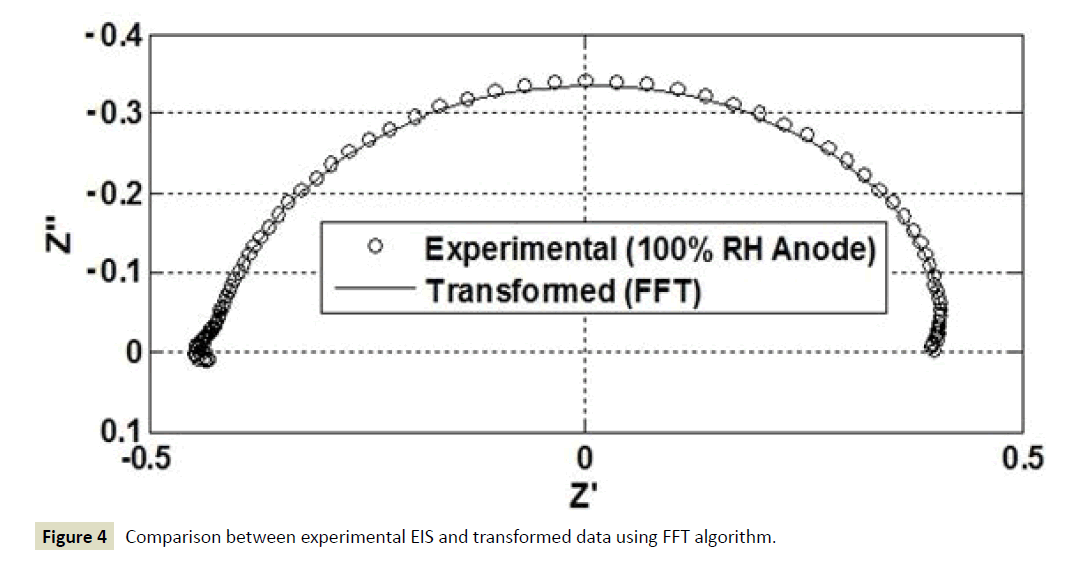
This section demonstrates the application of the FFT algorithm developed in the previous section 2.2. with EIS data. The computational algorithm was written as a script in Matlab®. This is shown in Appendix. It requires a vector for the range of frequencies applied during the EIS measurements. A vector for the experimental real component and a vector for the experimental imaginary component of the EIS data are required in the Matlab script as well. As an example of how to carry out data transformation Z’→Z’’, Z’’→Z’ from EIS data and hence validity of impedance measurements, the FFT computational algorithm shown in Appendix is applied to EIS measurements carried out in a 25 cm2 H2/air PEFC operated at 0.23 A/cm2 with 100% RH in the hydrogen supplied to the anode and dry air supplied in the cathode. The operating temperature was 50oC. EIS measurements were carried from 10 kHz to 0.1 Hz. Figure 4 shows a comparison between the experimental data and the transformed data Z’→Z’’, Z’’→Z’ using the FFT computational algorithm shown in the Appendix. The transformed imaginary and transformed real data obtained from the FFT are calculated from the new frequency range δ expressed in Equation 4 where f0 is the centre frequency for the range of data to be transformed and corresponds to the frequency where the imaginary component Z’’of EIS measurements reaches its minimum value. The real component calculated from FFT is zero at the reference frequency f0. The real components Z’ of the experimental data were shifted to be zero where the imaginary component Z’’ reaches its minimum value. This modification in the experimental data allowed the comparison with the transformed data from FFT, as shown in Figure 4. This data modification (real component shifted to be zero where the imaginary component Z’’ reaches its minimum value has been considered in the script shown in Appendix to compare experimental EIS measurements with data transformation through the FFT algorithm. The results shown in Figure 4 demonstrate that the experimental EIS measurements satisfies real to imaginary Z’→Z’’ and imaginary to real Z’’→Z’ data transformation and therefore comply with linearity, stability and causality properties and truly represent the frequency response of the electrochemical mechanisms of the PEFC to the AC perturbation. In the next sections the FFT computational algorithm will be applied to other experimental EIS measurements of PEFCs to demonstrate the factors that cause invalid EIS data.
Figure 4 Comparison between experimental EIS and transformed data using FFT algorithm.
Application of FFT Computational Algorithm on PEFC EIS Measurements
One key advantage of the EIS technique is that it is non-invasive and can be applied in-situ. Another advantage is that the frequency response tests are simple to carry out and can be easily tuned for greater accuracy by using readily-available sinusoidal generators and precise measuring equipment. However, an evaluation of the validity of the measured EIS data will ensure that the physical mechanisms of an electrochemical system will be truely represented in the Nyquist plot. In this section the most common factors that lead to incorrect data transformation Z’→Z’’, Z’’→Z’ and invalid EIS measurements are discussed by applying the algorithm shown in the Appendix to different EIS measurements in PEFCs.
Analysis of inductance effect on EIS measurements of PEFCs
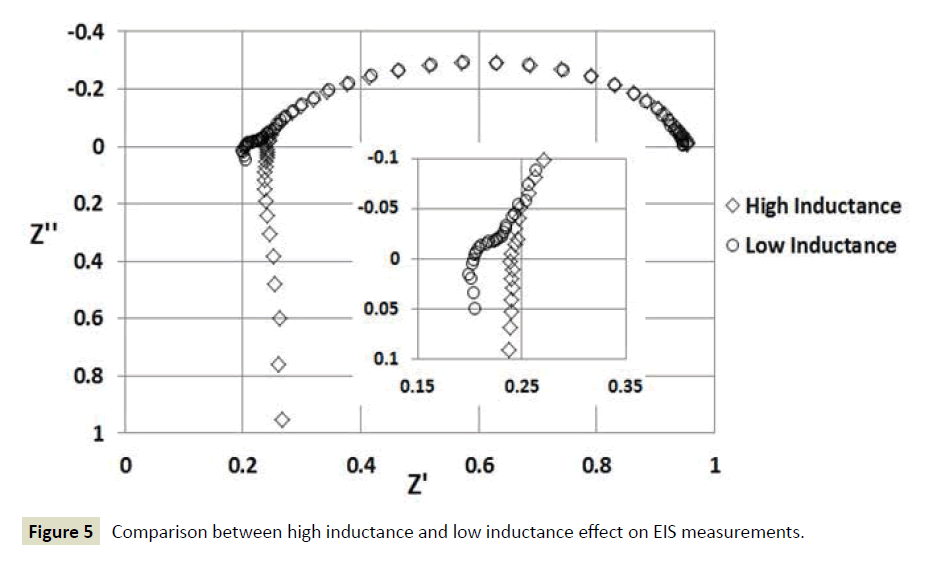
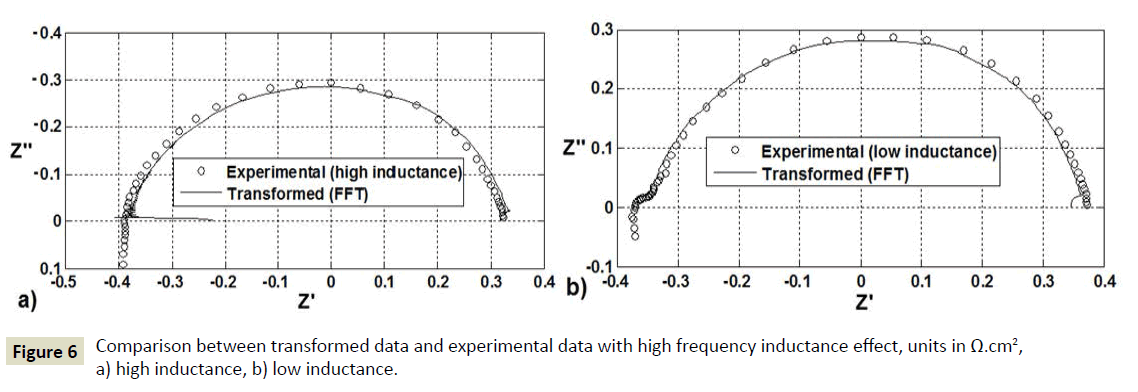
In the authors’ previous study [9] it was demonstrated that the inductance of the electrical cables of the measurement system deforms the high frequency response represented in the Nyquist plot and leads to an incorrect interpretation of the electrochemical mechanisms represented at high frequencies. In this study the FFT computational algorithm is applied to EIS measurements of a 25 cm2 H2/air PEFC with positive imaginary components at high frequencies (inductance effect from the measurement electrical cables). A FRA (Z#106 WonATech Co) connected with a RBL488 Dynaload load allowed the impedance measurements. EIS measurements were carried out at 0.2 A/cm2 and at frequencies from 10 kHz to 0.2 Hz using two different electrical cables, a conventional electrical cable (power flexible cable) and a special electrical cable (low inductive cable with fusion lug technology, TDI POWER) connected between the PEFC and the RBL488 load. The operational temperature was 50°C and the back gas pressure was held to 0.9 bar(g) for both anode and cathode. Flow rates were constant during all the experiments, hydrogen in the anode with a stoichiometry of 2.5 and air in the cathode with a stoichiometry of 3. The PEFC was operated with 100% hydrogen relative humidity (RH) in the anode; the air supplied in the cathode was dry. Figure 5 shows that the magnitude of the inductive effect of the cables is higher when using the conventional cable than using the low inductive cable. The ohmic resistance of the PEFC is commonly calculated where the imaginary component crosses the real axis at high frequencies [10-12]. Figure 5 shows that this common practice of calculating the ohmic resistance is incorrect for EIS data with high inductance effect at high frequency. This has also been demonstrated in the authors’ previous study [7]. Figure 6a shows that it is not possible to obtain a correct data transformation at high frequencies where the inductive effect is high. The real and imaginary components in a causal system such as the PEFC are even and odd functions respectively [2]. Figure 6b shows that by reducing the inductance effect of the cables it is possible to obtain a correct data transformation which can lead to a correct interpretation of the PEFC impedance spectrum in the high frequency range.
Figure 5 Comparison between high inductance and low inductance effect on EIS measurements.
Figure 6 Comparison between transformed data and experimental data with high frequency inductance effect, units in Ω.cm2, a) high inductance, b) low inductance.
Analysis of amplitude effect on EIS measurements of PEFCs
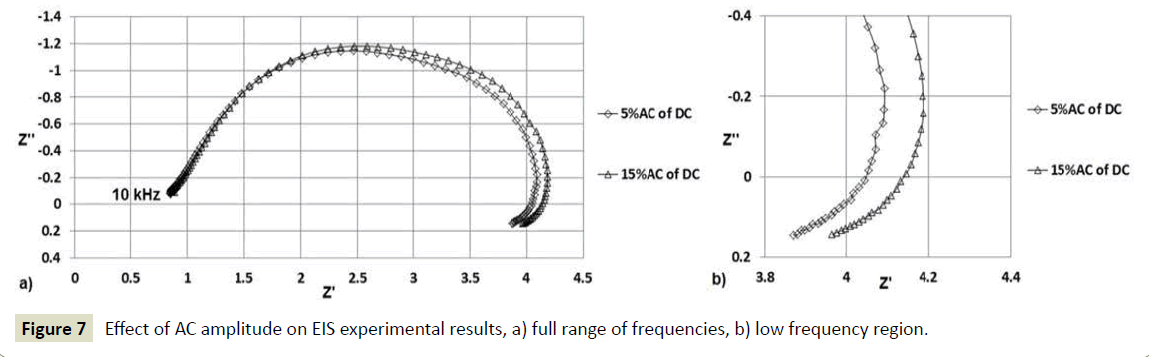
In the work reported by Xiaozi [13], AC amplitudes for 5%, 10% and 15% values of the DC current in a 500 W PEFC stack were tested. The results at 50 Amps DC current showed a small expansion of the impedance spectra at low frequencies when the AC amplitudes were increased. Overall some works [14,15] have reported that a 5% AC amplitude of the DC current is a reasonable choice but a compelling justification for this case has not yet been reported. In this study, EIS measurements were carried out with two different AC amplitudes in a 16 cm2 open cathode 4-cell PEFC stack operated at 5 Amps (0.3125 A/cm2). The PEFC stack was operated at ambient temperature 22°C and the hydrogen back pressure was held at 0.4 bar(g). The frequency scan for EIS was carried out from 10 kHz to 0.1 Hz. The amplitudes selected were 5% and 15% of the DC current (5 Amps).
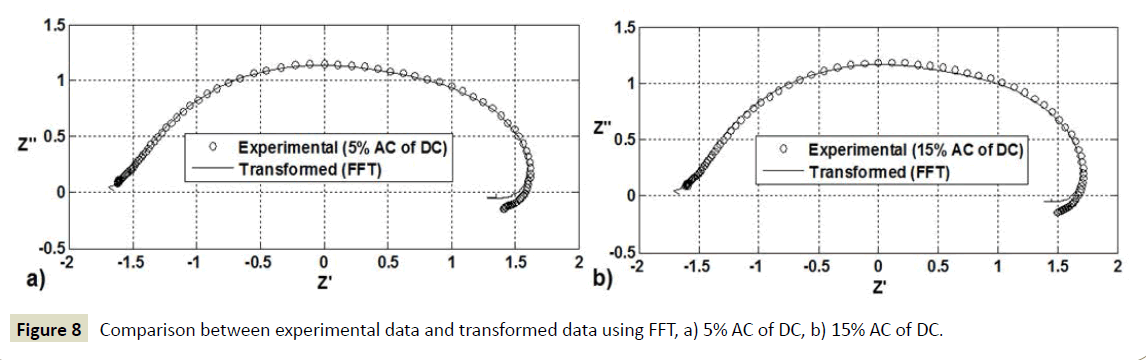
At high frequencies there is no inductive effect from the electrical cables (EIS measurements with positive imaginary components), as shown in Figure 7a. The sensing cables from the FRA to carry out EIS measurements where connected directly to the bipolar plates. The 45°C line at high frequencies is noticeable and relates to the ionic resistance in the catalyst layer (CL) [7,16,17]. At low frequency, Figure 7b, there is an expansion in the spectrum when the AC amplitude is increased. This behaviour at low frequency is consistent with the work reported by Xiaozi [11]. In this study the FFT computational algorithm is applied to EIS measurements with the two different amplitude perturbations as shown in Figures 8a and 8b. It is not possible to obtain a correct data transformation at the lowest frequencies where the EIS data resulted in imaginary Z’’ positive components. Similar to the inductance effect of the electrical cables at high frequencies shown in Figure 5, it seems that EIS measurements with positive imaginary components (inductive loop) at the lowest frequencies do not comply with the causality property for a correct data transformation Z’→Z’’, Z’’→Z’. However, this inductive loop at low frequencies has been reported as a physical process of PEFCs. Some works [18-20] have considered that the inductive loop at low frequencies can be a result of adsorbed intermediate species during the ORR. The causality property implies that the real and imaginary components in EIS measurements are even and odd functions of frequency respectively. Impedance measurements evaluated at negative frequencies would result in their complex conjugates such that.  Figures 8a and 8b demonstrate that the causality property evaluated through the FFT algorithm is not consistent for EIS measurements with positive imaginary components at low frequencies. Roy and Orazem [21] concluded that there is a K-K consistency (linearity, causality and stability) for low frequency inductive loops in the entire range (current density) of operation of the fuel cell. It is well known that the application of K-K theory with experimental data is a complicated process and has commonly been neglected in the EIS area. Even though the FFT numerical method developed in this study cannot evaluate data with positive imaginary components at low frequencies it can reliably be applied to evaluate data with negative imaginary components over the entire range of frequencies. The evaluation of data with positive imaginary components at low frequencies using the FFT computational algorithm will be investigated in future work. The effect of the amplitude on EIS measurements can be noticeable in Figures 7a and 7b. The PEFC demonstrates nonlinear current-voltage behaviour, as the current has an exponential dependence on potential. For systems presenting a nonlinear current-voltage relationship, small amplitude is needed for EIS measurements. For systems presenting a linear currentvoltage relationship very large amplitude can be used. It can be confirmed that a correct data transformation and thus valid impedance data are achieved when 5% AC amplitude of the DC current is selected in EIS measurements, as shown in Figure 8a.
Figures 8a and 8b demonstrate that the causality property evaluated through the FFT algorithm is not consistent for EIS measurements with positive imaginary components at low frequencies. Roy and Orazem [21] concluded that there is a K-K consistency (linearity, causality and stability) for low frequency inductive loops in the entire range (current density) of operation of the fuel cell. It is well known that the application of K-K theory with experimental data is a complicated process and has commonly been neglected in the EIS area. Even though the FFT numerical method developed in this study cannot evaluate data with positive imaginary components at low frequencies it can reliably be applied to evaluate data with negative imaginary components over the entire range of frequencies. The evaluation of data with positive imaginary components at low frequencies using the FFT computational algorithm will be investigated in future work. The effect of the amplitude on EIS measurements can be noticeable in Figures 7a and 7b. The PEFC demonstrates nonlinear current-voltage behaviour, as the current has an exponential dependence on potential. For systems presenting a nonlinear current-voltage relationship, small amplitude is needed for EIS measurements. For systems presenting a linear currentvoltage relationship very large amplitude can be used. It can be confirmed that a correct data transformation and thus valid impedance data are achieved when 5% AC amplitude of the DC current is selected in EIS measurements, as shown in Figure 8a.
Figure 7 Effect of AC amplitude on EIS experimental results, a) full range of frequencies, b) low frequency region.
Figure 8 Comparison between experimental data and transformed data using FFT, a) 5% AC of DC, b) 15% AC of DC.
Analysis of instability effect on EIS measurements of PEFCs
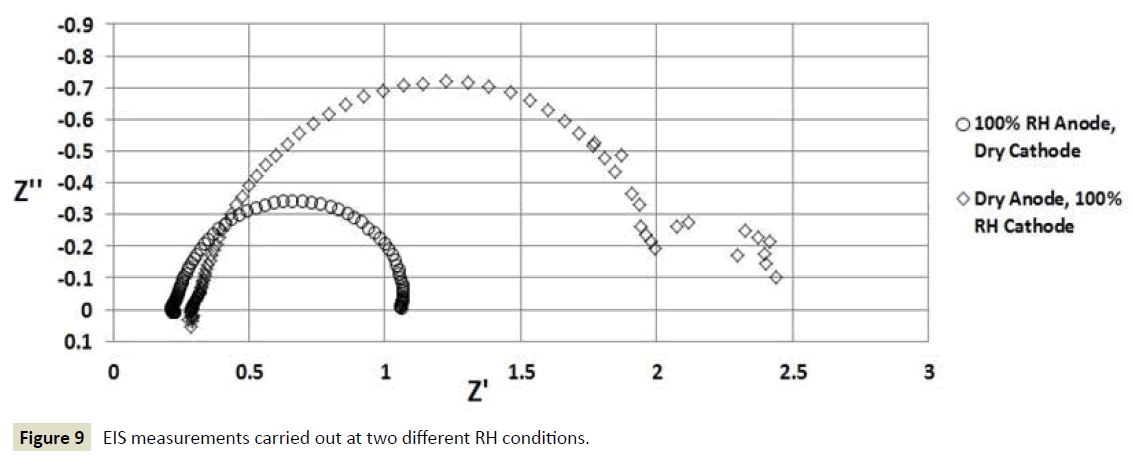
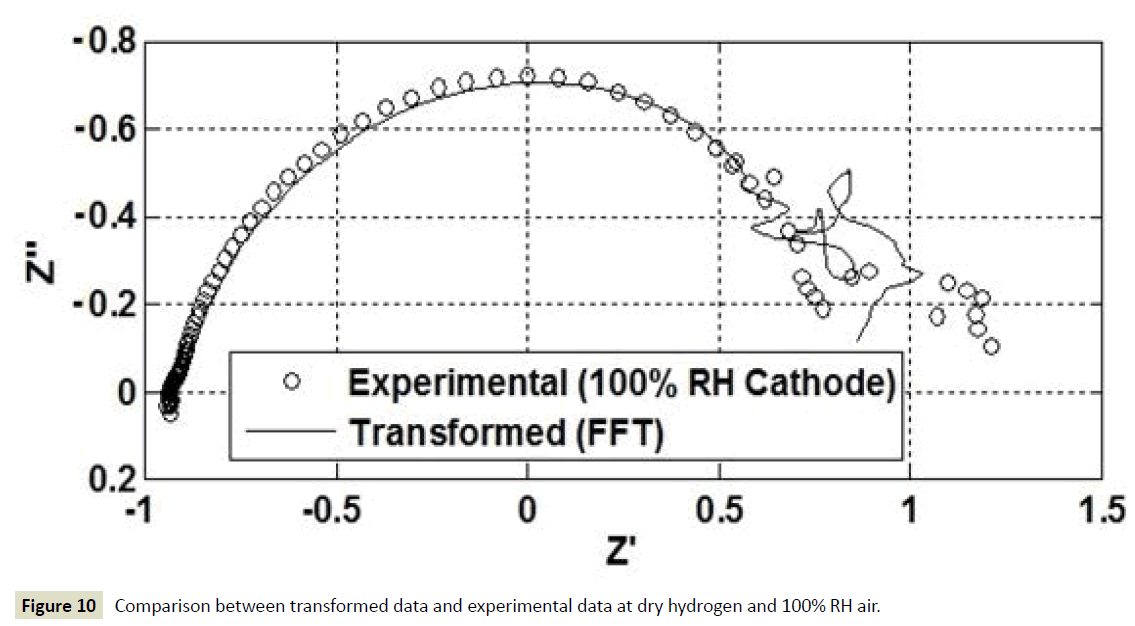
External gas humidification is desirable to ensure apposite humidification of the ionomer in the CL and the PEM. A high relative humidity (RH) enhances the ionic conductivity in the PEM and improves catalyst utilization and overall performance. Nevertheless, a high RH can result in pore saturation in the GDL and CL which will impede reactant transport. A 25 cm2 H2/ air PEFC was first operated at 0.15 A/cm2 with 100% RH in the cathode, the hydrogen supplied in the anode was dry. Secondly the PEFC was operated at 0.23 A/cm2 with 100% RH in the anode and the air supplied in the cathode was dry. Noting that the 100% RH anode/dry cathode condition was already discussed in section 4.3 where operating temperature was 50°C. EIS measurements were carried from 10 kHz to 0.1 Hz for both 100/0% anodecathode and 0/100% anode-cathode RH cases, as shown in Figure 9. There is a difference in Ohmic resistance (where the imaginary part Z’’ is zero at high frequencies) between both experimental cases. When the PEFC is operated with dry hydrogen in anode and 100% RH in air supplied to cathode, the ohmic resistance is higher than the case for 100% RH in anode and dry cathode. This increase in ohmic resistance could be attributed to dehydration in the polymer electrolyte membrane (PEM) from the anode side and from electro osmotic drag from anode to cathode. Mass transport effect is commonly represented at low frequencies in the Nyquist plot. Therefore it is expected that a difference will be observed between EIS results at different RH conditions and current densities. The decrease in diameter in the 100% RH anode-dry cathode condition is attributed to an increase in the driving force for the interfacial oxygen reduction process with increasing current density. The FFT computational algorithm was applied to EIS measurements for both RH conditions to evaluate the stability condition for correct data transformation Z’→Z’’, Z’’→Z’. The results show that the data transformation fails for EIS measurements carried out when fully saturated air and dry hydrogen are supplied in the cathode and the anode respectively, as shown in Figure 10. This failure in data transformation which leads to invalid experimental data can be a result of instability in the PEFC during EIS measurements. Therefore, the frequency response of the PEFC under such conditions is not time invariant. Water in a PEFC is produced in the cathode side due to the ORR, so when air is supplied with a high RH an increase in water concentration in the cathode is present. Within the fuel cell there is a competition mainly between back-transport of water from cathode to anode and electro-osmotic drag of water by ions from anode to cathode which could lead to instability during PEFC operation.
Figure 9 EIS measurements carried out at two different RH conditions.
Figure 10 Comparison between transformed data and experimental data at dry hydrogen and 100% RH air.
The FFT computational algorithm was also applied to EIS measurements carried out when the anode was at 100% RH and dry air was supplied to the cathode and was demonstrated in section 4.3 as shown in Figure 4. Yan et al. [22] reported that optimal performance in a PEFC can occur at low air relative humidity and high hydrogen relative humidity. Figure 4 shows that the frequency response of the PEFC under such operating conditions is time invariant and complies with the stability properties for correct Z’→Z’’, Z’’→Z’ data transformation.
Comparison between FFT algorithm and K-K analysis from Zview software for impedance data evaluation
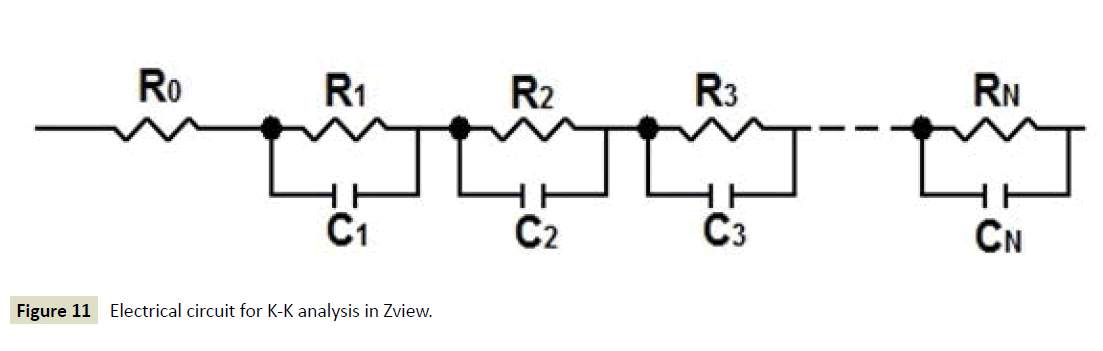
Boukamp [23] reported that it is possible to evaluate K-K relations by fitting the Voigt R-C model (R-C circuits in series) into EIS measurements. Boukamp also reported that if the EIS data cannot be well approximated by the Voigt model containing a reasonable number of R-C pairs, it means that data are not transformable and do not represent the physical processes of the electrochemical system studied. The Voigt R-C model as shown in Figure 11 was constructed in Zview to carry out a K-K analysis of EIS measurements. To carry out K-K analysis using Zview, first the circuit shown in Figure 11 has to be fitted to EIS measurements, thereafter the K-K mode is selected in the Setup option in Zview.
Figure 11 Electrical circuit for K-K analysis in Zview.
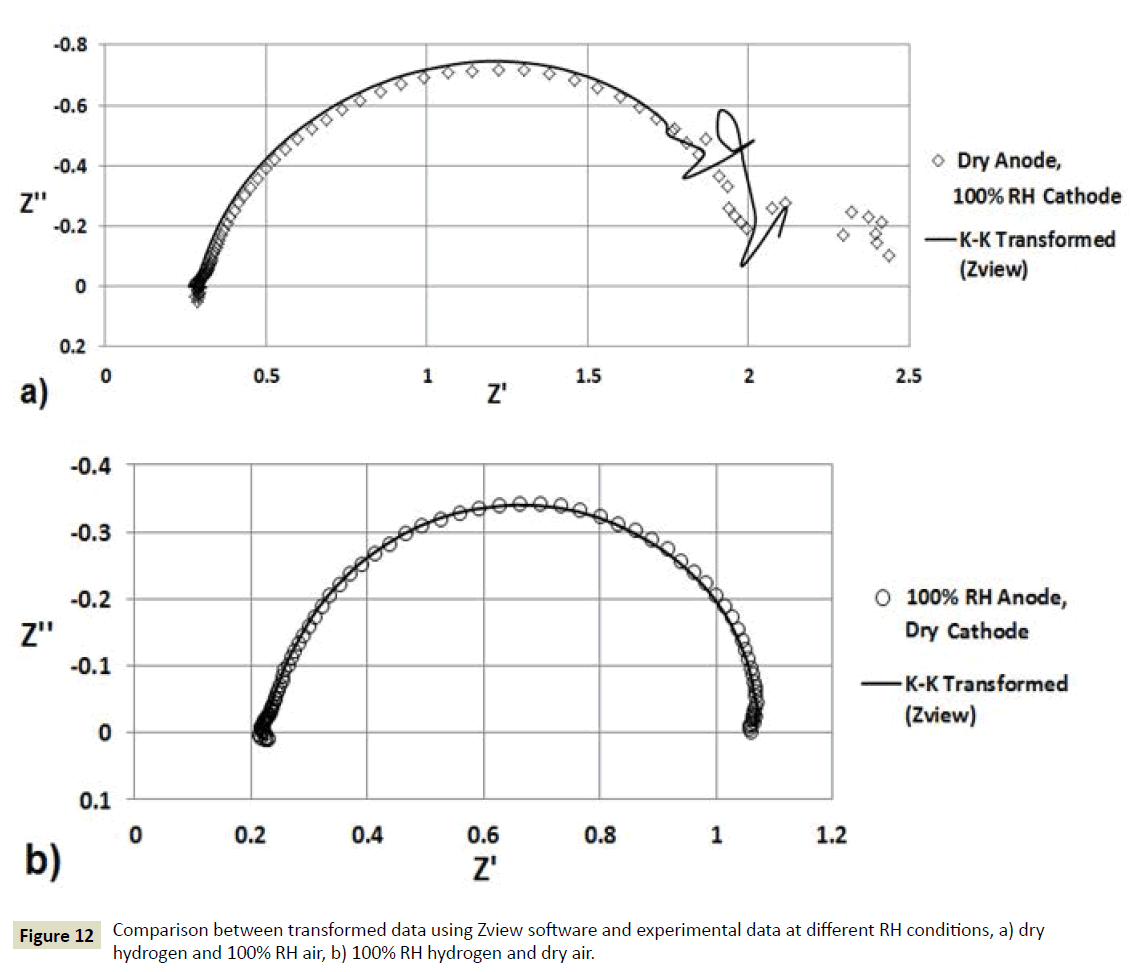
EIS measurements shown in Figure 9 for a PEFC during two different RH conditions were considered to evaluate the measurements through K-K in Zview software. The electrical circuit shown in Figure 11 was applied to the EIS measurements by constructing and fitting one R-C pair at a time in Zview. The EIS measurements for dry anode-100% RH cathode condition were evaluated at first. There was no difference on the fitted data, after constructing six R-C pairs. After that the K-K analysis was carried out and this resulted in the K-K transformation shown in Figure 12a. The same procedure was carried out for the measurements for 100% RH anode-dry cathode condition. Four R-C pairs were required and the resulting K-K analysis is shown in Figure 12b. The results shown in Figures 12a and 12b using Zview software are in agreement with the results shown in Figures 4 and 10 using the Matlab script based on FFT. Similar to the results shown in Figure 10, it was not possible to obtain data transformation in the measurements resulted from the 100% RH cathode condition using K-K in Zview. Although Zview software is a good tool to carry out K-K evaluation, the method is not straightforward as the procedure requires knowledge and use of electrical circuits that comply with K-K theory. The computational script developed in this study could be applied to evaluate correctness of EIS measurements of PEFCs without expensive software and lowcost FRAs [9].
Figure 12 Comparison between transformed data using Zview software and experimental data at different RH conditions, a) dry hydrogen and 100% RH air, b) 100% RH hydrogen and dry air.
Conclusions
The validity of EIS measurements in an electrochemical system is commonly evaluated by calculating the imaginary component from the real component and viceversa. However, this evaluation in EIS measurements of fuel cells is commonly neglected in the industrial and academic fuel cell area due to the complexity of the method to be applied to real-world impedance measurements. This evaluation is very important in order to correctly interpret the electrochemical mechanisms of PEFCs represented in the Nyquist plot. A correct data transformation Z’→Z’’, Z’’→Z’ implies that EIS measurements are carried out in an electrochemical system under linear, steady and causal conditions and truly represent the mechanisms of the electrochemical system studied. This study has demonstrated that the most common factors that lead to invalid EIS data in PEFCs can be identified using the FFT computational algorithm. The FFT numerical method was developed and applied to EIS measurements carried out in a single PEFC and stack PEFC to evaluate correctness in the measured data. The results showed that inductance of the electrical cables of the measurement system, large amplitude AC signal superimposed onto the bias current or potential and instability of the PEFCs lead to invalid EIS measurements. EIS measurements with positive imaginary components at low frequencies (inductive loops) have been reported to represent a physical process occurring inside the PEFC. The FFT computational algorithm cannot evaluate data transformation in such low frequency measurements. Future work will investigate how to correctly evaluate inductive loops at low frequencies in PEFCs using this FFT computational algorithm. The method developed in this study can ensure correctness in EIS data to enable the study of the performance and state of health of fuel cells.
Appendix
Computational algorithm to evaluate EIS data using FFT in Matlab
Note: the algorithm steps shown below have to be run in a single script in Matlab
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%
%Experimental data to evaluate
%Imaginary component of experimental data (expressed without complex term i)
img=[-0.00049 -0.00614775 -0.01115025 …-0.0049615]
%Real component of experimental data
re=[0.271125 0.27435 0.261675 … 1.442375]
%Experimental frequency tested
freq=[20000 15887 12619 … 0.1]
%Calculate the new frequency range as expressed in Equation 4
minim=find(img==min(min(img)))
delta=2.*atan(frEquation/freq(minim))';
a=linspace(0,pi,1024);
%Imaginary to real transformation Z’’→Z’
%Step 1 Interpolated imaginary component at negative and positive frequencies
b= interp1(delta,img,a)';
c = -b ;
d = c(end:-1:1);
e=cat(1,b,d);
e(isnan(e))=0;
%Step 2 FFT is applied to the imaginary interpolated data
f=fft(e);
%Step 3 The resulting data at positive frequencies are set to be zero.
f(2:1025)=0;
%Step 4 The data at negative frequencies resulting from step 2 are conjugated, doubled and concatenated with data from step 3
g = conj(f(1026:2048)) ;
k=cat(1,2.*f,g);
%Step 5 The inverse FFT is applied and the transformed real components at positive frequencies are calculated
m=ifft(i.*k,2048);
Re_trans=m(1:1024);Q
%Real to imaginary transformation Z’→Z’’
%Step 1 Interpolated real component at negative and positive frequencies
b_real= interp1(delta,re,a)';
c_real = -b_real ;
d_real = b_real(end:-1:1);
e_real=cat(1,b_real,d_real);
e_real(1024)=e_real(1);
e_real(1025)=e_real(1);
e_real(isnan(e_real))=[];
%Step 2 FFT is applied to the real interpolated data
f_img=fft(e_real);
%Step 3 Data at negative frequencies are set to be zero
f_img((size(e_real)/2)+1:size(e_real))=0;
%Step 4 The data at positive frequencies resulting from step 2 are conjugated, doubled and concatenated with data from step 3
g_img = conj(f_img(1:size(e_real)/1)) ;
h_img = g_img(end:-1:1);
k_img=cat(1,2.*f_img,h_img);
%Step 5 The inverse FFT is applied and the transformed imaginary components at positive frequencies are calculated
m_img=ifft(i.*k_img,2048);
rE_img=(-m_img);
Img_trans=rE_img(1:1024);
%%%%%%%%%%%%%%%%%%%
%Plotting results
%Experimental data
%The real components Z’ of the experimental data are shifted to be zero where the imaginary %component Z’’ reaches its minimum value
plot((realv-realv(minim)),imagina,'b')
xlabel('Real');
ylabel('Imaginary');
hold on
% Transformed data
%Only positive frequencies
plot(Re_trans(1:1024), Img_trans(1:1024),'r')
xlabel('Real');
ylabel('Imaginary');
grid;
hleg1 = legend('Experimental','FFT transformed');
References
- Urquidi-Macdonald M, Real S, Macdonald DD (1986) Application of Kramers?Kronig Transforms in the Analysis of Electrochemical Impedance Data II. Transformations in the Complex Plane. J Electrochem Soc 133: 2018-2024.
- Orazem ME, Tribollet B(2008) Electrochemical Impedance Spectroscopy, Wiley, New Jersey, USA.
- VanderNoot TJ (1992) Hilbert transformation of immittance data using the Fast Fourier Transform. J Electroanal Chem 322: 9-24.
- Cruz-ManzoS, Chen R (2013)A generic electrical circuit for performance analysis of the fuel cell cathode catalyst layer through electrochemical impedance spectroscopy. J ElectroanalChem 694: 45-55.
- Mathworks.com (2015) Share the work you do in MATLAB with others Mathworks.com. Accessed on: 21 August 2015.
- Meyer Q, Barass S, Curnick O, Reisch T (2013) A multichannel frequency response analyser for impedance spectroscopy on power sources. J Electrochem Sci Eng 3: 107-114.
- Fouquet N, Doulet C, Nouillant C, Dauphin-Tanguy G, Ould-Bouamama B, et al. (2006) Model based PEM fuel cell state-of-health monitoring via ac impedance measurements. J Power Sources 159: 905-913.
- Papoulis A (1962)The Fourier Integral and its Applications, McGraw-Hill, New York, USA.
- Cruz-Manzo S, Chen R, Rama P (2012)Inductive Effect on the Fuel Cell Cathode Impedance Spectrum at High Frequencies. J Fuel Cell Science Technology 9: 051002.
- Ciureanu M, Roberge R (2001)Electrochemical Impedance Study of PEM Fuel Cells. Experimental Diagnostics and Modeling of Air Cathodes. J Phys Chem B 105: 3531-3539.
- Liu F, Yi B, Xing D, Yu J,Hou Z,et al. (2003)Development of novel self-humidifying composite membranes for fuel cells. Power Sources 124: 81-89.
- Li G, Pickup PG (2003) Ionic Conductivity of PEMFC Electrodes. JElectrochem Soc 150: C745–C752.
- Yuan X, Sun JC, Wang H, Zhang J (2006) AC impedance diagnosis of a 500 W PEM fuel cell stack: Part II: Individual cell impedance. J Power Sources 161: 929-937.
- Gode P, Jaouen F, Lindbergh G, LundbladA, Sundholm G, et al. (2003) Influence of the composition on the structure and electrochemical characteristics of the PEFC cathode. Electrochim Acta 48: 4175-4187.
- Jaouen F, Lindbergh G,Wiezell K (2003) Transient Techniques for Investigating Mass-Transport Limitations in Gas Diffusion Electrodes II. Experimental Characterization of the PEFC Cathode. J Electrochem Soc 150: A1711-A1717.
- Lefebvre MC, Martin RB,Pickup PG (1999)Characterization of Ionic Conductivity Profiles within Proton Exchange Membrane Fuel Cell Gas Diffusion Electrodes by Impedance Spectroscopy. ElectrochemSolid-State Lett 2: 259-261.
- Gazzarri J,Eikerling M, Wang Q, Liu Z (2010) Estimation of Local Relative Humidity in Cathode Catalyst Layers of PEFC. Electrochem Solid-State Lett 13:B58-B62.
- Makharia R, Mathias MF, Baker DR (2005)Measurement of Catalyst Layer Electrolyte Resistance in PEFCs Using Electrochemical Impedance Spectroscopy. J Electrochem Soc152: A970-A977.
- Xie J, Wood III DL, More KL, Atanassov P, Borup RL, et al.(2005) MicrostructuralChanges of MembraneElectrodeAssembliesduring PEFC DurabilityTesting at High HumidityConditions. J Electrochem Soc 152: A1011-A1020.
- Inaba M, Yamada H, Tokunaga J, TasakaA (2004) Electrochem. Effect of Agglomeration of Pt/C CatalystonHydrogenPeroxideFormation. ElectrochemSolid-State Lett 7: A474-A476.
- Roy SK, Orazem ME (2007) Interpretation of Low-Frequency Inductive Loops in PEM Fuel Cells. JElectrochemSoc154:B1378-B1388.
- Yan Q, Toghiani H, Causey HJ (2006) Steady state and dynamic performance of proton exchange membrane fuel cells (PEMFCs) under various operating conditions and load changes. Power Sources 161: 492-502.
- Boukamp BA(1995) A Linear Kronig?Kramers Transform Test for Immittance Data Validation. J Electrochem Soc 142: 1885-1894.



 where b is the Tafel slope, ηS represents a value of voltage in activation over potential, and j0 is the exchange current;
where b is the Tafel slope, ηS represents a value of voltage in activation over potential, and j0 is the exchange current;  is defined as the Warburg impedance and describes diffusion across a finite dimension in the frequency domain [
is defined as the Warburg impedance and describes diffusion across a finite dimension in the frequency domain [ defined as resistance for the diffusion process and
defined as resistance for the diffusion process and  D defined as the time constant to diffuse oxygen through the CCL; Y represents a parameter related to capacitance, superscript P represents a parameter to correct the inhomogeneity in the distribution of charge between the electrode-electrolyte inteface; ω is the angular frequency; i is the imaginary component in impedance; Re represents the total ohmic resistance to flow of electrons and ions in the bipolar plate, gas diffusion layer (GDL) and polymer electrolyte membrane (PEM); x represents the thickness of the CCL (dimensionless) and for EIS measurements is equal to 1. Equation 1 was fitted to the EIS measurements of a 25 cm2 H2/air PEFC operated at 0.12 A/cm2 and the resulting parameters are shown in Table 1.
D defined as the time constant to diffuse oxygen through the CCL; Y represents a parameter related to capacitance, superscript P represents a parameter to correct the inhomogeneity in the distribution of charge between the electrode-electrolyte inteface; ω is the angular frequency; i is the imaginary component in impedance; Re represents the total ohmic resistance to flow of electrons and ions in the bipolar plate, gas diffusion layer (GDL) and polymer electrolyte membrane (PEM); x represents the thickness of the CCL (dimensionless) and for EIS measurements is equal to 1. Equation 1 was fitted to the EIS measurements of a 25 cm2 H2/air PEFC operated at 0.12 A/cm2 and the resulting parameters are shown in Table 1.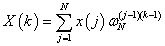 (2)
(2)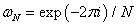
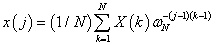
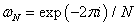 (3)
(3)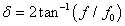 (4)
(4) ,
,  . The following procedure is developed in a script in Matlab® (see Appendix) to calculate the real components from imaginary components (Z’’→Z’ transformation).
. The following procedure is developed in a script in Matlab® (see Appendix) to calculate the real components from imaginary components (Z’’→Z’ transformation).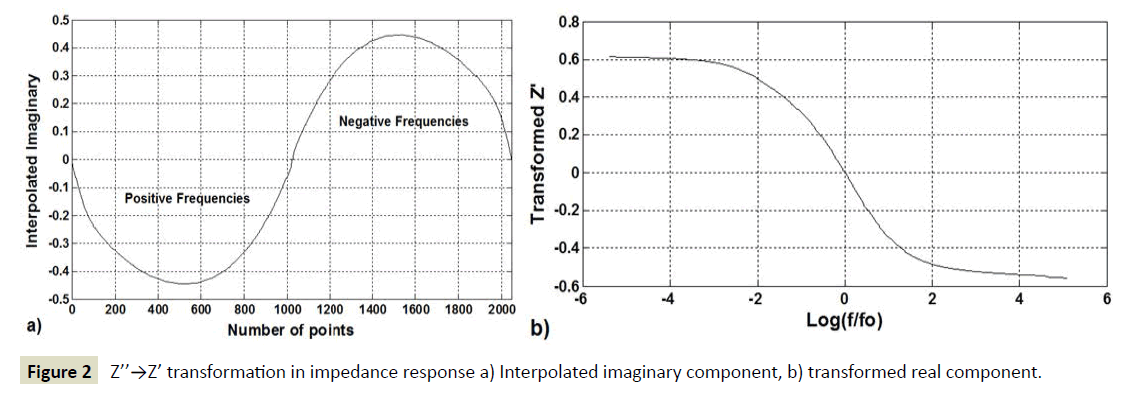
 Figures 8a and 8b demonstrate that the causality property evaluated through the FFT algorithm is not consistent for EIS measurements with positive imaginary components at low frequencies. Roy and Orazem [
Figures 8a and 8b demonstrate that the causality property evaluated through the FFT algorithm is not consistent for EIS measurements with positive imaginary components at low frequencies. Roy and Orazem [