Research Article - (2012) Volume 2, Issue 5
1Islamic azad University, Qazvin branch
2Malek-e-Ashtar University of Technology, Tehran
3AmirKabir University of Technology, Tehran
4Shahid Sattari Aeronautical University of Science and Technology, Tehran
In the present research, laboratory shock tube of the Amirkabir University of Technology (AUT) is determined for practical and CFD simulation investigation for moving normal shock wave. The shock tube is geometrically simple and totally axisymmetric. Pressurized gas is produced by a piston compressor stored in a high pressure tank. There are two study cases with the different driver gas pressure and diaphragm thickness. Both driver and driven gas is air. The driven gas part is open to atmosphere. Diaphragms are made of aluminium foil blasting in a certain pressure. There are two pressure sensors in order to capture the moving normal shock wave time intervals. Therefore the speed of moving shock wave is definable. Both cases are considered for CFD simulations. Simulations are done in transient form for laminar viscose flow regime in 2D, axisymmetric geometry. the walls considered to be adiabatic. The time step for simulation is 1e-05 sec which make the case convergent in 20 iterations. The time intervals are very short so the assumptions of adiabatic walls and laminar flow are trustworthy. Map quadrilateral grid employed for domain descritization, so the moving normal shock wave can be captured very well. grid independency study is done for both cases. However the effects of boundary layer and shockwave interaction and wall shear stress are not the goal of present study, but the boundary layer mesh is generated near wall for further studies. Time intervals data for passing shock wave from simulations and engineering calculations show good compatibility with practical data.
Shock tube-Transient flow simulation-Normal shock wave-CFD
Nowadays the usage of Computation Fluid Dynamics in high speed aerodynamics is dramatically increased in aerodynamic facilities design process. There are many different ways to generate a source of air at a sufficiently speed and pressure to act as the working fluid of a hypersonic wind tunnel. This includes hotshot tunnels, plasma jets, shock tubes, shock tunnels, free-piston tunnels, and light gas guns. Various hypersonic wind tunnels have been constructed at different universities and research centers all over the world. However, these facilities are very costly and very expensive to run and maintain, the shock tubes are very simple and reasonably low cost to build and operate. The shock tube is a high speed aerodynamic test facility that enables investigation of moving shock wave and the loads imposed over a model for high speed flow regimes. To have a pre-view of the flow and moving shock wave through a shock tube before starting the design process, using the CFD is the best way. Shock tube in its simplest form is a tube with fixed cross section that is divided by a diaphragm into two areas. After the diaphragm ruptured, a shock wave proceeds in low pressure area and expansion waves proceed into high pressure area. The conventional process of a normal shock wave traveling and wave diagrams in a simple shock tube are shown in Figure 1. In the present study, the goal is to capture the moving shock wave and the distribution of aerothermodynamics properties on the wall of tube. Reflected shock wave is not investigated here. There are many practical investigations on shock tube but numerical simulations are not too many. Daru and Tenaud made a numerical simulation study on reflected shock wave and laminar boundary layer interaction in a shock tube and defined proper grid congestion for such a case. They have shown that 4.5 million nodes are sufficient and reliable for such a case [1]. Al-Falahi et al. developed two dimensional time accurate Euler solver for shock tube applications. In this study, uniform grid spacing with the number of 356 is used and good results in comparison with practical data were obtained [2]. All mentioned studies make a good view into flow in shock tubes, but making a fast accurate method for laminar, ax symmetric flow analysis is not available. In present study, a shock tube can be simulated in a CFD code very fast and reliable.
Figure 1: Wave diagrams in a simple shock tube
A very important item in numerical simulation of a shock tube is to use proper grid congestion for capturing the thin layer of moving shock wave. It is also important to generate quadrilateral cells in map form and perpendicular to the flow direction.
Specifications of test facility
The test facility includes a piston compressor, a pressurized tank, a simple shock tube and three sensors that two of them are fast response type. the first sensor measures the pressure of behind of the diaphragm and two fast response sensors duty is to capture the moving shock wave passage. The constant internal diameter of the stainless steel tube is 67 mm and the total length of tube is 2080 mm and the diaphragm is installed in the 640 mm from the head. The fast response sensors are located in 15.5 cm and 115.5 cm respectively after diaphragm. There are two sets of tests and in both the driver gas is dry air. The diaphragms are made of Aluminum foil with the thicknesses of 50 and 80 μm which destruct in 2.7 and 4.8 bar gauge pressure respectively for case1 and 2. Atmospheric conditions are important for tests, because the low pressure part of shock tube is open to atmosphere and speed of shock wave is a function of pressure ratio of back and front of diaphragm. The instruction of test facility is shown in Figure 2. It is important to have the atmospheric condition when running each test. The atmospheric conditions are tracked and presented in table 1.
Figure 2: Geometry of shock tube of the AUT
Table 1: Initial conditions for simulations
Numerical simulation methods
For present research, the conventional Navier Stokes equations in axisymmetric form employed for compressible gas simulations. Supplementary data are available in reference [3]. The operating fluid considered to be air as a perfect gas with the vary Cp and thermal conductivity as function of temperature and constant molecular weight. Viscosity is a function of temperature and modeled by Sutherland's law. Simulations are done in transient mode with the time step of 1e-05 sec. The pressure-base solver with the Simple mode for pressure-velocity coupling employed and discretizations for pressure, density, momentum and energy are done in second order.
The assumption of laminar regime is physically true in shock tubes where the duration of test and the Reynolds number are very low. The initial conditions are the pressure, velocity and temperature for both sides of diaphragm which is shown in table 1. In this table P is static pressure, V is velocity and T is temperature. Governing equations consist of conventional continuity, momentum and energy for laminar, adiabatic, axisymmetric flow. For 2D axisymmetric geometries, the continuity equation can be written as Eq. (1),
Where x is the axial co-ordinate, r is the radial co-ordinate, vx is the axial velocity, vr is the radial velocity andr is density. For a 2D axisymmetric flow, the axial and radial momentum conservation equations can be written as Eq. (2) and Eq. (3), respectively.
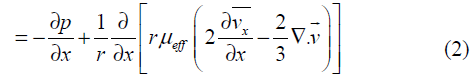
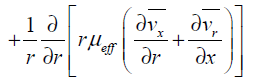
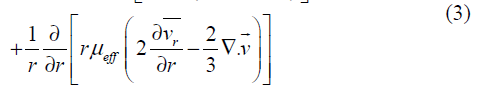
where
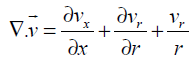(4)
In general form, the energy conservation concept can be formulated as Eq. (5),
Where,
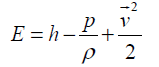(6)
For compressible flows, the equation of state (considering ideal-gas concept) can be written as Eq. (7) where R is the universal gas constant and T is the static temperature.
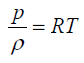
Grid generation
The domain of simulation is very simple and consists of a tube. Because of the axisymmetric shape of tube, only half of the model is needed for simulation. Structured quadrilateral grid type is employed for throughout the domain and the boundary layer grid is generated near wall, so there are 228000 cells in domain. A portion of grid in domain is shown in Figure 3. To study the grid-independency, two other cases considered for simulation with 900000 cells and results show no significant variation.
Figure 3: Grid congestion near wall
The practical data extracted from two sensors after the diaphragm only show the time intervals of passing shock. By using the conventional relations and analytical formulas for shock tubes [4] for 2D, adiabatic and inviscid flow, the velocity of moving shock is definable from ratio of driver gas to driven gas pressure. Table 2 shows the results from practical tests, simulations and analytical calculations and the results are matched very well. In table 2, t is time interval for shock to move from sensor 2 location to sensor 3. The data show that the analytical formulas for semi 2D are reliable in constant area circular shock tube.
Table 2: simulation and experimental results
Figure 4 and 5 show the distribution of static pressure along the axis of tube for case1 and 2 for two time intervals. In case2, pressure ratio in start is higher rather than case1 and the peaks of pressure in shock position is more than case1 which shows that the shock in case1 is more powerful than case1, also the speed of shock in case2 is more than case1 as predicted before. As it is shown in Figure 4 and 5, power of the shock waves in time intervals for each case remains semi-fixed. Figure 6 shows contour of velocity for case1 and 2 when the shock wave is positioned in the sensor 3 location. It shows that in both cases for specified time, the expansion waves are not reached to the left wall yet, but it is obvious that in the same shock position, the left wall of tube experiences more pressure drop in case1. Figures 7 and 8 show the contour of static pressure in three time intervals for case 1 and 2 respectively. The position of normal shocks and pressure distribution can be tracked. Figure 9 shows the distribution of static temperature in t=2 msec. As mentioned before, the shock wave in case 2 is more powerful rather than in case 1. The shock wave in case1 moves faster to the right but the expansion waves are slower move to the left rather than case2. It is because of the more temperature in front of shock wave and less temperature in front of expansion waves. However the study of shock wave and boundary layer interactions are not the main goal of present study but the grid congestion is considered near wall and the Figure 9 shows the velocity vector near wall just before the normal shock wave.
Figure 4: Distribution of static pressure along axis over wall for case1
Figure 5: Distribution of static pressure along axis over wall for case2
Figure 6: Contour of velocity magnitude
Figure 7: Contour of static pressure (Pa) for case 1
Figure 8: Contour of static pressure for case 2
Figure 9: Boundary layer just before normal shock wave
Figure 10: Distribution of static temperature along axis for case1 and 2 in t=2 msec
In present research shock tube of AUT is investigated experimentally and by CFD simulations. Simulation results show good compatibility to experimental data. It is shown that the power and speed of moving shock wave increases when the pressure ratio of driver to driven gas increased. Congestion of grid is studied for capturing the shock wave however for considering the shock wave and boundary layer interactions, a denser grid must be employed. The represented method can simulate flow in a shock tube very quickly and can be used for design and manufacturing a new shock tube facility. The location of the sensors can be determined easily. In the practical tests, it is shown that for capturing the pressure of flow it is necessary to employ ultra high-response pressure transmitter sensors known as PiezoElectric otherwise the data would not be trustworthy. If the data logger and data capturing systems are located far from test facility, it is recommended to use ampere transmitters rather than voltage ones. The next step of present study is to use helium gas instead of air for driver gas to make higher Mach numbers by employing species equations and modeling shock wave and boundary layer interaction in the presence of model.
