Research Article - (2017) Volume 7, Issue 3
1Department of Mathematics, University of Wyoming, Laramie, WY, USA
2Department of Molecular Biology and School of Energy Resources, University of Wyoming, Laramie, WY, USA
Received date: March 21, 2017; Accepted date: May 30, 2017; Published date: June 15, 2017
Citation: Mueller S, Jafari F, Roth D (2017) Improving Dependability and Precision of Data Encoding in DNA. Eur Exp Biol. Vol. 7 No. 3:19. doi: 10.21767/2248-9215.100019
Copyright: © 2017 Mueller S, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
DNA storage of information is emerging as the next-generation approach to archiving vast amounts of data. Various sophisticated approaches for data storage in DNA have been proposed. Herein we present a multistep algorithm designed to detect and/or correct errors introduced at any stage of the DNA storage process, including those during message DNA generation, and propose refinements designed to ensure authenticity and correctness of each individual encoded DNA block. In addition, the algorithm allows authentic decoding without a reference sequence or message meaning. The algorithm is designed based on principles underlying provably secure cryptographic systems. Importantly, our new algorithm compares favorably with current ones in terms of ease of implementation and message expansion. In cases where reads are error-free, our algorithm should be faster than current alignment techniques. Without knowing the original data, a certificate is generated that confirms that the obtained data are exactly the same as the original. Our algorithm has applications to DNA steganography, sequence alignment, fast identification of correct reads in next generation sequencing and to message security.
Digital information storage in DNA; Error detection; Error correction; Next generation sequencing; Alignment algorithm
The potential of DNA has been realized for various information-theoretic protocols, including DNA steganography for the identification of genetically modified organisms, hiding of messages in DNA and long-term data storage in DNA. These applications require mechanisms to validate, ensure, and possibly verify message accuracy [1]. This is particularly important when correctness of the retrieved data is not variable by a reference sequence or other means such as a comparison with a meaningful text template. DNA is a typical code and so are all the information theoretic algorithms that utilize it. However, what is seen by the receiver of the message might not be the same as what was initially sent or encoded. Thus, it is critical that processes using DNA for data storage have dependable and precise error correcting or detecting features [2].
Storing messages in DNA was first demonstrated in 1988 and the largest project to date encoded about 750 kilobytes of data, including text, tables, photos, and video. As with any computer code, DNA coding approaches are susceptible to errors during construction of the code, storage, and read-out. Relative to these issues, algorithms to develop in vivo and in vitro based approaches to utilizing DNA as a framework for archiving large data sets have been developed [3].
Two of the most promising approaches for information archiving in DNA use in vitro algorithms and next-generation DNA synthesis and sequencing. Both approaches rely on the sequencing of multiple oligonucleotides (nt) per message component. In Ref. 7 they reported an average of ≈3000-fold coverage of each recovered nucleotide base. However, there were message sequences with only single coverage from amplification procedures and these contributed to process errors. The work in Goldman et al. relied on the sequencing of ≈107 copies for each DNA string. Given that the sequencing reaction consumed ≈0.1% of the DNA of the initial library, two components were not sequenced at all and had to be specifically sequenced with manual techniques. This result was suggested to be due to specific self-complementary regions that led to hybridization and sequencing failure [4]. Although both projects report a significant average coverage, neither was sufficient for complete error protection.
To address these issues Church et al. relied on multiple message copies to identify errors, and Goldman et al. [10] employed additional explicit error correcting features. However, with current approaches it is still di cult to consistently ensure appropriate coverage of every single nt that is necessary for correction of errors generated due to message mutation, especially if there is no reference for determining if the obtained reads reflect the authentic message [5]. This is, in turn, is dependent on the length and quality of continuous sequences that provide appropriate alignment of overlapping reads.
Similar error correction issues impact next generation DNA sequencing technologies. Current alignment programs developed to handle the numerous individual reads use three main approaches: (i) “hashing” the read sequences and scanning through the reference sequence: (ii) “hashing" of the reference genome and (iii) merge-sorting of the reference subsequences and read sequences.
Herein, we present a multistep algorithm that increases the reliability and precision of existing approaches without negatively impacting efficiency and effectiveness. In particular, our algorithm establishes a significant guarantee of message validity, authenticity and integrity [6]. It also can be applied for the archiving of vast data sets, in optimization of DNA sequencing algorithms, and in precisely tagging genetically modified organisms (GMOs). Our solution also specifically identifies which reads are correct prior to majority voting and prior to knowing the message meaning. Given appropriate reads this approach allows pooling of the correct sequences and facilitates rapid and accurate decoding [7].
Examples of errors in DNA storage protocols are summarized in Table 1. Analysis of the robustness of current algorithms under single sequence coverage identified significant distortions of encoded text, video, or pictures from sequence errors which may render decoding totally untranslatable [8]. The most complete algorithm to date in terms of error correction is that of Goldman et al. Analysis of identified a potential problem during assembly of the decoded sequence reads where two specific regions were not recovered from any sequenced read. Repeats of this motif had a self-reverse complementary pattern and it was hypothesized that long, selfcomplementary DNA fragments might not be readily sequenced using the Illumina process or other next generation sequencing protocols. It had previously been determined that individual sequences, especially those containing large GC content or long selfcomplementary regions are difficult to accurately read or synthesize.
| Algorithm STEPS and their Main Features | ||
|---|---|---|
| Sequence of Steps | Main Features | Comment |
| Step 1, Step 2 | Detection of substitution errors | To detect t substitution errors, choose R such that R.S 2t + 1 |
| Step 3, Step 2 | Improved randomization | The randomization function number 7 in STEP 1 may lead to self-complementary patterns, e.g., when encoding consecutive 1's. Simple cryptographic techniques yield a higher degree of randomness to prevent self-complementarity and other harmful patterns |
| Step 3, Step 4, Step 2 | Detection of any errors, including those during message DNA preparation | Authenticity is established via a cryptographic hash value that is appended to the message part before sequencing. This enables the choice of the correct reads (provided at least one exists, i.e., that S>0) |
| Step 3, Step 5, Step 2 | Proof of Authenticity of the individual segments | Similar to previous steps, but more efficient |
| Summary of potential errors in storing data in DNA with existing approaches | ||
| Type of problem | Previous approaches | Our approach |
| Efficient generation de-novo of DNA according to predetermined design | Generation of short DNA segments with small potential for errors | Same as [7,10] |
| Individual pieces require correct identification and alignment during decoding | Segmentation into both data and addressing info | Same as [7,10] |
| ID and address of individual segments needs to be included in the code | Parity check to test obtained indexing identification | Included as part of robustness features of algorithm techniques |
| Sequences with specific properties or structure cannot be sequenced | Reverse-complementation, 25 bp of set the homopolymer rule, manual correction, randomization | Refined randomization |
| Errors can occur in each individual step of the Algorithm | Coding theory and ampli cation and/or sequencing of many strings | Tools derived from provably secure crypto systems |
| Errors that occur early cannot be identified or corrected. | Manual intervention | Proof of correctness of obtained strings and Proof of completeness of recovered data via a simple cryptographic solution |
This table provides a comparison of type. of problems that can arise when using DNA as data storage, the previous approaches in dealing with these problems and our approach. In combining the strengths of the existing methods via coding theory with our proposed cryptographic solutions, the algorithm is simplified and made more efficient. The last step utilizes a specific optimal scheme from cryptography (Optimal Asymmetric Encryption Padding) which is probably the most efficient way to ensure correctness of the entire string along with adequate randomization.
Table 1: Primary potential for errors when using DNA as data storage.
Church et al. were the first to suggest that choosing bases randomly (A or C for 0 and T or G for 1) while disallowing homopolymer runs greater than three may overrule any sequence properties that are detrimental to sequencing. Based upon analysis of potential sequencing failure encountered during decoding, Goldman et al. suggested development of a code with no long self-complementary regions [9,10]. They suggested an additional step during encoding whereby the initial message les could be pre-processed either by a one-time pad or other stream cipher with a standard or known key stream. This would lead to DNA segments having random properties, but would be difficult to implement practically. While introducing randomness can be crucial, the problem is how to do this in a way such that accurate decoding can be done without access to the reference message. A one-time pad requires a random key equal to the length of the encoded message and any key stream that is used during message DNA generation needs to be available during decoding. This leads to the problem of how the random key can be made available to the decoding party. As a result, a sophisticated cryptographic scheme would be required to achieve randomness in the stream cipher further requiring a process to store and pass to the decoder a very long key. For long-term data storage these options may limit application.
True randomness is not needed to prevent detrimental structure that impact DNA synthesis and sequencing. In cryptography it is generally important to use good random-number generators but not as important as using good encryption algorithms and key management procedures [11,12]. In practice, therefore, crypto-graphic techniques use secure pseudo-number generators or keystreams. We employ this approach in our multiscale algorithm described below.
The key features of this algorithm can be subdivided into 5 steps. A glossary of abbreviations is given below. These features include (1) Generation of each block as a sequence of nt's that occurs at least R.S-fold and that is randomized by number 7 in step 1. This prevents any detrimental structure that would interfere with sequencing. (2) Randomization is only a function of the base 2 to base 4 conversion and hence, does not require a random key during decryption as it is not a stream cipher or a one-time pad. (3) Each block represents information about data as well as the address and is then further randomized [13]. The code represents each (randomized and expanded) message block mi exactly R times within each DNA segment.
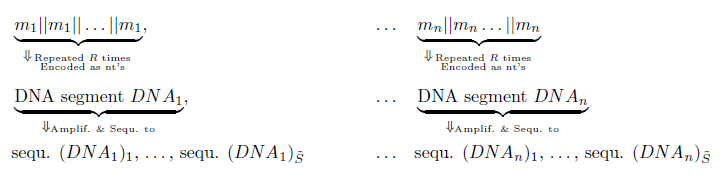
(4) The above is essentially an R.S repetition code. Each of the recovered ≥ S sequences (DNAi)j is made up of a collection of R blocks of mi. (5) The choice of R is dictated by the parameter S as well as the anticipated and required security. Both R and S work in concert.
The larger R is, the more “expensive" in terms of message expansion but is more secure (Figure 1). According to Bellare et al. [7], there was no repetition and some sequences were only recovered once, increasing the probability of error introduction.
Figure 1: The Error Probability during the entire protocol, synthesis and sequencing, versus optimal R value for different S. To correct t substitution errors the Hamming distance of the code, R.S must be ≥ 2t+1. Once S is known, R is chosen accordingly. The gure gives examples of such choices for which all errors in synthesis and sequencing can be corrected. The optimal R value (left) is the R value that maximizes the largest available e ective message length, i.e. the length of each segment Mi. The plot on the right shows the result for our basic encryption scheme, where this length is l/R-lid: In these plots, lid=15 and l=200.
As of Bellare et al. [7] and Buchmann [10] oligonucleotide library is sequenced using next-generation sequencing technologies. The decoding scheme identifies each base of encoded information based on a majority vote of all the read bases corresponding to its position. The final decoding into the message file from the sequencing reads is obtained by exactly reversing the encoding process.
Step 1-encoding
The original text or data are subdivided into equal length blocks. Each block contains both the data part and the corresponding addressing information [14]. Combining both into one block before repetition and sequencing helps to ensure proper placement during decoding.
• Represent the original message M in binary and let len(M) be the length (in characters) of the binary representation of M.
• Let lM be the representation of len(M) in binary, as appropriate pre-pend with zeros to give a fixed length, generate the fixed length binary block M̃=M||0…0||lM by adding in zeros so that the length of M̃ is a multiple of l/R-lid.
• Divide M̃ into pieces M̃i of equal length l/R-lid.
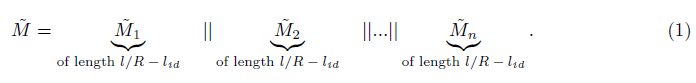
This exactly incorporates all of M̃.
• Let IDbin be a (fixed length) binary string identifying the original file and unique with a given experiment. For each counter i obtained in step 2, find the binary representation of i. Let IDi be the concatenation of IDbin and the binary representation of i. If needed, prepend the latter with zeros to give the fixed length lid for each IDi.
• Incorporate the identifier IDi into each block of Mi to get.
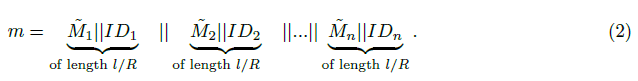
This divides m into equal size blocks m=m1||m2|| ... ||mn where mi=M̃i||IDi.
• Represent each block R times which will give the individual DNA segments of length l, i.e., let
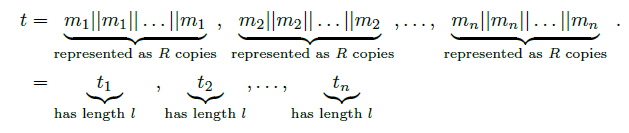
• In the basic scheme we use standard methods to achieve ran5domization. This is generated by the base-2 to base-4 conversion. Generally, given the binary string s=s1s2 ... sn, this gives one of the four values A, C, G, T according to A or C randomly, if si=0 and T or G randomly if si=1 for each i. This randomization is applied here to t=t1, t2,..., tn but with the stronger restriction of avoiding homopolymer runs of length ≥ 2. This gives the base four oligos f1=F (t1), f2=F (t2),..., fn=F (tn) in terms of the four nts A, C, G, T.
Step 1 may be improved via a 7 step process outlined below. The original DNA sequence along with the addressing information is subdivided into blocks of length l [15]. Instead of amplifying and sequencing each block as it contains the base four representation of the data along with their identifiers that might lead to sequencing errors, each of the blocks are masked by some randomizing features. The key to code and decode this randomization is appended to each block. Consequently, both the original part containing the nt and the appended randomizer convert each block into arbitrary sequences with (pseudo) random properties [16]. As random strings, they can be amplified and sequenced. Since representation in base 3 is somewhat more efficient than in base 2, base 3 representation is used, with base 3 to base 4 (i.e., DNA) representation accomplished via the algorithm [10].
• Represent the original message M as a concatenation of base 3 strings that are obtained via the Huffman algorithm and append enough zeros to M to get M̃=M0 ... 0 so that the length of this is a multiple of l/R-lid.-lr. The Huffman step adds further efficiency and uniqueness in decoding. Without it, the length of M, lM needs to be appended, as above (see the example below).
• Split M̃ into pieces M̃i of equal length l/R-lid.-lr.
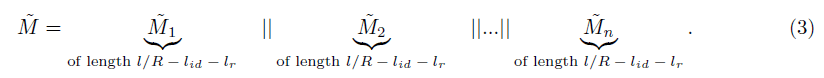
By step 1 this exactly divides out all of M̃.
• Let IDter be a (fixed length) base-3 string identifying the original file and unique with a given experiment. For each counter i obtained in step 2, let IDi be the concatenation of IDter and the base-3 representation of i, the latter pre-pended with zeros as needed to give the fixed length lid for each IDi.
• Incorporate the identifier IDi into each block of M̃i to get the below sequence.
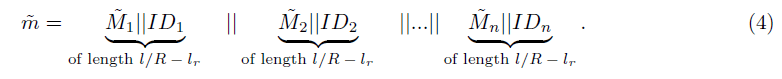
This divides m̃ into equal size blocks m̃ =m̃1||m̃2|| ... ||m̃n.
• For each piece in m̃ chose a random string ri of constant length lr and compute.
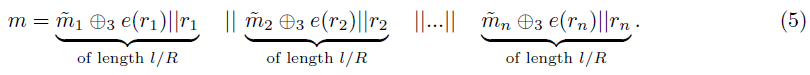
Here, ⊕3 denotes direct sum modulo 3. This divides m into equal size blocks m=m1||m2|| ... ||mn where mi=m̃i ⊕3 e(ri)||ri.
• Represent each block R times, i.e., let
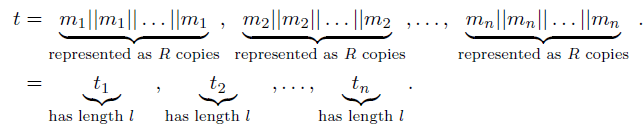
• Represent DNA as A, C, G, T (rather than base 3) using the base-3 to DNA encoding [10].
While step 1 is very easy to apply, the randomization step number 7 in step 1 may not always provide sufficient random effect to avoid any detrimental structures and properties of the obtained nt sequence [17]. Number 7 in step 1 by itself is random, but for longer sequences of, for example, 0's, may still give rise to AC repeats, violating the desired homopolymer condition.
Step 2-generation of DNA
• Determine the code as a collection of DNA segments G(f)=G(f1): ... :G(fn), where G denotes the physical representation and synthesis of DNA corresponding to the design given in segment ti of length l (oligo library synthesis).
• Perform the characterization algorithms (e.g., [4], see [10]) to validate the correctness of the synthesized library.
• Amplify and sequence a sufficient number of copies (i.e., Š times) to ensure that each base of the original message will be recovered at least S times.
Step 3-improved encoding
A cryptographic randomization function is chosen as follows to ensure sufficient randomness in number 7 in step 1-Select a cryptographic expansion function e that takes as input short random strings r and outputs longer (for the algorithm in [10] - ternary) strings e(r) that are random. Select lr the length of the input string r and let the output length be l/R-lr.
For the improved encryption scheme, the repetition also results in a R.S repetition code. The main difference is the randomization via m̃i⊕3e(ri)||ri which makes each component completely (pseudo)-random. This step could be realized in binary (as above), or designed in combination with other codes from coding theory [18]. The Huffman code that we apply has several additional robustness features. The decoding is the reverse of coding protocol. In addition, each m̃i needs to be recovered in (5) by recovering ri and recomputing e(ri). This allows the computation of m̃i from the first part of each mi. Continuing as above this yields M. The original data length does not have to be included but may be. Rather, decoding follows from properties of the Huffman table. Beginning at the first part of M̃ find the corresponding Huffman text words of length 5 or 6 (whichever is found in the Huffman table). Because there is no Huffman code word in the table that consists only of zeros the process terminates when the next block of length 5 or 6 are all zeros.
Using a Huffman code as in Ref. 10 has independent advantages, in addition to what is needed for error correction. It leads to shorter average text lengths than for fixed length codes. Moreover, Hu man code words that are tabulated give additional protection against errors. Indeed, there are a total of 35 +36 ternary words of length 5 or 6, but only a few hundred of these are words used in the table. Finally, it automatically offers additional robustness via the individual word lengths, e.g., the original text length follows from the individual Huffman codewords and does not need to be included explicitly in M̃.
The randomization step provides true pseudo-randomness that should provide adequate scrambling of the nt's to prevent detrimental DNA structure and formation. Each component in the message is a completely random string. Nonetheless the randomization key is automatically obtained during decoding and does not require any additional steps (e.g., sending the key to the decoder) [19]. Different ri's are chosen to avoid the presence of the same part r. Randomization provides a mechanism to identify mutations in living systems. Algorithms described for in vitro applications can be extended to in vivo approaches like [24].
Throughout it is assumed that both R and S are ≥ 1. Thus, after sequencing each original base is recovered at least once, and each block is repeated R ≥ 1 times. As in Ref. 10, the decoding scheme identifies each base of encoded information based on a majority vote of all the read bases corresponding to its position. As each base of encoded information is represented R times, due to their minimal base coverage S, each will be represented R.S time in our R.S repetition code. From this it follows that the minimum distance of our encoding scheme is R.S. Practically, the distribution of the mean number of times each base of encoded information is sequenced and the base coverage follows a normal distribution. In both Refs. 7 and 10, the mean is quite large. The limiting issue is the minimum of these, termed S. Quality control and evaluation of current sequencing algorithms dictates how many sequences need to be generated (i.e., how large Š needs to be) to obtain S>1. These do not correct situations where S=0. This occurred in Ref. 10 and required manual intervention.
Step 4-detection of any errors, including those during message DNA preparation
Using an R.S-fold repetition code as above, allows the detection and correction of many substitution errors during sequencing, storage, and decoding, but it cannot correct errors due to insertion or deletion, or if the error occurred earlier [20], i.e., during message DNA preparation, even when R or S is large. Alternatively, if S=0 for some message bases, as was the case in [10] where the sequencing reaction destroyed two regions of nt's, then the data are lost and cannot be recovered.
In fact, [21] argued that unfortunately there is no system that would provide security and protection against errors that are introduced at the level of message DNA preparation. Such errors cannot be fixed by the synthesis of enough oligos. These types of errors may lead to inaccurate decoding and change the meaning of the recovered message. This would be extremely harmful in situations when the change of meaning is not obvious or when there is no way to assign meaning, as with a cryptographic key or access code.
In such a case it would be desirable, at least, to be aware of such errors. Goldman et al. [10] employed some quality control mechanisms after DNA synthesis, library preparation, and sequencing. They compared the GC content and the k-mer frequencies along the reads with the designed DNA strings. This approach may not be able to detect data loss during the sequencing reaction. It would also not identify errors made during initial message DNA generation. For instance, faulty oligos can mimic a desired GC content and thereby pass the checking routine [10]. The following approaches will address these issues.
• During encoding, append the hash value H(M̃) to M̃.
• During decoding recompute the hash value of the rst part of M̃ and compare it to the given hash value. These values can only agree if no errors had occurred.
In information theory, cryptographic hash functions are a means for ensuring authenticity. For example, they are used to check whether a le has been changed. The hash value of the le is stored separately and the integrity of the le is checked by computing the hash value of the actual le and comparing it with the stored hash value. If the hash values are the same, then the le is unchanged. Secure hash functions have been developed that are mathematically strong in a range of situations [1,6,22].
This step improves the previous algorithms by providing proof if errors occurred during message DNA generation. Practically, hash functions generate a very short output, so the cost in message expansion via H(M̃) is minimal. While it is easy to appended the hash value to M̃, the added number of strings impacts efficiency. Effectively, the available message length is shortened by whatever length the hash value requires. Below, a more efficient approach is described.
Step 5-establishing authenticity of the individual segments
In order to achieve this without knowledge of the message meaning two modifications to the above scheme are needed during encoding.
• Choice of security parameter and identifiers: Let k be a small number, e.g., k=10 or 15 (this will be further described below). Modify number 3 in STEP 3 as follows. Let IDi=IDter||1k||0 ... ||0i3, where i3 is the base- 3 representation of i, prepended with zeros so that IDi is of fixed length lid: The difference to above is that k 1’s are inserted in each identifier. This special structure will be used during a verification step during decoding.
• Computation of m: Update equation (5) as follows:
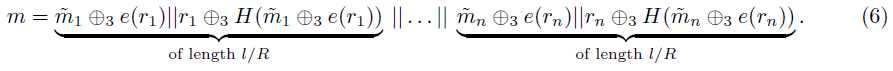
As above, this divides m into equal size blocks m=m1||m2|| ... ||mn , where now mi=m̃i⊕3 e(ri)||ri ⊕3 H(m̃i⊕3 e(ri)).
During decoding, each miis validated for correctness by itself, as follows:
• Define the first l/R- lr digits in mi as m̃i⊕3e(ri).
• Compute the hash value.
• Define ri as the last lr digits in mi subtracted bitwise modulo 3 from the value in step (2).
• Compute e(ri).
• Obtain m̃i via e(ri) from the value obtained in step (1).
• Obtain mi and IDi from each m̃i according to their respective lengths.
• Define z as the k digits in IDi immediately following the (fixed length) identifying info IDter in IDi.
Check if z is a string of k 1's. If so, return i, m̃i and IDter. Otherwise report an error.
Step 5 relies on verifying the final product and proves that this is the original encoded data. Without knowing what the original data are, the algorithm can verify whether the original and final data are the same. The algorithmic security check (number 7 in step 5) will only pass for blocks that are entirely correct. This includes correctness for the data as well as the addressing component. In particular, any nucleotide errors as well as wrong placement will lead to an error message [22]. To find which one is correct, only one string needs to be identified. This idea has been used for various cryptographic applications. It was originally designed for achieving provable optimal asymmetric encryption. That context requires the additional feature of maintaining secrecy. We adapted the underlying premise of this approach to our algorithm. A formal proof of security is given in [5]. In essence, it is impossible to get a valid cipher text, other than starting with the message (i.e., the data to be encoded) and encoding it with the above algorithm.
A necessary condition for the security check in number 7 in step 5 is that all of the encoded part of the block is obtained and decoded correctly. Any error during decoding will almost certainly lead to a decoded value of z that is not all 1's. This is based on the fact that if the decoded value of e(r) or of H(m̃i⊕3e(ri)) and the original value are not the same, then it is unlikely that the random cryptographic functions will result in the desired value of z. A more refined proof (relative to plaintext-awareness) is given in [5].
Any possible error during the entire synthesis process will be detected but may not be corrected at this point. This includes errors during message DNA preparation, or if the sequencing depth for some bases is zero, i.e., if some data were consumed during the process. In our algorithm, the message part contains both the original data component as well as its corresponding indexing information. The check guarantees validity of the data part and establishes that the addressing information will be obtained correctly as the check applies to both; thus, wrong placement is impossible. In particular, the algorithm can verify if the decoded message is the same as the original message, and any nt error or wrong placement will lead to an error message. Typically, with next generation sequencing, there will be numerous correct reads [23]. Even though the original message is never seen, it can be verified as correct. Thus, alignment and comparison are not necessary. When one correct string has been identified, the process of identifying the next correct string can proceed. Finally, on average, this should be a great saving over current alignment based techniques to identify correct strings. Only one correct string needs to be identified. If there is no single correct string, this will be identified quickly by the algorithmic check, in which case majority voting needs to be applied for each base individually.
The price for this security check is the number k of 1's added to IDi. In provably secure cryptographic systems there is considerable uncertainty regarding acceptable limits to k [1,6,13,22]. We suggest k=10 or 15 should be large enough such that a block of 1's is unlikely to be present by chance. The length of k effectively defines the possible length of M̃ and of IDi.
Figure 1 summarizes examples of choices for R and S, illustrating the strengths of the described algorithm steps above without the use of cryptography. Small values of S are included to reflect poor sequencing quality. In reality, S should be much larger, making the schemes more robust. With current technologies, the probability of errors for a DNA sequence is about 1/500 during synthesis, and 1/1000 during sequencing. In [10], the mean error rate per base at the level of sequencing reads was 1/250, which was higher than the combined synthesis and sequencing error rate reported above because of additional errors that were introduced by incorrect indexing.
In information theory, cryptographic hash functions are a means for providing authenticity. Secure hash functions have been developed that are mathematically strong in a range of situations. For example, they are used to check whether a file has been changed. The hash value of the le is stored separately and the integrity of the le is checked by computing the hash value of the actual file and comparing it with the stored hash value. If the hash values are the same, then the file is unchanged.
The incorporation of hash functions improves the previous algorithms by providing proof as to whether errors occurred during message DNA generation. Practically, hash functions generate a very short output, so the cost in message expansion via H(M̃) is minimal.
With current technologies, synthesis and sequencing results in a large pool of correct oligos, or strings. This was confirmed in [10] where after amplification and sequencing the read duplication level was high, providing many reads covering any single string.
Modern sequence alignment algorithms have several challenges. The two most important relate to the enormous amount of short reads generated by next generation DNA sequencing technologies and the appropriate choice of the reference genome, allowing for mismatches and gaps. Contrary to algorithms developed for sequence alignment for DNA, encoding the decoder has no known reference sequence. A large number of reads are received, many with errors. Currently, majority voting for each individual base is used to inform decision making regarding the most likely correct base [24]. The main problem with this approach is the enormous amount of data that need to be stored, compared and evaluated, as well as the problem of systemic errors. We present a solution that does two things. First, it identifies one complete correct sequence among the many assuming that at least one complete correct sequence exists. The main task is to differentiate it from the many without having to analyze enormous numbers of comparisons. Second, we add randomization to deter any systemic errors.
Example: Generally, the value if R is chosen such that R.S is bigger than a required Hamming distance (Figure 1). Here, we use an example for R=3 to illustrate application of the algorithm. If l=198 is the largest integer less or equal to l0=200 for which l/R=66 is an integer. In the example our le identifier has fixed length 3, ternary string IDter:= 021.
Let the message be given in ternary as M=2200212002222221021010011022210122111100211201- 121111210120202212221101001112220000200022101111021012100102120002002001102101212211112021100-010020212000 12000111200210212101110210100112001000220122220112210012110. The length of this is 210 and can be written in ternary as l3:= 210=(21210)3.
Choice of parameters and encoding
• Let lr=5 be the length of the randomizers ri.
• Let lid=17 be the length of the identifier, i.e. the addressing information for each message component.
• Let the fixed length of the ternary representation of lM be lb=8. Recall that lM is l3 prepended with zeros to give this desired length. Here, lM=00021210.
• To obtain M̃, one has to append exactly p zeros to M, such that the length of M plus lb plus p is divisible by (l/R-lid.-lr)=44. Here, 210+8+2=220=5.44 shows that p=2. Therefore, M=M||0000021210, where M is as above in ternary.
• Then n:=len(M̃)=(l/R-lid.-lr) is the number of blocks that will have to be sequenced. Here, len(M̃) is the length of the ternary representation of M and therefore n=220/44=5.
• Let the length of the ternary representation of the internal counter i be 10. This is the counter of the blocks, i.e., i=1,….,n.
• Let the size of the security parameter k be 10. This is the number of, say, 1s that is appended to the counter i inside of each identifier.
This results in n=5 identifiers ID1=02111111111110001, ..., ID5=02111111111110012 which are obtained from IDter=021, appended with the k 1s and the counter i (in ternary) with internal padding to give the fixed length of each IDi to be lid=17.
Specifically, M̃=22002120022222210210100110222101221111002112011211112101202022122211-
0100111222000020002210111102101210010212000200200110210121221111202110001002021200012000- 1112002102121011102101001120010002201222201122100121100000021210 (which is of length 220). Further, when incorporating the specific identifiers including the string of the k 1s, the n=5 internal blocks m̃i are m̃1=22002120022222210210100110222101221 11100211202111111111110001, ..., m̃5=0100112001000220122220112210012110000002121002111111111110012. Each of these has length l/R-lr=61.
Let r1=02000, ...., r5=11211 random ternary strings of length lr=5.
`The expansion function e may be computed via the internal hash function of Maple, by computing the hash of these ri. The output of the hash function is a hexadecimal string of length 32 that can be converted into the corresponding ternary string. To find the e(ri), the ternary representation of hash of ri, H(ri), is chosen for only the first 61=len(m̃i) ternary digits. For instance, H(r1)=82fc813ae79eea7e 3c24af961f59e6cf and therefore e(r1)=1120002022021210101202212012212121211020111122111010120010021.Bitwise addition modulo 3 of m̃i and e(r1) results in 002021102121010112221222000112221002212002202-1222121201120022 which is the first part of m1.
Analogously, the hash of this is now computed via the hexadecimal hash of Maple converted to ternary and then truncated the desired length lr=5. Again, the hash is added bitwise modulo 3 to ri to give the second part of the mi. For instance, H(m̃i⊕3e(r1))⊕3r1=12200. Therefore, e.g., m1=002021102121010112221222000112221002212002202122212120112002212200.
The ti are constructed by repeating each of the mi exactly R=3 times. E.g., t1=00202110212101011222- 122200011222100221200220212221212011200221220000202110212101011222122200011222100221200220212- 2212120112002212200002021102121010112221222000112221002212002202122212120112002212200. Each of the ti has length 3 66=198 which is l, as desired. Finally, each of these is represented in base four via the base-3 to DNA encoding ([10], Table 1) by avoiding homopolymers.
Overall, the result of the encoding part is a list of n=5 DNA segments, e.g., the first being DNA1=CGCGCTCGCTGACTAGATGCTGCAC GTCTGCAGTATGATACATATCATGATCACTCAC-GCAGCACGTATATCTATCAGTCGAGCATCATGTACTCATGACGCAGCGTGCGCTG CAGCTGTCTGTATGATGTACGCGCTCGCTGACTAGATGCTGCACGTCTGCAGTATGATACATATCATGATC ACTCACGCAGCACG.
Decoding
Each of the n segments of the DN Ai is reconverted into their base-3 equivalents.
For example: DNA1 becomes 00202110212101011222122200011222100221200220212221212011200221220000202110212- 10101122212220001122210022120022021222121201120022122000020211021210101122212220001122210022- 12002202122212120112002212200 (which, if correct, is t1). Each of these n recovered segments are then divided into R subcomponents of equal size. For instance, the first component gives the three subpieces 0020211021210101122212220001122 21002212002202122212120112002212200; 002021102121010112221222-000112221002212002202122212120112002212200; 0020211021210101122212220001122210022120022021222-12120112002212200: These should all be the same strings, repeated R=3 times. During decoding, a simple majority vote will compare each of the entries in these R subpieces and return the most likely entry for each individual digit. Here, since there were no errors, only one of these (same) substrings is computed. Doing this for all the n=5 recovered DNA strings yields the original strings m1,…,m5.
This concludes the part of the method that utilizes repetition codes. However, this part may not detect all possible errors. The next steps illustrate how the additional components derived from cryptographic methods address this issue.
Each of the recovered blocks (which should be the mi and which for simplicity are termed mi although it still must be confirmed that they are the same as the original mi) is by itself validated for correctness, as detailed in step 5 as follows.
Let Yi be the last l/R-lr=61 digits for each of the recovered blocks mi. For instance, the Yi recovered from mi is "0020211 021210101122212220001122210022120022021222121201120022". The hash value for this gives "19e30bb67ee7486 df967389903d1487b". This allows for the recomputation of the r1=02000. The expansion function applied to this yields e(r1)=11200020220212101012022120122121212110201111221110-10120010021. Subsequently, m̃1 is recovered as 220021200222222102101001102221012211110021120211111-1111110001.
The crucial step is done via recovering the IDi and testing if they are of the correct form, i.e. with a desired number of 1's. For instance ID1 is recovered as 02111111111110001. The first three digits yield IDter=021 and the next k=10 digits are crucial. If there is no error, the string will be 1111111111, i.e., the test string z of k=10 consecutive 1's. If this test is passed, the entire component mi is therefore proven to be correct [5]. If all the mi are validated then this gives the original message m along with a proof that the recovered m is the same as the original.
Error detection and correction
The internal repetition into R segments constitutes a classic repetition code with straight forward error correcting properties. A simple majority vote will identify less then (R-1)/2 substitution errors. Internal R fold repetition is achieved and is demonstrated above to illustrate the choice of the parameters. However, the strength of our method does not rely on this part and indeed one could achieve strong security even for R=1, due to the cryptography part integrated in step 4 and step 5.
If the size of the security parameter k is large enough then any category of error will be identified during decoding (Table 2). In case of any error, the security check will not pass for a large enough k. For instance, if during decoding the second piece m2 suffers from a deletion at position 3 (after majority decoding), then the decoding routine will recompute the following ID2=0022101122012: It does not end in the desired k ≥ 5 1s and the error is detected.
| Any error(s) corrected during majority decoding | Reconstructed m2 (after majority voting) 0 1 0 1 1 0 1 1 1 1 . . . 0 0 2 0 2 1 1 2 1 0 |
Reconstructed check string "1111111111" |
|---|---|---|
| Example of substitution error | 0 1 2 1 1 0 1 1 1 1 . . . 0 0 2 0 2 1 1 2 1 0 | "2002202000" |
| Example of insertion error | 0 1 2 0 1 1 0 1 1 1 1 . . . 0 0 2 0 2 1 1 2 1 | "0110120120" |
| Example of deletion error | 0 1 1 1 0 1 1 1 1 . . . 0 0 2 0 2 1 1 2 1 0 | "0020122120" |
Table 2 A clearly defined check routine identifies those reads that are error free. Here, these are exactly those for which the check string contains a desired number of 1's. This check will identify all types of errors and identify only those reads that are correct. Details of the implementation and a worked example for correct decoding is given in the example in the text.
According to Bellare et al., it does not matter what type and how many errors occur. Most importantly in order to obtain the desired string of k 1's, the entire message m̃i needs to be recomputed correctly; this is known as “all-or-nothing" security. In order to recover m̃i, one must recover both parts of m̃i in their entirety. The first part is required to recover ri from the second part, and ri is required to recover m̃i from its first part. Since any changed bit of a cryptographic hash completely changes the result, the entire part of m̃i must both be completely recovered. Above, R=3 allows the correction of single substitution errors during majority voting. The extra security feature testing for the k 1's provides an additional feature that identifies any type of error that escaped detection, including substitution, deletion, or insertion errors. It gives a guarantee for those strings that are recovered in their entirety. The list of abbreviations is given in the Table 3.
| Short form | Full form |
|---|---|
| l0 | Largest length of segments chosen that are amenable to manipulation |
| l | l The actual block length of each sequence that is sequenced. l0 ≥ l is chosen according to some technical requirements depending on the required number of repetitions within each block |
| R | R The number of repetitions of the same sequence inside each sequenced block. R is chosen such that R=l is an integer and according to some additional technical requirements detailed below to ensure a required hamming distance |
| lid | Length of the identifier for each message block |
| lr | Length of the input string r |
| IDi | Concatenation of the file identifier and the internal counter |
| S | Sequencing depth. A Parameter that identifies the number of sequences to be recovered |
| M | Original message |
| M1||M2 | Concatenation of strings M1 and M2 |
| M | M appended and padded with additional 0's, resp., the message length, to allow unique decoding. The length of M̃is a multiple of l/R-lid (basic scheme) or of l/R-lid-lr(enhanced scheme) |
| M̃i | The equal length blocks within M̃ |
| mi, m̃i | The individual message blocks with their identifiers, after incorporation of the respective cryptographic steps |
| r, ri | pseudorandom string of length lr |
| e(ri) | A cryptographic expansion function that takes a short random string ri and outputs a longer random string e(ri) |
| m̃i⊕3e(ri)||ri | random string ri of length lr chosen from data m and direct summed ⊕3 modulo 3 with m. Each of these has length l/R |
| H(M) | Hash value of M |
| k | Security parameter underlying the cryptographic OAEP scheme |
| z | Last k digits in m̃i. These k strings are checked for a specific pattern. Used in Step 5 to ensure authenticity of the individual segments |
Table 3: List of Abbreviations.
A multistep algorithm is presented based on cryptographic features that increase precision and security. Two main ingredients are randomization and secure data integrity. The method is flexible and allows for increased levels of security, depending on demand, and identifies approaches to detect and correct errors. This is based on the number of DNA blocks required to be encoded within each generated sequence of DNA (as represented by R), or how many need to be sequenced (as represented by S). In contrast, the Illumina protocol [2] focuses on the average curve of the sequencing depth. In worst case scenarios, i.e., when certain nucleotide bases are consumed during the encoding process, algorithm will detect the loss of these data.
Our approach is applicable to in vitro and in vivo approaches of DNA storage and sequence analysis. Key for both is adequate randomness in the encoding algorithm. In vitro approaches require sufficient redundancy to prevent detrimental DNA sequence and structure. In vivo approaches must avoid the existence of the same or similar copies of DNA within a single cell. The required level of randomization is achieved by tools derived from cryptography that do not rely on knowledge or transmission of secret keys or randomization data. Another potential application of our algorithm is for the identification of genetically modified organ-isms. Effectiveness and accuracy require multiple copies of a trademark DNA label or "barcode" containing authentication and tracking information inside a single cell. This challenge can be efficiently addressed based on the randomization techniques described; each individual segment of DNA represents the same information, but is randomized before being encoded in DNA.
As the algorithm can be applied to validate and verify the correctness of the individually decoded pieces, without knowing the original data, a certificate can be generated that confirms that the obtained data are exactly like the original ones. This has applications to DNA steganography, sequence alignment, and fast identification of correct reads in next generation sequencing.
This work was supported by NSF-40243. The authors declare that they have no competing interests. SM designed and devised the algorithms. DR and FJ supervised the project. All authors contributed to writing of the manuscript and approve of its content.