Research Article - (2018) Volume 6, Issue 1
Safa Ibrahim Adi* and Mohammed Aldasht
Department of Computer, Palestine Polytechnic University, Palestine
Feature selection in high-dimensional datasets is con-sidered to be a complex and time-consuming problem. To enhance the accuracy of classification and reduce the execution time, Parallel Evolutionary Algorithms (PEAs) can be used. In this paper, we make a review for the most recent works which handle the use of PEAs for feature selection in large datasets. We have classified the algorithms in these papers into four main classes (Genetic Algorithms (GA), Particle Swarm Optimization (PSO), Scattered Search (SS), and Ant Colony Optimization (ACO)). The accuracy is adopted as a measure to compare the e ciency of these PEAs. It is noticeable that the Parallel Genetic Algorithms (PGAs) are the most suitable algorithms for feature selection in large datasets; since they achieve the highest accuracy. On the other hand, we found that the Parallel ACO is time-consuming and less ccurate comparing with other PEA.
Evolutionary algorithms, Parallel computing, Classification, Feature selection, High dimensional dataset
Now-a-days many disciplines have to deal with high dimensional datasets which involve a huge number of features. So we need data pre-processing methods and data reduction models In order to simplify input data. There are two main types of data reduction models [1]. The first is: instance selection and instance generation processes are focused on the instance level. (i.e., select a representative portion of data that can fulfil a data mining task as if the whole data is used) [2]. the second is: feature selection and feature extraction models which work at the level of characteristics. These models attempt to reduce a dataset by removing noisy, irrelevant, or redundant features. Feature selection is a necessary pre-processing step in analyzing big datasets. It often leads to smaller data that will make the classifier training better and faster [3].
Feature selection is a problem with big datasets. In order to make classification faster and more accurate, we need to select the subset of features that are discriminative. Evolutionary algorithms like Genetic algorithms, Swarm intelligence optimization, Ant colony optimization, etc. These methods can be e ective for this problem, but they require a huge amount of computation (long execution time), also memory consumption. In order to overcome these weaknesses, parallel computing can be used. In this survey, we will review a set of papers about parallel evolutionary algorithms that used for feature selection in large datasets. Furthermore, we will compare the performance of di erent algorithms and environment. The rest of the paper is organized as follow: Section 2 is Background about feature selection approaches and parallel architecture in general. Section 3 talk about parallel evolutionary algorithms. Section 4 will discuss and review many papers which talk about the feature selection problem by using parallel computing. Section 5 contains the summary of the survey; the last section is the conclusion and future work.
In general, there are three classes of feature selection: filter-based, wrapper, and embedded. The filter approach analyses the features statistically and ignores the classifier. Most of filter-based methods perform two operations, ranking and subset selection. In some cases, these two operations are performed sequentially, first the ranking, then the selection, in other cases only the selection is carried out. These methods are e ective in terms of execution time. However, filter methods sometimes select redundant variables; since they don’t consider the relationships between variables. Therefore, they are mainly used as a pre-processing method. In the wrapper model [4], the process of feature selection is depending on the performance of a specific classifier. But its disadvantages are time-consuming and over fitting. The last method for feature selection is the embedded. In this method, the feature selection process and the learning algorithm (tuning the parameters) are combined to each other [5,6].
Parallel Evolutionary Algorithms for Feature Selection in High Dimensional Datasets
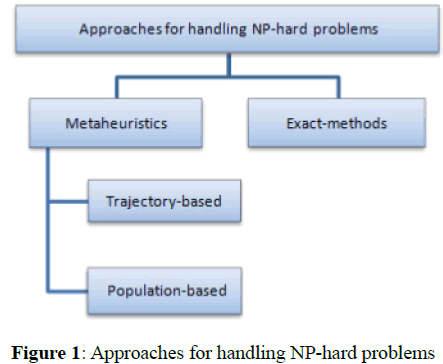
The selection of optimal feature subset is an optimization problem that proved to be NP-hard, complex, and time-consuming problem [7]. Two major approaches are traditionally used to tackle NP-hard problems, as seen in Figure 1, exact methods and met heuristics. Exact methods allow exact solution to be found, but this approach is impractical since it is extremely time consuming for real world problems. On the other hand, metaheuristics are used for solving complex and real world problems. Because metaheuristics provide suboptimal (sometimes optimal) solution in reasonable time [8-10]. Trajectory-based (exploitation-oriented methods): the well-known metaheuristics families based on the manipulation of a single solution. Include Simulated Annealing (SA), Tabu Search (TS), Iterated Local Search (ILS), Variable Local Search (VNS), and Greedy Ran-domized Adaptive Search Procedures (GRASP). Population-based (exploration-oriented methods): the well-known metaheuristics families based on the manipulation of a population of solutions. Include PSO, ACO, SS, Evolutionary Algorithms (EAs), Di erential Evolution (DE), Evolutionary Strategies (ES), and Estimation Distribution Algorithms (EDA). Met heuristics algorithms have proved to be suitable tools for solving the feature selection accurately and efficiently for large dimensions in big datasets [2]. The main problems when dealing with big datasets are: The first is execution time because the complexity of the met heuristics methods for feature selection is at least O (n2 D), where n is the number of instances and D is the number of features. The second is memory consumption since most methods for feature selection need to store the whole dataset in memory. Therefore, the researchers try to parallelize the sequential. Metaheuristics to improve their e ciency for feature selec-tion on large datasets. There are many programming models and paradigms, such as Map Reduce (Hadoop, spark), MPI, Open MP, and CUDA [1,6,11]. Parallel computing can be process interaction (shared memory, message passing) or problem decomposition (task or data parallelization) [6].
Figure 1: Approaches for handling NP-hard problems
Parallel computing is a good solution for these problems since many calculations are carried out simultaneously in the task and/or data [6]. Population-based metaheuristics are naturally prone to parallelize since most of their variation operators can be easily undertaken in parallel [2,11].
Parallel implementations of metaheuristics are an effective alternative to speed up sequential metaheuristics; by reducing the search time for solutions of optimization problems. Furthermore, they lead to the more precise random algorithm and improve the quality of solutions [11].
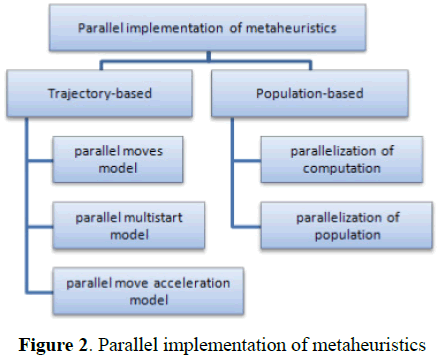
As seen in Figure 2, the implementation of parallel metaheuristics is divided into two categories [12].
Figure 2: Parallel implementation of metaheuristics
Parallel evolutionary algorithms are used in many works rather than feature selection, such as inferring phylogenies, tra c prediction. Santander et al., [9] used MPI/Open MP with a hybrid multiobjective evolutionary algorithm (fast nondominated sorting genetic algorithms and firefly algorithm); for phylogenetic reconstruction (Inferring evolutionary trees). Jiri at al., [10] used parallel multiobjective GA with OpenMP. In order to make tra c prediction more accurate. Master-Slave scheme of GA was implemented on multi-core parallel architecture. They reduced the computational time, but it was successful for short-term tra c prediction.
Overview of Parallel Evolutionary Algorithms for Feature Selection
Feature selection algorithms are used to find an optimal subset of relevant features in the data. In this section we will talk about parallel evolutionary algorithms that are used for feature selection problem in large datasets. We will illustrate the steps of six algorithms (PGA, PCHC, PPSO, PGPSO, PSS, and PACO).
Parallel Genetic algorithm (PGA)
In order to increase the efficiency and reduce the execution time of the genetic algorithm (GA); the researchers used parallel GA. Algorithm 1 presents the parallel GA methodology, with the master-slave model of parallel GA.
Algorithm 1 Parallel genetic algorithm [10]:
A. Create initial population
B. Create slaves
C. while not done do
a Start slave
b Wait for slave to finish
c Run mutation operator
d End while for i=1 to slave iterations do Select individuals Run crossover operator Evaluate offspring’ if solution found then set done=True.
Parallel CHC algorithm (PCHC)
A CHC is a non-traditional GA, which combines a conservative selection strategy (that always preserves the best individuals found so far), that produces o springs that are at the maximum ham-ming distance from their parent. The main processes of CHC algorithm are [1]:
a Half-Uniform Crossover (HUX): This will produce two o springs, which are maximally di erent from their two parents.
b Elitist selection: this will keep the best solutions in each generation.
c Incest prevention: this step prevents two individuals to mate if the similarity between them greater than a threshold.
d The Restarting process: if the specified population stagnated, then this step generated a new population by choosing the best individuals.
Particle Swarm Optimization (PSO)
This sub-section handles the geometric particle swarm optimization (GPSO) and shows the algorithm that used to parallelize PSO or GPSO.
Geometric Particle Swarm Optimization (GPSO)
GPSO is a recent version of PSO. The key issue in GPSO is the using a multi-parental recombination of solutions (particles). In the first phase, a random initial-ization of particles created. Then the algorithm evaluates these particles to update the historical and social positions. Finally, the three parents (3PMBCX) move the particles, as shown in Algorithm 2:
Algorithm 2 GPSO algorithm [2]
S: Swarm Initialization () while not stop condition do do for each particle i of the swarm S do do
Evaluate (solution (xi))
Update (velocity equation (hi))
Update (global best solution (gi))
End for
For each particle i of the swarm S do do
Xi: 3PMBCX ((xi, wa), (gi, wb), (hi, wc))
Mutate (xi)
End for
End while
Output: best solution found
Parallel Multi Swarm Optimization (PMSO)
Parallel multi swarm optimization presented in [2], it was defined in analogy with parallel GA as a pair of (S, M), where S is a collection swarm and M is a migration policy. Algorithm 3 depicts the parallel PSO methodology.
Algorithm 3 Multi swarm optimization [2]
Do In Parallel for each i â´L´L 1,..., m
Initialize (Si)
While not stop condition do do
Iterate Si for n steps /* PSO evolution */
For each Sj â´L´L Ï ˇ D (Si) do do
Send ÏA˛ particles in ÏE˛s (Si) to Sj
End for
For each Sj such that Si â´L´L Ï ˇ D(Sj ) do do
Receive ÏA˛ particles from Sj
Replace ÏA˛ particles in Si according to ÏE˛r
End for
End while
Output: best solution ever found in the multiswarm
Parallel Scatter Search (PSS)
Scatter search is an evolutionary method that was successfully applied to hard optimization problems. It uses strategies for search diversification and intensification that have proved effective in a variety of optimization problems, see Algorithm 4.
Algorithm 4 Parallel scatter search methodology [11]:
Create Population (Pop, Pop Size)
Generate Reference Set (RefSet, RefSetSize)
While Stopping Criterion 1 do
While Stopping Criterion 2 do
Select Subset (Subset, Subset Size)
For each processor r=1 to n do in parallel do
Combine Solutions (Subset, Cur Sol)
Improve Solution (Cur Sol, Imp Sol)
End for
End while
Update Reference Set (RefSet)
End while
Parallel Ant Colony Optimization (PACO)
When dealing with huge search space, parallel computing techniques usually applied to improve the e ciency. Parallel ACO algorithms can achieve high-quality solutions in reasonable execution times comparing with sequential ACO [13]. In Algorithm 5, the methodology of PACO is presented.
In Algorithm 5 Parallel ant colony optimization methodology [14-18]
Generate Ants
Initialize N processors
Multicast to all slaves’ processors N and the task ids of all slaves for each slave do do
Send a number between 0 and N that identifies the task inside the program
End for
While not all slaves have sent back solution do
Wait for solution
If a slave returns a solution that is better than any solution
Received then
Multicast this solution to all slaves
End if
End while
Return the best solution
Algorithm 5 Parallel ant colony optimization methodol-ogy [14]
Parallel evolutionary algorithms for feature selection
We reviewed a set of research papers, which were dealing with feature selection problem for high dimensional datasets in a parallel environment and using parallel evolutionary algorithms. Let us discuss these studies in the following subsections.
Parallel GA
Liu et al. [10] used parallel GA for selecting informative genes (features) in tissue classification, using wrapper approach. The main purpose was to find the subset of features with fewer elements and higher accuracy. The parallelization of GA performed by dividing the population into subpopulations, and then the GA run on each subpopulation. Therefore, the searching for the optimal subset of genes can be on several CPUs/ computers at the same time.
For evaluation, the Golub classifier was used. This classifier introduced by the authors and it depend on the sign of the results for classification; if the sign is positive the sample x belongs to class 1; else if it negative the sample x belongs to class 2. This classifier used only if the datasets have two classes. The accuracy of the classifier tested by using the LOOCV (leave one out cross validation) method. The results showed that using the parallel GA increased the accuracy, and reduced the number of genes that used for classification. Zheng et al., [15] analysed the execution speed and solution quality of many parallel GA schemes theoretically. Furthermore, they pointed to the best scheme of parallel GA that used on multi-core architecture. This paper considered the relationship between speed and parallel architecture along with solution quality.
Zheng et al., [8] analysed the execution speed and solution quality of many parallel GA schemes theoretically. Furthermore, they pointed to the best scheme of parallel GA that used on multi-core architecture. This paper considered the relationship between speed and parallel architecture along with solution quality. They analysed (Master- Slave, Synchronous Island, Asynchronous Island, Cellular, and hybrid scheme of Master-Slave and Island) schemes of parallel GA, with Pthread library on multi-core parallel architecture.
To validate their theoretical analyzing experiments performed. The hybrid scheme of (Master-Slave and Asynchronous Island) was the best scheme in performance using multi-core architecture. The Island scheme has the best execution time, but the worst solution quality. To improve the solution quality when using Island models it is better to decrease the number of islands. The Asynchronous Island is faster than the Synchronous. The Master- Slave scheme has the best solution quality and the worst execution time.
Soufan et al., [16] developed a web-based tool called DWFS, which used for feature selection for di erent problems. This tool followed a hybrid approach of wrapper and filter. First, the filter used as pre-processing and select the top ranked features based on tunable and a predefined threshold. In the next step, parallel GA based on wrapper approach applied to the selected features to search for subset features that increase the classifier accuracy. The scheme of parallel GA was Master-Slave; the master node used to create initial population and GA steps. While the slave (worker) nodes used for fitness evaluation of each chromosome, this implementation is performed on 64 cores.
For evaluation, they used three di erent classifiers (Bayesian classifier, K-nearest neighbour, and a combination of them). The results of the experiments show that DWFS tool provided many options to enhance the feature selection problem in di erent biological and biomedical problems.
Pinho et al., [7] presented a framework called Par-JEColi (java-based library) for a parallel evolutionary algorithm in bioinformatics applications. The aim of this platform was to make the parallel environment (multi-core, cluster, and grid) easy and transparent to the users. This library adapted itself to the problem and the target parallel architecture. The user can easily configure the parallel model and the target architecture; since, ParJEColi encapsulated the parallelization concerns as features. The explicit steps implemented by a simple GUI.
The experiments for validation this framework was done on 2 biological dataset and many bioinformatics scenarios. The results indicate that the proposed framework improves the computational performance (decreases execution time) also the solution quality.
Parallel CHC
Peralta et al., [1] presented a parallel evolutionary algorithm called CHC algorithm by using the Map Reduce paradigm for selecting features in high dimensional datasets to improve the classification. The parallelization of CHC algorithm is done by using Map Reduce procedure (Hadoop implementation).
A cluster of computers of 20 computing nodes were used. Each dataset split into 512-map task. For evaluating their work, three classifiers where used SVM (support vector machine), logistic regression, and Bayesian classifier.
The results showed that the run time for classification increased as the number of features decreased, except for Bayesian classifier. They explained this result as follow: if the number of blocks less than the number of computing machines; this leads to have some machines remain idle. In addition, if the number of blocks greater than the number of computing machines, the blocks maybe will not distributed in efficient way.
They compared parallel CHC with the serial version, and they concluded that the accuracy of classification increased by using parallel CHC. Furthermore, the parallel version of CHC reduced the run time when the datasets is high dimensional.
Parallel PSO
PSO is an efficient optimization technique; it used to solve the problem of feature selection in high dimensional datasets. In [4] Chen et al. used the parallel PSO algorithm for solving two problems at the same time. By creating an objective function that takes into account three variables at the same time (the selected features, the number of support vectors, and average accuracy of SVM) in order to maximize the capability of SVM classifier in generalization.
The proposed method called PTVPSO-SVM (parallel time variant particle swarm optimization support vector machine), it had two phases: 1) The parameter settings of SVM and feature selection work together. 2) The accuracy of SVM evaluated using the set of features and the optimal parameters from the first phase.
They used parallel virtual machine (PVM) with 8 machines; and 10-fold cross validation. The results showed that they could achieve the following aims: increasing the accuracy classification, reducing the execution time comparing with sequential PSO, producing an appropriate model of parameters, and selecting the most discriminative subset of features.
Feature selection can be carried out based on rough set theory with searching algorithm as reported in [3,6]. Qian et al., [6] proposed three parallel attribute reduction (feature selection) algorithms based on Map Reduce on Hadoop. The first algorithm was built by constructing the proper (key, value) by rough set theory and implementing Map Reduce functions. The second algorithms were done by realizing the parallel computation of equivalence classes and attribute significances. The last parallel algorithm was designed to acquire the core attributes and reduces in both data and parallel task.
The experiments are performed on a cluster of computers (17 computing node). They considered the performance of the parallel algorithms, but they did not focus on the classification accuracy; since the sequential and parallel algorithms gave the same results. The results showed that the proposed parallel attribute reduction algorithms could deal with high dimensional datasets in an efficient way and better than the sequential algorithms.
Adamczyk [3] used rough set theory for attribute reduction, to increase the e ciency he implemented parallel Asynchronous PSO for this problem. The parallelization was done by assigning the complex function computations in slave cores and the main core make the updating particle and checking the convergence of the algorithm.
Parallel evolutionary algorithms for feature selection in high dimensional datasets
From their experiments it was noticeable that the e - ciency and speedup of parallel PSO algorithm were raising as the size of dataset increased. The achievable accuracy was not astonishing, but it was better than the classical algorithms.
Parallel GPSO
Garcia-Nieto et al., [2] parallelized a version of PSO called GPSO which is suitable for feature selection problem in high dimensional datasets. The proposed method was called PMOS (Parallel multi-swarm optimizer) which was done by running a set of parallel sub PSOs algorithms, which forming an island model. Migration operation exchanged solutions between islands based on a certain frequency. The aim of the fitness function increasing the classification accuracy and reduce the number of selected genes (features).
They used the SVM classifier (Support Vector Machine) to prove the accuracy of the selected subset of features. In their experiments, they used a cluster of computers as a parallel architecture. They found that 8-swarm PMSO was the best choice for parallelization. The results pointed out that this algorithm was better than the sequential version and other methods in term of performance and accuracy while it selected few genes for each subset.
Parallel SS
Lopez et al., [11] present a parallel SS metaheuristics for solving feature selection problem in classification. They proposed two methods for combining solutions in SS. The first method is called GC (greedy combination): in this strategy, the common features of the combined solutions are added, and then at each iteration, one of the remaining features is added to any new solution. The second strategy is called RGC (reduced greedy combination), it has the same start as GC, but in the next step, it considers only the features that appear in solutions with good quality. Then the parallelization of SS is obtained by running these two methods (GC, RGC) at the same time on two processors using different combination methods and parameters settings at each processor.
They compared the proposed parallel SS with sequential SS and GA. The results show that the quality of solution in parallel SS is better than solutions which were obtained from the sequential SS and GA. Also, the parallel SS use a smaller set of features for classification. The run time is the same for parallel and sequential SS.
Parallel ACO
This subsection shows how the parallel ACO is used to solve feature selection problem for classification in high dimensional datasets. Meena et al., [18] implemented a parallel ACO to solve the feature selection problem for long documents. The parallelization was done using Map Reduce programming model (Hadoop) that automatically parallelize the code and data then run them on a cluster of computing nodes. The wrapper approachis used as evaluation criteria that used Bayesian classifier. Furthermore, the accuracy of the classifier was based on these metrics: precision, recall, accuracy and F-measure. The enhanced algorithm (parallel ACO) was compared with ACO, enhanced ACO, and two feature selection methods, CHI (Statistical technique) and IG (Information Gain). They used Bayesian classifier in evaluation process. The results showed that for a given fixed quality of the solutions the proposed algorithm could reduce the execution time but without considered the solution quality. On the other hand, the accuracy of the classifier was increased using parallel ACO comparing with sequential ACO and feature selection methods.
Cano et al., [12] parallelized an existing multiobjective ant programming model that used as the classifier. This algorithm was used for rule mining in high dimensional datasets. The parallelization was done on data and each ant encoded a rule. This was achieved by let each processor perform the same task on a di erent subset of the data at the same time. In the implementation, they used GPUs, which are multi-core and parallel processor units architecture. This parallel model Followed CUDA method.
For evaluation they used these metrics: true positive, false positive, true negative, false negative, sensitivity, and specificity. The results indicate that the e ciency of this model was increased as the size of datasets increased.
The summary of the papers that implemented the parallel EA for solving the classification problem in high dimensional datasets is reported in Table 1 and Table 2.
| Paper | Used evolutionary algorithm | Parallel Programming model |
|---|---|---|
| Peralta et al. [1] | CHC (Type of GA) | Map Reduce |
| Garcia-Nieto et al. [2] | GPSO | MALLBA |
| Adamczyk [3] | PSO | Unknown |
| Chen et al. [4] | PSO | PVM |
| Liu et al. [5] | GA | Unknown |
| Lopez et al. [11] | SS | Unknown |
| Meena et al. [17] | ACO | Map Reduce |
Table 1: Summary of algorithms and programming models
| Paper | dataset | Classifiers | Metrics for classification | Accuracy |
|---|---|---|---|---|
| Peralta et al. [1] | Epsilon | Bayesian | AUC= (TPR+TNR)/2 | 0.71 |
| SVM | 0.68 | |||
| 0.70 | ||||
| Logistic Regression | ||||
| 0.67 | ||||
| ECBDL 14-ROS | Bayesian | |||
| 0.63 | ||||
| SVM | ||||
| Logistic Regression | 0.63 | |||
| Garcia- Nieto et al. [2] | Colon | SVM | Success Rate | 0.85 |
| Lymp | 0.97 | |||
| Leuk | 0.98 | |||
| Lung | 0.97 | |||
| Adamczyk [3] | 15 Data Set | Success Rate | 0.70 (Avg) | |
| Chen et al. [4] | 30 Data Set | Success Rate | 0.87 (Avg) | |
| Liu et al. [5] | Leukemia | Golub | Success rate | 0.88 |
| Colon | N/A | |||
| Lopez et al. [11] | 12 Data Set | Nearest Neighbor | Success rate | 0.86 (Avg) |
| 0.87 (Avg) | ||||
| Bayesian | ||||
| 0.86 (Avg) | ||||
| Soufan et al. [15] | 9 Data Set | K- Nearest Neighbor | F1, PPV, GMean | 0.81(Avg) (GMean) |
| Bayesian | 0.79(Avg) (GMean) | |||
| Meena et al. [17] | 2 Data Sets | Bayesian | F-measure, recall | 0.64 (Avg) |
Table 2: Summary of datasets, classifiers, and accuracy results
Many research papers [2,3,7-12], stated that we can reduce the execution time and achieve acceptable speed ups, when applying parallel evolutionary algorithms on multiple processors. We noticed that they achieved a reasonable speed up in many cases.
In the next table (Table 2), when comparing the accuracy of parallel EA it is important to notice how many classifiers were used to measure the accuracy. Furthermore, we should consider the metrics that were used to evaluate the classifier. For example, the parallel PSO and its variants have the higher accuracy; but they used only one metric which is the success rate. This means that the parallel PSO is not the most accurate parallel EA based on Table 2.
On the other hand, the parallel GA and its variant has the least accuracy, but they used from two to five metrics for evaluation purpose. Based on these metrics, we can say that the parallel GA is the best parallel EA for feature selection in high dimensional datasets
After the review of different parallel EA that are used to solve the feature selection problem in high dimensional datasets. We adopted the accuracy as a measure to compare the algorithms performance.
The following points show our conclusion about the per-formance of the mentioned algorithms in this chapter for feature selection:
GA and its variants: based on the papers we reviewed, the parallel GA has the higher accuracy.
PSO and its variants: the parallel PSO has the same accuracy as sequential PSO.
SS: parallel SS gives better results in case of accuracy than GA and sequential SS.
ACO: parallel ACO has the less accurate results than the other parallel EA.
It is noticeable that PGAs are the most suitable algorithms for feature selection in large datasets; since they achieved the highest accuracy. On the other hand, the PACO is time-consuming and less accurate comparing with other PEA.
