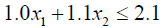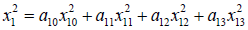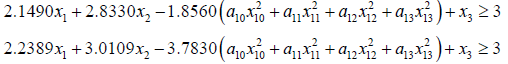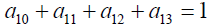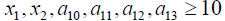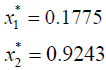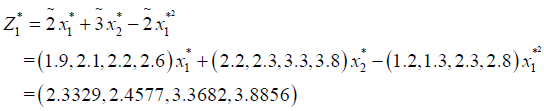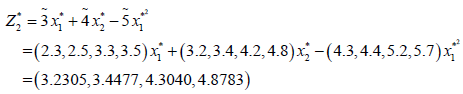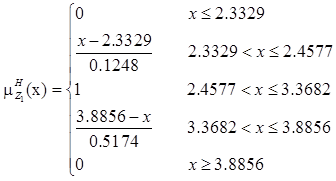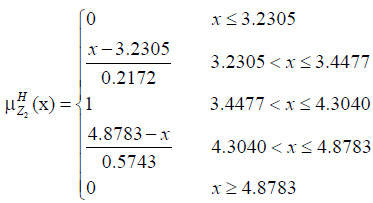Keywords
Hyperbolic membership function; Fuzzy multi-objective nonlinear programming problem; Ranking function
Introduction
The real world problems with multiple conflicting objectives are more conveniently modeled into multi-objective programming problems. Further, when the parameters are imprecise numerical quantities, it is very much appropriate to implement fuzzy quantities for modeling these situations. In 1970, Bellmann and Zadeh introduced the concept of fuzzy quantities in decision making. Authors like H.R. Maleki, A. Ebrahimnejad et al., P. Fortemps et al., H. Zimmerman have introduced fuzzy programming approach to solve crisp multi-objective linear programming problem. In 1981, Leberling used a nonlinear membership function in form of hyperbolic function for solving linear programming problem. In 1991, Dhingra et al. introduced exponential, quadratic and logarithimic membership functions for optimal designing problems. In 1997, R. Verma et al. used the fuzzy programming technique based on some nonlinear membership function to solve fuzzy MOLPP. R. B. Dash et al. used defuzzification through ranking function and Zimmerman’s technique based on trapezoidal membership function for solving fuzzy MOLPP. P. Rath et al. used exponential and hyperbolic membership functions in Zimmerman’s technique to solve fuzzy MOLPP. Recently P. Rath et al. extended the idea of their paper and solved fuzzy multi-objective nonlinear programming problem (FMONLPP) through exponential membership function [1-17]. In this paper, after defuzzification of FMONLPP, the resulting nonlinear multi-objective programming problem is solved using Zimmerman’s technique through hyperbolic membership function. Also, the nonlinear terms occurring in the Zimmerman’s procedure are linearalised to marginalize the intricacy. A numerical example is given for better understanding of the technique.
Fuzzy Multi-objective Nonlinear Programming Problem (FMONLPP)
We consider fuzzy multi objective nonlinear programming problem with trapezoidal fuzzy coefficients as follows
Max 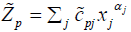 p=1, 2…q
p=1, 2…q
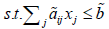 i=1,2…m (2.1)
i=1,2…m (2.1)
where 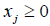
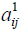 and
and 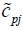 and are in the above relation are in trapezoidal form as
and are in the above relation are in trapezoidal form as
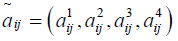
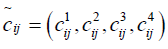
Now the FMONLPP can be transformed to a MONLPP by applying the Rouben’s ranking function R as below.
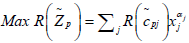 p = 1, 2…q
p = 1, 2…q
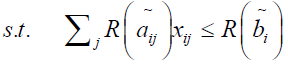 i = 1, 2…m
i = 1, 2…m
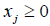
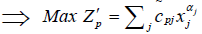 p=1, 2…q
p=1, 2…q
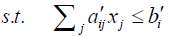 i=1, 2…m (2.2)
i=1, 2…m (2.2)
Where 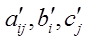 are real numbers corresponding to the fuzzy numbers
are real numbers corresponding to the fuzzy numbers 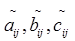 with respect to the exponential function respectively and the Rouben’s ranking function is given below.
with respect to the exponential function respectively and the Rouben’s ranking function is given below.
Rouben’s ranking function
The ranking function suggested by F. Rouben is defined by
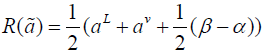
where 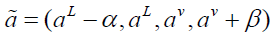
Lemma 1
The optimum solutions of (2.1) and (2.2) are equivalent.
Proof
Let M1, M2 be set of all feasible solutions of (2.1) and (2.2) respectively.
Then x ∈ M1
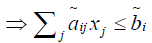 i=1, 2…m
i=1, 2…m
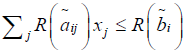
(By applying the Rouben’s ranking function) i=1, 2…m
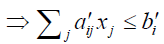
⇒ x ∈ M2
Converse can be proved similarly.
Thus, M1=M2
Let x* ∈ X be the complete optimal solution of (2.1).
Then 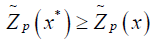 for all x ∈ X, where X is the set of feasible solutions.
for all x ∈ X, where X is the set of feasible solutions.
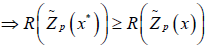 (By applying the Rouben’s ranking function)
(By applying the Rouben’s ranking function)
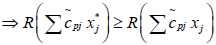
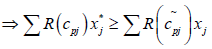 j=1, 2…q
j=1, 2…q
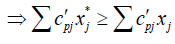 j=1, 2…q
j=1, 2…q
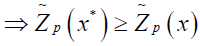 ∀x
∀x
Modified fuzzy programming technique
We modified the Zimmermann’s technique using hyperbolic membership function in order to solve multi-objective nonlinear programming problem (2.2).
Step-1:
The multi-objective linear programming problem is solved by considering one objective at a time and ignoring all others. The process is repeated q times for q different objective functions.
Let X1, X2,…Xq be the ideal situations for the respective functions.
Step-2:
A pay-off matrix of size q by q is formed using all the ideal solutions of step-1. Then from pay-off matrix lower bounds (Lp) and upper bounds (Up) of the objective functions are obtained.
Thus 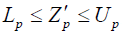 p=1, 2,…q
p=1, 2,…q
Step-3:
Using hyperbolic membership function, an equivalent crisp model for the fuzzy model can be formulated as follows:
Min λ
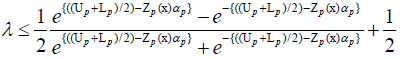 p=1, 2…q
p=1, 2…q
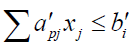 i=1, 2...m
i=1, 2...m
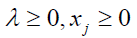 j=1, 2…n
j=1, 2…n
After simplification, the above problem reduces to
Min xmn+1
Subject to
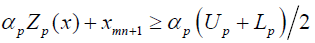 p=1, 2…q
p=1, 2…q
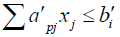 i=1, 2...m
i=1, 2...m
xj ≥0, j=1, 2…n
xmn+1 ≥0
Where 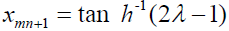
Step-4:
The crisp model is solved and the optimal compromise solution is obtained. The values of objective functions at the compromise solution are obtained.
Numerical example
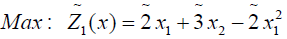
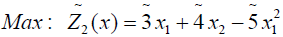 (3.1)
(3.1)
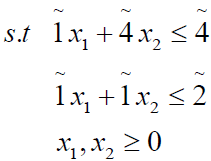
where
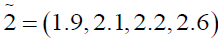
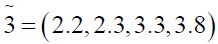
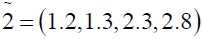
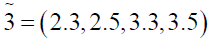
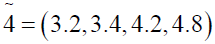
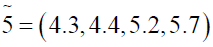
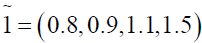
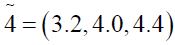
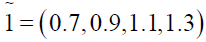
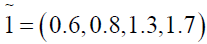
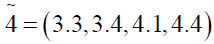
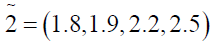
Using ranking function, the problem reduces to
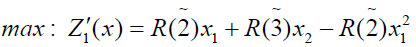
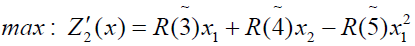
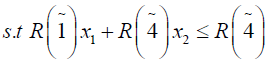
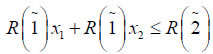
x1, x1 ≥ 0
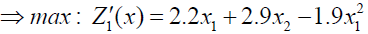 (3.2)
(3.2)
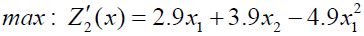 (3.3)
(3.3)
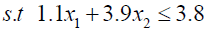
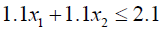
Solving (3.2) and (3.4) by Wolf’s method we get
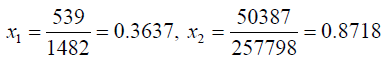
Solving (3.3) and (3.4) by Wolf’s method, we get
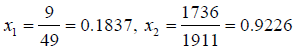
The pay-off matrix of Lower Bounds (L.B.) and Upper Bounds (U.B.) of the objective functions Z′1 and Z′2 is given below
| Function |
LB |
UB |
| Z′1 |
3.0655 |
3.00770 |
| Z′2 |
3.8065 |
3.9653 |
The crisp model can be formulated as
Min x3
Subject to
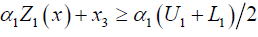
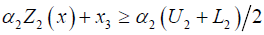
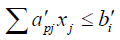
j =1, 2...m (3.5)
j =1,2...n
Putting the values of 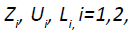 we get
we get
Min x3
s.t.
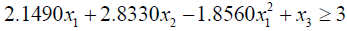
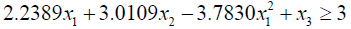
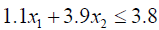 (3.6)
(3.6)
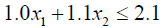
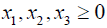
Due to presence of non-linear term x12 in the constraint (3.6), the problem becomes too complex to solve. To avoid the situation taking advantage of
0.1837 ≤ x1 ≤ 0.3637
We linearize x12 as follows.
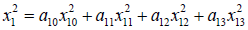
Where
x10 = 0.1837
x11 = 0.2437
x12 = 0.3037
x13 = 0.3637
Then the problem (3.6) reduces to
Min: x3
s.t.
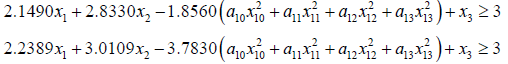
1.1x1 + 3.9x2 ≤ 3.8 (3.7)
1.0x1 +1.1x2 ≤ 2.1
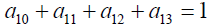
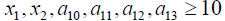
Solving (3.7) the optimal solution of the problem is obtained as:
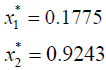
Now the optimal value of the objective functions of FMOLPP (4.1) becomes
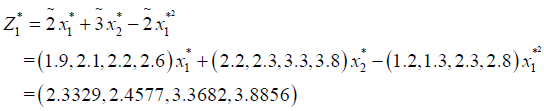
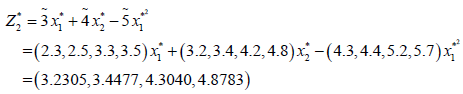
The membership functions corresponding to the fuzzy objective functions are as follows.
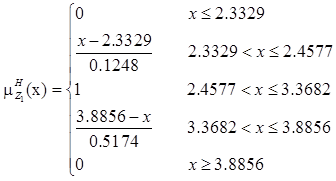
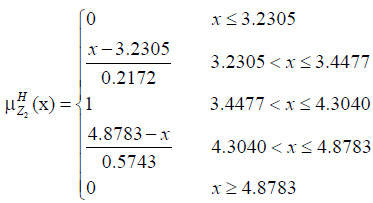
Conclusion
The closeness of the result of the numerical example of this paper with that of the previous paper [17] confirms that the method given in this paper is an alternative way of solving fuzzy multi-objective nonlinear programming problem.
References
- Bellman RE, Zadeh LA (1970) Decision making in fuzzy environment. Management Science 17: B141-B164.
- Zimmermann HJ (1976) Description and optimization of fuzzy systems. Inter J General Systems 214: 209-215.
- Zimmermann HJ (1978) Fuzzy programming and linear programming with several objective functions. Fuzzy Sets and Systems 1: 45-55.
- Liberling H (1981) Fuzzy Sets and System 6: 105-118.
- Campos L, Munoz A (1989) A subjective approach for ranking fuzzy numbers. Fuzzy Sets and Systems 29: 145-153.
- Dhingra AK, Moskowitz H (1991) European J Opex Res 55: 348-361.
- Fortemps P, Roubens F (1996) Ranking and defuzzyfication methods based on area compensation. Fuzzy Sets and Systems 82: 319-330.
- Verma R, Biswal MP, Biswas A (1997) Fuzzy programming technique to solve multi-objective transportation problems with some non-linear membership functions. Fuzzy Sets and Systems 91: 37-43.
- Delgado M, Vila MA, Voxman W (1998) On a canonical representation of fuzzy numbers. Fuzzy Sets and Systems 93: 125-185.
- Maleki HR (2002) Ranking functions and their application to fuzzy linear programming. Far East J Math Sci 43: 183-301.
- Mishmast Nehi M, Laneghad MA (2008) Solving interval and fuzzy multi objective linear programming by necessary efficiency points. Int Math Forum 3: 331-341.
- Ebrahim Nijad A, Nasseri SH (2009) Using complementary slackness property to solve linear programming with fuzzy parameters fuzzy information and engineering 3: 233-296.
- Dash RB, Dash PDP (2011) Solving fuzzy multi objective linear programming problem using Fuzzy Programming Technique. J Odisha Mathematics Society 30: 109-120.
- Rath P, Dash RB (2016) Solution of fuzzy multi-objective linear programming problems using fuzzy programming techniques based on hyperbolic membership function. J Computer and Mathematical Sci7: 653-662.
- Rath P, Dash RB (2017) Solution of fuzzy multi-objective linear programming problems using fuzzy programming technique based on exponential membership functions. Inter J Mathematics Trends and Tech 41: 289-292.
- Dash PDP, Dash RB (2013) Solving fuzzy multi-objective nonlinear programming problem using fuzzy programming technique. Int J Engg Sci and Innov Tech 2: 137-142.
- Rath P, Dash RB (2017) Solution of fuzzy multi objective non-linear programming problem using fuzzy programming technique based on exponential membership functions. Inter J Mathematics Trends and Tech 41: 289-292.

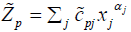 p=1, 2…q
p=1, 2…q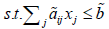 i=1,2…m (2.1)
i=1,2…m (2.1)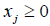
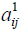 and
and 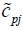 and are in the above relation are in trapezoidal form as
and are in the above relation are in trapezoidal form as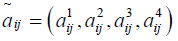
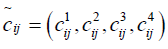
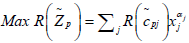 p = 1, 2…q
p = 1, 2…q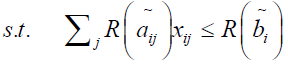 i = 1, 2…m
i = 1, 2…m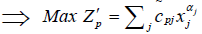 p=1, 2…q
p=1, 2…q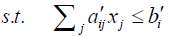 i=1, 2…m (2.2)
i=1, 2…m (2.2)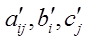 are real numbers corresponding to the fuzzy numbers
are real numbers corresponding to the fuzzy numbers 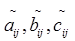 with respect to the exponential function respectively and the Rouben’s ranking function is given below.
with respect to the exponential function respectively and the Rouben’s ranking function is given below.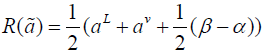
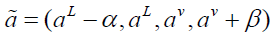
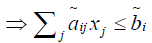 i=1, 2…m
i=1, 2…m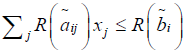
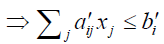
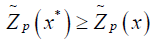 for all x ∈ X, where X is the set of feasible solutions.
for all x ∈ X, where X is the set of feasible solutions.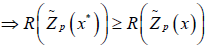 (By applying the Rouben’s ranking function)
(By applying the Rouben’s ranking function)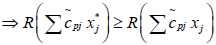
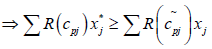 j=1, 2…q
j=1, 2…q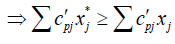 j=1, 2…q
j=1, 2…q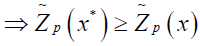 ∀x
∀x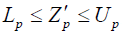 p=1, 2,…q
p=1, 2,…q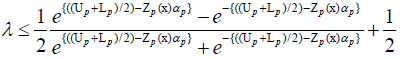 p=1, 2…q
p=1, 2…q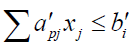 i=1, 2...m
i=1, 2...m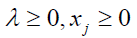 j=1, 2…n
j=1, 2…n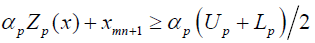 p=1, 2…q
p=1, 2…q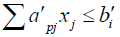 i=1, 2...m
i=1, 2...m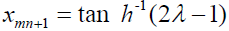
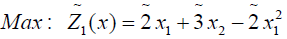
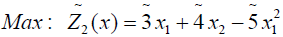 (3.1)
(3.1)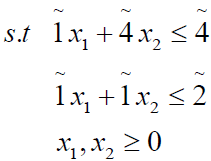
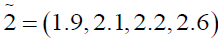
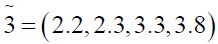
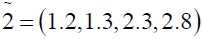
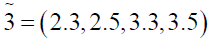
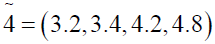
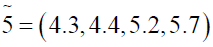
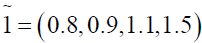
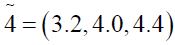
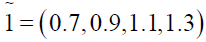
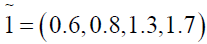
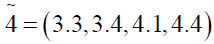
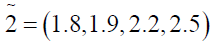
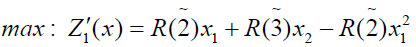
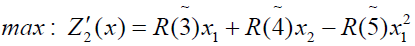
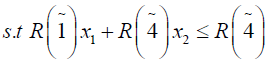
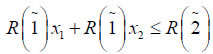
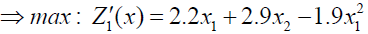 (3.2)
(3.2)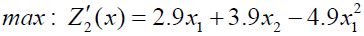 (3.3)
(3.3)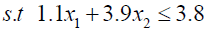
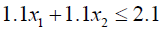
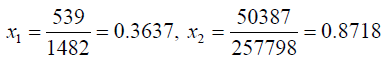
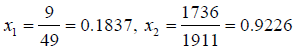
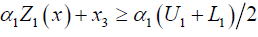
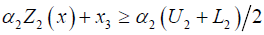
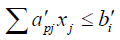
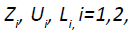 we get
we get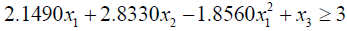
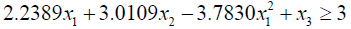
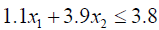 (3.6)
(3.6)