Research Article - (2021) Volume 12, Issue 6
Shyamkant Anwane*
Department of Physics, Shri Shivaji Education Society, Amravati's Science College, Congress Nagar, Nagpur, India
Received Date: January 10, 2021; Accepted Date: March 11, 2021; Published Date: April 06, 2021
Citation: Anwane SW (2021) Special Relativity using Perplex Numbers. Adv Appl Sci Res Vol. 12 No. 4:16.
Imaginary numbers are not merely a part of mathematical jugglery they are of relevance in the real world too. Mathematical models involving real-time and imaginary space are efficient in predicting observable effects and beyond. This research paper aims to reformulate the special relativity using perplex numbers or split complex numbers also known as hyperbolic complex numbers which mankind has been familiar with even before we knew about relativity. Hypotheses that time is real and space is imaginary offers a new look at the space-time fabric. The invariant quantities in special relativity are of hyperbolic formats. This eventually leads to hyperbolic geometry that supports the basic structure of equations. Therefore, the use of hyperbolic complex numbers or perplex numbers handles all perspectives of special relativity with elegance and offers a great degree of simplicity so that even with a meager knowledge of mathematics allows the reader to handle special relativity. The findings support the hypothesis that time is real and space is imaginary in perplexes number representation. A few applications of special relativity in the realm of Quantum Mechanics and Nuclear Physics viz Berkley Collider, Compton’s Effect, Quantum Doppler Effect have been successfully explored.
Berkeley collider; Complex numbers; Compton's effect; energy; Perplex number; Quantum Doppler effect; Special relativity
The complex number system is at the heart of complex analysis and has enjoyed more than 150 years of intensive development along with finding applications in diverse areas of science and engineering. Perplex Numbers are also known as Split Complex numbers or double numbers that have reported applications in explaining many concepts in Physics. Recently in 2003, Bracken and Hayes [1] reported an effective use of perplex numbers for Klein-Gordon equation.
At the beginning of the Twentieth Century, Albert Einstein [2] developed his theory of special relativity, built upon Lorentzian geometry, yet at the end of the century, almost all high school and undergraduate students were still taught only Euclidean geometry. Partly, the reason for this state of affairs has been the lack of simple mathematical formalism in which the basic ideas can be expressed. This research paper claims the formulation of special relativity in perplex numbers configuration that proficiently encompasses the subject elegantly and its consequences with profound simplicity. However, in literature, we find wide reporting of the use of perplex numbers or split complex numbers or hyperbolic geometry concepts for Special Relativity [3-6]. Although the use of perplex numbers is not innovative in this era, the present work attempts to prove the advantage of novel definitions using perplex numbers. Lorentz transformation equations are configured in terms of a single perplex equation. This research paper proposes new definitions of perplex kinematic parameters and its consequent exploration by proper time differentiations and complex conjugate multiplication. New tools are also defined using perplex numbers. Moreover, the proposed approach offers the simplest possible descent to relativistic energy equation while it preserves all consequences of relativity. A couple of applications of SR in the realm of Quantum Mechanics and Nuclear Physics have been are explored for testing the validity as hands-on experience testing the validity of proposed new approach of Special Relativity using Perplex Numbers.
Definitions
Perplex Numbers also known as Split Complex numbers or double numbers possess two real components x and y and written in ordered pair as (x,y) where j = −1unlike i = −1 .
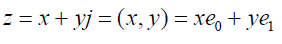 (1)
(1)
And its conjugate is defined as;
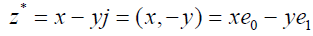 (2)
(2)
Its unit basis vectors in determinants form may be written as;
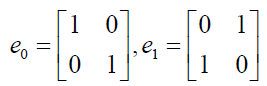 (3)
(3)
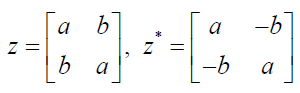 (4)
(4)
The obvious properties of these basis vectors are;
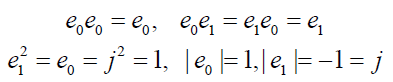 (5)
(5)
Here, e_0 is 2×2 unit matrix (I). A perplex number and conjugate of another number may be expressed as;
 (6)
(6)
Product of such a pair is an entity of special physical significance, which may be defined in general as follows;
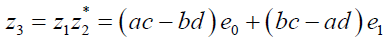 (7)
(7)
Moreover, the self product of a perplex number may be used to
express length of that number. In perplex numbers, |z1| may be
regarded as length of the perplex number which can be used for analogous Euler’s representation for 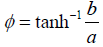 as following;
as following;
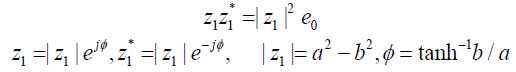 (8)
(8)
The collection D of all complex numbers z = x + yj : x, y∈R (where j2 =1), forms an algebra over the field of real numbers. The two perplex numbers z1 and z1 have product z1 z2 that satisfies N(z1 z2) = N(z1 )N(z2) . Similar algebra based on square and component-wise operations of addition; multiplication offers a quadratic form over R2. The ring isomorphism;
D→ R2 : x + yj (x + y, x − y)
relates proportional quadratic forms but mapping is not isometric. The multiplicative inverse of a perplex number z1 may be denoted as z1-1 may be expressed as follows;
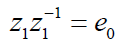 (9)
(9)
to obey relationship 1 z1z1-1 = e0 which is a unit matrix, provided |z1|≠ 0 .
Event in Perplex numbers (Z)
To explore the quantities of Special Relativity using Split Complex Numbers, we shall substitute a = ct and b = r for defining an event or space-time position Z. In fact, we propose hypothesis that time is real and space is imaginary in perplex number or split complex numbers representation. Here, we differ with the idea mentioned by Carbajal wherein time is considered as an imaginary quantity [7]. Similarly, an offbeat reporting is also found in the literature where the speed of light is treated imaginary by Mehran Rezaei [8].
We now propose to represent time and space using perplex numbers as;
 (10)
(10)
where;  Now, the
modulus or length of Z denoted by |z| may be expressed as;
Now, the
modulus or length of Z denoted by |z| may be expressed as;
 (11)
(11)
Where, the product of perplex number and its conjugate ZZ* depicted in equation over matrix multiplication appears as;
 (12)
(12)
Here r/t resembles velocity u of the material object which ranges
of 0..c confining the term relative velocity u/c ranging over 0..1.
Figure 1 depicts variation of Euler angle φ as a function of
relative velocity u/c over possible range from 0 to 1. Moreover,
Figure 2 depicts a cone that represents present universe cone
along with the grid lines that is composed of hyperbolic curves
c2t2 − r2 = 0,±12 ,±22 ,...and by a horizontal line inclined at angles
φ = 0,±0.25,±0.50,±0.75,±0.99.. The stationary objects will be
represented by a horizontal line having 0° angle to x-axis or say t-axis c = 1. The moving objects are represented by inclined
lines bearing angle φ that is ranging over 0 − 45°. The fastest
propagation represented by v = c is by the line inclined at 45°.
The uncharted carpet in the plane is absolutely separated. Thus,
we have a perplex environment that offers a quantity called
modulus or length of a perplex numbers that is Lorentz Invariant i.e.,  which is defined in relativity as the
interval in the space-time continuum. This is a fascinating form of
perplex numbers as all inertial observers agree upon this quantity
making this number universal. The product ZZ* possesses only
real part that is determined by the determinant of Z* or Z* which
we regard in terms of length of perplex number. Note that the
associated component is the Euler angle
which is defined in relativity as the
interval in the space-time continuum. This is a fascinating form of
perplex numbers as all inertial observers agree upon this quantity
making this number universal. The product ZZ* possesses only
real part that is determined by the determinant of Z* or Z* which
we regard in terms of length of perplex number. Note that the
associated component is the Euler angle  that makes
its description
that makes
its description  complete and meaningful.
complete and meaningful.
The significance of the Euler’s angle  in the event can
be understood as following:
in the event can
be understood as following:
When ct > r the event is time-like  UNIVERSE
UNIVERSE
When ct > r the event is space-like  REMOTE
REMOTE
When ct > r the event is light-like  path of em radiation
path of em radiation
Note that:  is a shorthand way of expressing
perplexes number without the loss of generality.
is a shorthand way of expressing
perplexes number without the loss of generality.
Lorentz transformation as a Perplex number
From Special Relativity we know the Lorentz Transformation equations ct' =γ (ct − βr) and r' =γ (r − βct). We can explore matrix representation to express it as;
 (13)
(13)
The Lorentz Transformation is a perplex number and in matrix form it can be expressed as;
 (14)
(14)
The above equation of Lorentz transformation is also a perplex number and can be expressed in the ordered pair as LT = (γ,−βγ) . The complex conjugate of this Lorentz Transformation perplex number LT −1 = LT* = (γ ,βγ) can be regarded as Inverse Lorentz Transformation. Obviously, when perplex number multiplied with its conjugate offers unity.
 (15)
(15)
Moreover, it is worth mentioning here that the matrix operator - Lorentz Transformation offers number length unity which in fact keeps the perplex numbers unaltered over multiplication; |LT|=1 =|LT*|. Thus, the Lorentz invariance in Special Relativity can be re-looked in perplex numbers easily as the perplex number multiplied by unity. However, it offers a new perplex complex number with same modulus but different Euler’s angle for another inertial observer.
 (16)
(16)
If one desires to speak in terms of hyperbolic angle φ the
trigonometric identity  offers us (i) tanhΦ = β (ii) coshΦ =γ and (iii) sinhΦ = βγ. It
offers geometric version of Lorentz Transformation equation as
tanhφ = β as following:
offers us (i) tanhΦ = β (ii) coshΦ =γ and (iii) sinhΦ = βγ. It
offers geometric version of Lorentz Transformation equation as
tanhφ = β as following:
 (17)
(17)
 is also a perplex number like
equation (1) and thus we have e− jΦ = coshΦ − jsinhΦ that
represents in fact the Lorentz boost. Thus, the Euler’s like identity
in perplex numbers offers us an elegant Lorentz Transformation
equation and its inverse as;
is also a perplex number like
equation (1) and thus we have e− jΦ = coshΦ − jsinhΦ that
represents in fact the Lorentz boost. Thus, the Euler’s like identity
in perplex numbers offers us an elegant Lorentz Transformation
equation and its inverse as;
 (18)
(18)
for obvious notation ejφ' = coshφ' + jsinhφ' and the hyperbolic
angle  . The quantities of transformed perplex
numbers bears following identities.
. The quantities of transformed perplex
numbers bears following identities.
 (19)
(19)
Interpretation of |LT|: After exercising |LT| on |Z| we obtain |Z'| and φ'.
 (20)
(20)
This offers us an important conclusion regarding invariance of relativistic interval as following;
 (21)
(21)
Interpretation of φ' : The Euler’s angular component  . Now for φ' we can write;
. Now for φ' we can write;
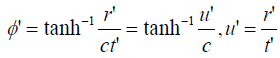 (22)
(22)
Substituting 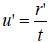 and
and 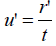 in the last equation, we get
in the last equation, we get
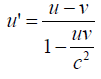 (24)
(24)
Now, exercising inverse Lorenz transformation 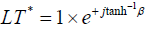 on event Z will offers us the same formula for modulus as in the
equation (21). While the Euler angle is on the similar lines of
equation (24) with a difference of sign as;
on event Z will offers us the same formula for modulus as in the
equation (21). While the Euler angle is on the similar lines of
equation (24) with a difference of sign as;
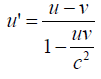 (25)
(25)
The above equation (25) is the Composition of Velocity in Special Relativity. We shall revisit Composition of Velocity in Article 6 separately as a consequence of Lorentz boost to to develop consequences of Perplex Number Special Relativity.
Geometrical Interpretation of φ ' : The Lorentz transformation in Euler’s form;
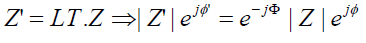 (26)
(26)
As |Z'|=|Z| we have;
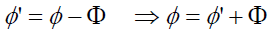 (27)
(27)
Operating tanh−1 on both sides and substituting
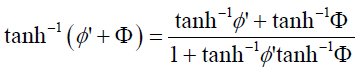 .
.
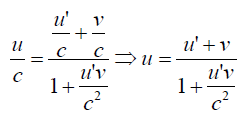 (28)
(28)
Thus, we arrive at the velocity composition through the addition of the hyperbolic angle.
Relativistic Kinematics using Perplex Numbers
To establish kinematics of Special Relativity as developed by Landau and Lifshitzs [9,10] in terms 4-vectors of perplex numbers. Consider an event represented in frame S and S’ which forms a pair of inertial frames with all usual contentions and arguments established in the subject. An event or perplex position can be represented by Z = ct + rj and dZ = cdt + drj which are related by Lorentz Transformation equation (13). By definition, an infinitesimal interval which in another words is length of perplex numbers is invariant for all inertial observers. We have dZ = cdt + drj and dZ' = cdt' + dr'j.
 (29)
(29)
Now we impose that the event occurs at the origin of the coordinate system so that t'. This will simplify the last equation as;
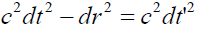
Changing over notation t' to τ and substituting dr / dt = v(t),
β (t) = v / c and 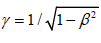 and simplifying we get;
and simplifying we get;
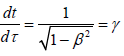 (30)
(30)
Thus, the Lorentz factor γ represents the rate at which time t changes with respect to proper time v. Here v is regarded as relative velocity between two inertial frames S and S’.
Position ( Z ) using Perplex Numbers: The relativistic event can be expressed in perplex number space-time representation as in (10) its complex conjugate can be expressed as (11) while its modulus can be expressed as (12). Note that: The Lorent transformation equation may be written as Z' = LT.Z and it yields Lorentz invariance for the quantity |Z'Z'*|=|ZZ*|= (c2t2 − r2)2 and φ' = tanh−1(u' / c) .
Velocity ( ) using Perplex Numbers: We shall define perplex velocity by differentiating perplex position with respect to the proper time which is a universal quantity for all inertial observers.
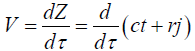 (31)
(31)
Substituting dt / dτ =γ and dr / dτ =γ dr / dt =γ v, we get;
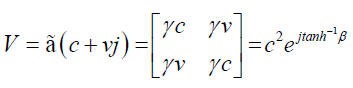 (32)
(32)
Note that here v is the usual velocity by definition. The varied forms in which the Velocity using perplex number or simply perplex velocity may be written are as follows;
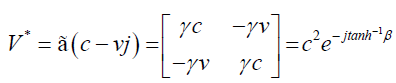 (33)
(33)
Its conjugate 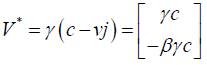 on multiplication with V
offers an invariant quantity or length of perplex number
c2 as
depicted below.
on multiplication with V
offers an invariant quantity or length of perplex number
c2 as
depicted below.
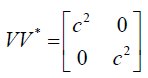 (34)
(34)
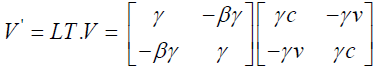 (35)
(35)
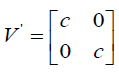 (36)
(36)
Note that: The Lorentz transformation equation may be written as V' = LT.V and it yields Lorentz invariance |V'V'*|=|VV*|= c4 . Thus, operating unit length perplex number LT retains the length of the perplex number on which it is operated i.e., perplex velocity. The invariance governing equation |V|=|V'|= c2 is same for all inertial observers which are in fact the universal constant.
Momentum (P) using Perplex numbers: We shall define perplex momentum by multiplying mass (a scalar number) with perplex velocity.
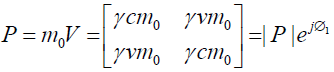 (37)
(37)
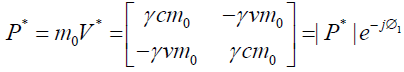 (38)
(38)
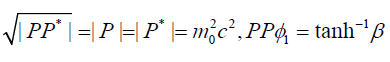 (39)
(39)
Its conjugate P* on multiplication with P offers an invariant quantity or length of perplex number m02c2. Here m0 is proper mass which is an essentially universal quantity that all inertial observers can agree upon and ym0 = m;
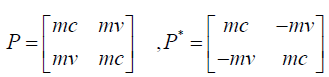 (40)
(40)
The varied forms in which the momentum using perplex number or simply perplex momentum may be written are as follows;
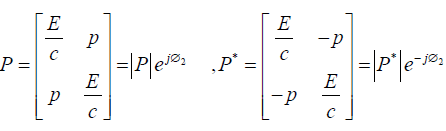 (41)
(41)
Here, in the last equation we propose to rewrite the perplex momentum equation (39) wherein the real part mc = E / c is abstract of Einstein’s most famous equation E = mc2 and imaginary part mv is usual relativistic momentum p. The complex conjugate multiplication now offers us a form as below;
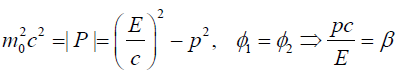 (42)
(42)
Comparing 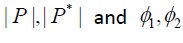 from equations (39) and (42)
followed by few steps of simplification, we get the expression for
relativistic energy of a particle as;
from equations (39) and (42)
followed by few steps of simplification, we get the expression for
relativistic energy of a particle as;
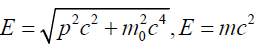 (43)
(43)
Note that: The Lorentz transformation equation may be written as P' = LT.P and it yields Lorentz invariance P'P'* = PP*,| LT |= 1.
The obvious relationship governing Lorentz transformation is as follows:
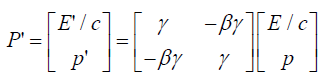 (44)
(44)
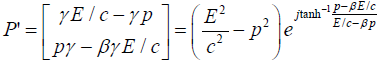 (45)
(45)
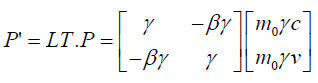 (46)
(46)
Similarly, we can write;
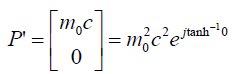 (47)
(47)
While the perplex momentum (p) is expanded form appears as follows.
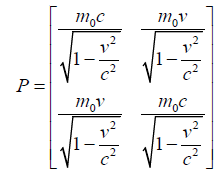 (48)
(48)
In above equation we have used a substitution 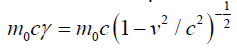 on binomial expansion and
simplification gives
on binomial expansion and
simplification gives 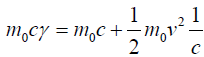 . Adjusting c to look
for rest energy and kinetic energy we have following equation.
. Adjusting c to look
for rest energy and kinetic energy we have following equation.
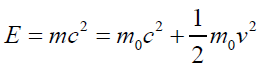 (49)
(49)
Acceleration (A) using Perplex numbers: We shall define perplex acceleration by differentiating perplex velocity with respect to the proper time (τ).
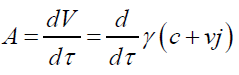 (50)
(50)
Substituting dt / dτ =γ and d / dτ =γ d / dt, we get:
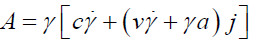 (51)
(51)
Note that here a is the usual acceleration by definition and γ is time derivative of γ. The varied forms in which the Acceleration using perplex number may be written are as follows:
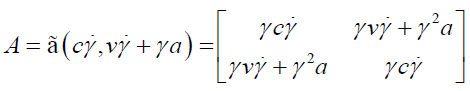 (52)
(52)
The above may be further simplified after substituting the identity
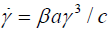 and its simplification take following form;
and its simplification take following form;
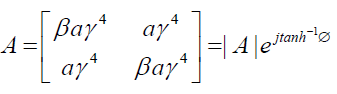 (53)
(53)
A little mathematical exploration will enable to arrive at following invariant quantities like other pairs (ZZ*,VV*, and PP*) offered are new findings.
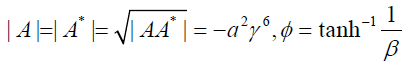 (54)
(54)
Note that: The Lorent transformation equation may be
written as A' = LT.A and to yield Lorentz invariance 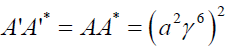 . We shall explore perplex acceleration
under Lorentz Transformation equation.
. We shall explore perplex acceleration
under Lorentz Transformation equation.
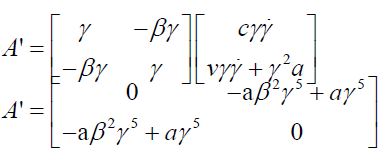 (55)
(55)
Thus, the above discussion yields out information regarding
acceleration in perplex numbers and length of perplex
acceleration that remains invariant under Lorentz Transformation is 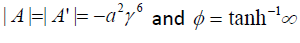 .
.
Force (F) using Perplex numbers: We shall define perplex force by differentiating perplex momentum with respect to the proper time (τ).
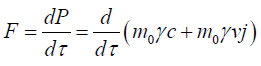 (56)
(56)
Substituting dt / dτ =γ and d /dτ =γ d/dt, we get:
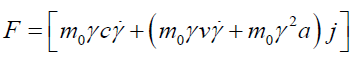 (57)
(57)
Note that here is a the usual acceleration by definition and time
derivative of bearing relationship 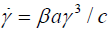 . The varied forms
in which the Force using perplex number or simply perplex force
may be written are as follows:
. The varied forms
in which the Force using perplex number or simply perplex force
may be written are as follows:
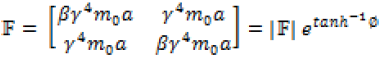 (58)
(58)
Here, 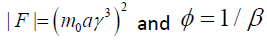 leads to the Euler’s form of
Perplex force.
leads to the Euler’s form of
Perplex force.
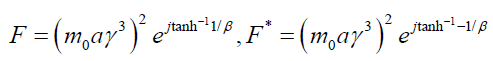 (59)
(59)
Note that: The Lorent transformation equation may be written as F' = LT.F but is is observed that it disobeys Lorentz invariance for Newtonian Force |F|=|F'| and F'F'* = FF*. To express it more obviously we shall explore perplex force under Lorentz Transformation equation.
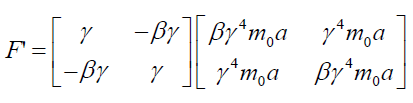 (60)
(60)
On solving the product and exploring simplification, we get;
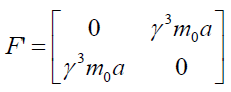 (61)
(61)
Thus, the above discussion yields out information regards force in perplex numbers and length of perplex acceleration that remains invariant under Lorentz Transformation. Thus, we conclude following:
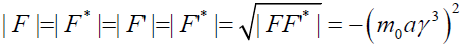 (62)
(62)
From equation (62) we can write Euler’s form as;
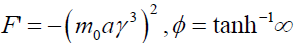 (63)
(63)
Another Approach: Combining equations (41) and (56) we can re-assemble another from for equation as;
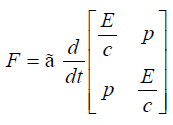 (64)
(64)
From mechanics we know dE /dt = fv = m0a'v and dp/dt = m0a', we get;
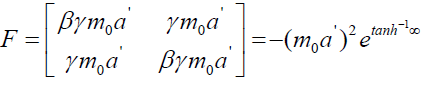 (65)
(65)
The Lorentz transformation of above equation on simplification offers following form along with its Euler’s representation;
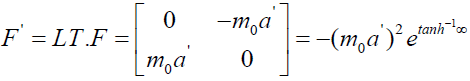 (66)
(66)
Now comparing equations (66) and (63) we can conclude following.
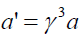 (67)
(67)
This is in agreement with the findings of acceleration by Rindler [11-13] in 1966.
Velocity composition
Let an observer A is in an inertial frame S measures space-time coordinates of an event as; Z = (ct, r). Another inertial observer B (say in frame S’) records the same event denoted as Z' = (ct', r') is moving with relative velocity β1 = v1/c with respect to observer A (i.e., frame S). The concerned hyperbolic angle in analogous Euler’s representation be φ1. Now let us consider the third observer C is moving with relative velocity β2 = v2/c with respect to observer B (say frame S’). The concerned hyperbolic angle be φ2. Now, with respect to A, let the resultant relative velocity be β = v / c and the concerned hyperbolic angle, say φ will obviously be the sum of the first two angles φ =φ1 +φ2.
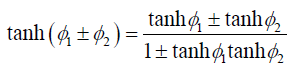 (68)
(68)
But for the definition, we know; tanhφ = β , tanhφ = β1, tanhφ = β2 which leads to the manner in which relative velocities can be added.
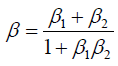 (69)
(69)
The above equation is consistent with findings of Einstein’s Special Relativity [2,10].
Consequences of Lorentz boost
Let a pair of events charts with a complex number be expressed as Z1 = ct1 + r1j and Z2 = ct2 + r2j in frame S. Now we shall look for the effect of Lorentz boost to offer a look at view of a observer moving with uniform velocity along -axis referred as an inertial frame S' . The same pair of events may be chart with a complex number be expressed as Z1 ' = LT.Z1 and Z2 ' = LT.Z2 in frame S'. The observer in S' measures interval between two events as dZ2' = Z2 '− Z1 ' .
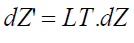 (70)
(70)
The explicit expanded form of the above equation looks as follows:
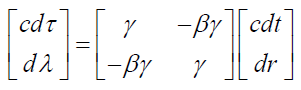 (71)
(71)
Comparing real and imaginary parts we get following pair of equations which we are interested in exploring.
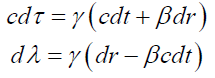 (72)
(72)
The time dilation: Let the two events occur at same location dr = 0 and differ only in time (real part). For example, a flash of light occurring at same place after a time interval. Comparing real-part of the last equation (72) and simplifying for dr = 0 for real part, we get:
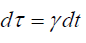 (73)
(73)
This relation (73) depicts time dilation suggested by Einstein’s Special Relativity [2,10].
The space contraction: Let the two events occur at time location dt = 0 and differ only in space location dr. For example, measuring length of a rod at a moment of time. Comparing imaginary-part of the last equation (72) and simplifying for dt = 0, we get:
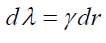 (74)
(74)
Let the two events occur at same time and differ only in space location which is imaginary part in complex number representation of events. Let the observer in frame S’ measure length that is stationary relative to the rod. Hence, we define this length as a proper length dλ = l0 . The rod moving parallel to its length will appear of length dr = l(v) given by expression:
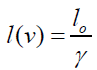 (75)
(75)
The above relation (25) depicts length contraction as suggested by Einstein’s Special Relativity [2,10].
Simultaneity is relative: Now we shall deal with the issue of simultaneity in special relativity. We shall again explore pair of equations (72) and per-conceive that two events are occurring at two different spatial locations and are simultaneous in frame S. Imposing dr ≠ 0 and dr ≠ 0 , we get
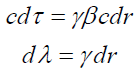 (76)
(76)
For this event to be simultaneous in frame S' , i.e., dr = 0 it is essential that dr = 0. It means that two events simultaneous in one inertial frame does not guarantee that it will be simultaneous for other inertial observers. For absoluteness of simultaneity, the event should not only be simultaneous in one frame but also must occur at the same location.
Velocity in moving frame: To add velocities together, consider a physical situation accordingly.
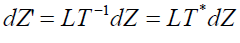 (77)
(77)
The explicit expanded form of the above equation looks as follows:
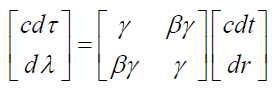 (78)
(78)
Comparing real and imaginary parts we get following pair of equations which we are interested in exploring.
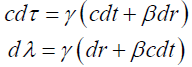 (79)
(79)
Consider ratio of latter to the former equation in the last equation (79), with substitutions; u'(τ ) = dλ / dτ is velocity in frame S', u(t) = dr / dt is velocity in frame S:
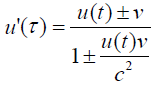 (80)
(80)
Thus, perplex numbers offer the velocity addition formula by another approach also. Another version for subtracting velocities can also be raised from the analogous equation; dZ' = LT.dZ that offers us another equation depicted in equation (80) with minus sign.
Acceleration in a moving frame
Differentiating one of the equations (80) with respect to and exploring the equation (30)
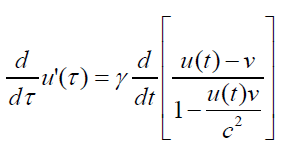 (81)
(81)
Substituting 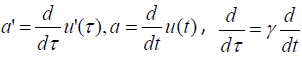 and simplifying
we get:
and simplifying
we get:
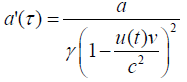 (82)
(82)
For slow speed considerations we can employ u(t)v ≈ v2 and induct γ accordingly to further simplify the equation:
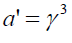 (83)
(83)
Acceleration leading to Rindler space
We have established acceleration in moving frame as γ3a which on comparison with the spatial component of acceleration arising from equations (52) offers us:
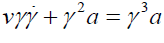 (84)
(84)
The above equation (84) resembles acceleration leading to Rindler space [12-16]. Note that A = a0 + a1j wherein we refer a0 as temporal and a1 as spatial components. Simplifying the last equation and replugging derivative notations to look for the differential equation version, we get:
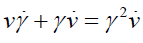 (85)
(85)
The above equation leads to the Rindler space on the line of traditional equation here aroused from the perplex acceleration component. The equation (63) may further be modified in reference to the last equation (85) as follows:
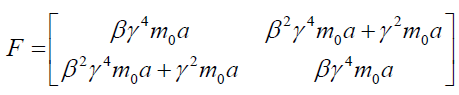 (86)
(86)
The Euler’s form of above equation is;
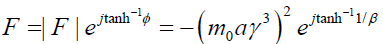
Applications of Perplex numbers
With minimal mathematical resources, we can quickly apply the quantities raised for a couple of well-known Special Relativity applications to try hands-on with perplex numbers.
A free electron cannot absorb a photon: The perplex momentum
of free electron at rest can be expressed as; prest = m0ce0 + 0e1.
Note that the Lorentz factor γ =1 for electron at rest. We shall
define perplex momentum for a photon as 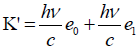
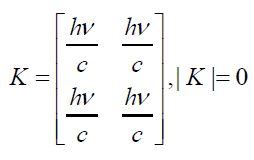 (87)
(87)
We consider (hypothesis) that the free electron at rest absorbs a photon and moves with some energy as shown in Figure 3. The perplex momentum of moving electron may be expressed as;
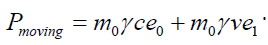
The perplex momentum conservation will be simply expressed as:
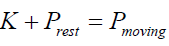 (88)
(88)
In matrix notations
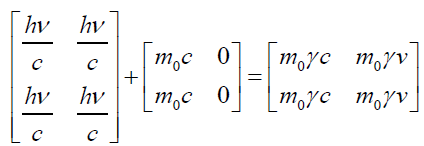 (89)
(89)
The perplex number length by definition can be compared as follows.
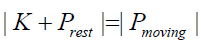 (90)
(90)
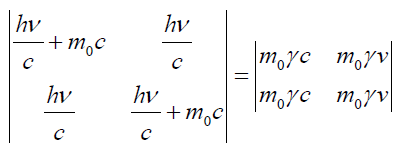 (91)
(91)
On simplification of above equation, we get equation (92) which is invalid and it is the outcome of the hypothesis - a free electron absorbs photon.
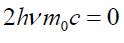 (92)
(92)
The above equation is invalid as product of non-zero quantities can never vanish. The invalidity of above equation supports the fact that "A free electron cannot absorb a photon".
Berkley collider: Consider a proton at rest hit by a moving proton
so that after collision the product contains 4-protons. We are
looking for the energy of the proton with which it is allowed to
collide upon a rest proton so that 4-protons at rest are created
i.e., resultant product is 4 particles. Moreover, we anticipate
that the product 4-particles created are at rest. Figure 4 depicts
the schematic representation of proton-proton interaction to result 4-protons at rest. Let  is the momentum of
incident proton on a rest proton P2 =m0ce0+ 0e1 resulting into 4 protons at rest P3 =4m0ce0+ 0e1. The conservation equation
will be:
is the momentum of
incident proton on a rest proton P2 =m0ce0+ 0e1 resulting into 4 protons at rest P3 =4m0ce0+ 0e1. The conservation equation
will be:
 (93)
(93)
Finding the perplex number length, we get
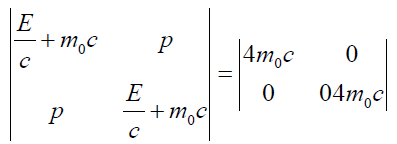 (94)
(94)
On simplifying the above equation to obtain the energy required for above reaction, we get:
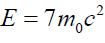 (95)
(95)
Thus, we need to bombard a proton with energy 7m0c2 on a proton at rest to result into 4-protons at rest, as per nuclear reaction referred Berkley Collider.
Compton’s Effect versus Quantum Doppler Effect: In Compton’s effect we considered free electron presumed to be in the resting state that scatters photon. The perplex momentum of free electron to be at rest P and the incident photon K can be expressed as follows:
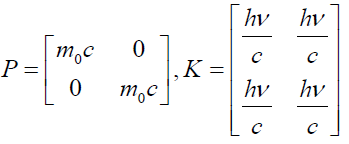 (96)
(96)
Note that the Lorentz factor γ =1 for the electron at rest. 1D restriction to space makes us consider scattered photon travels with smaller frequency p while electron recoils with momentum p in the restricted 1D space. The perplex momentum governing the particles after collision can be expressed as
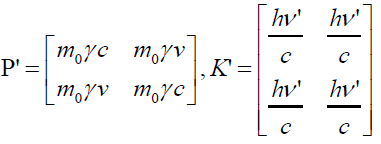 (97)
(97)
The obvious perplex momentum conservation equation (equating perplex momentum before and after collision) is expressed as:
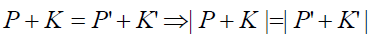 (98)
(98)
Raising the matrix form of the above expression and simplifying it we get:
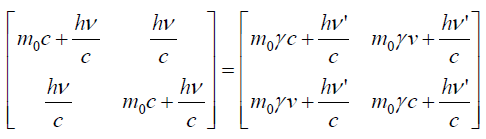 (99)
(99)
A few steps of simplification of the determinant of the above matrix equation renders length of the perplex numbers comparison to yield out the famous equation governing the 1+1 D Compton’s shift as:
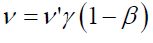 (100)
(100)
Further simplifying it to a form that resembles quantum version Doppler Effect
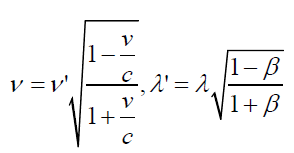 (101)
(101)
4D Considerations in Compton’s effect: In Compton’s effect, we presume electron in carbon block at rest state that scatters photon in the direction φ and the recoils electron at an angle θ to the direction of incidence (x-axis). Figure 5 depicts the schematic representation of photon scattered by electron in carbon block hypothesized at rest. The perplex number expression may be modified as follows [14-19]: The perplex momentum of the free electron at rest, P and the incident photon K traveling along x-direction can now be expressed in 1+3 dimensions as follows:
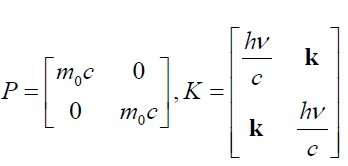 (102)
(102)
Here, we propose null momentum vectors 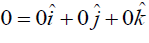 for
the electron at rest and
for
the electron at rest and 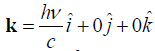 for the approaching
photon. Note that the Lorentz factor γ =1 for the electron.
After scattering the photon travels at an angle φ with smaller
frequency ν ' while the electron recoils at an angle θ with
momentum p. The perplex momentum governing the particles
accounting 4D parameters may be expressed as:
for the approaching
photon. Note that the Lorentz factor γ =1 for the electron.
After scattering the photon travels at an angle φ with smaller
frequency ν ' while the electron recoils at an angle θ with
momentum p. The perplex momentum governing the particles
accounting 4D parameters may be expressed as:
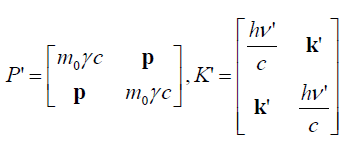 (103)
(103)
Here, momentum vectors for recoil electron ![]() for p = m0γv i.e., relativistic momentum
and
for p = m0γv i.e., relativistic momentum
and 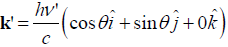 is momentum vector associated
with scattered photon. The obvious perplex momentum
conservation equation (equating perplex momentum before and
after collision) which is in 4D version now may be expressed as:
is momentum vector associated
with scattered photon. The obvious perplex momentum
conservation equation (equating perplex momentum before and
after collision) which is in 4D version now may be expressed as:
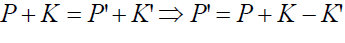 (104)
(104)
Raising the matrix form of the above expression and simplifying it we get:
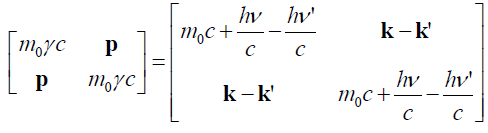 (105)
(105)
Here, while finding determinant of the matrix, we have to work
out the inner product of the vectors as 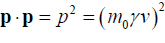 ,
, 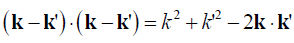 for obvious
for obvious 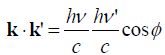 ,
, 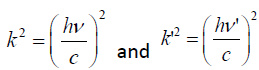 Working out the determinant of
the above matrix equation that renders length of the perplex
numbers comparison to yield out the famous equation governing
the Compton’s shift as [20-23]:
Working out the determinant of
the above matrix equation that renders length of the perplex
numbers comparison to yield out the famous equation governing
the Compton’s shift as [20-23]:
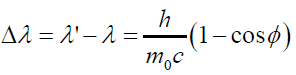 (106)
(106)
The time-space warp suggested by Einstein in 1905 has been
configured in the present work as a real part and imaginary part
in perplex number form. This research confirms a space-time
warp that looks like the Rindler space-time cone. Interestingly it
resembles with space-time warp inside the Schwarzschild radius
of a black-hole. The present approach of perplex numbers satisfies
all facets of the theory of special relativity and its implications also. The distance of a point from or iz in 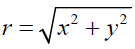 invariant in a frame rotating about -axis. Unlikely, SR suggests
that interval of format
invariant in a frame rotating about -axis. Unlikely, SR suggests
that interval of format 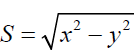 remains invariant. The
pefficient and easy handling. This approach smoothly sails like a
4-vectors treatment but offers an advantage. It further possesses
potential of exploring real problems in special relativity using
perplex numbers. The success of perplex number exploration
justifies its hypothesis that time is real and space is imaginary.
remains invariant. The
pefficient and easy handling. This approach smoothly sails like a
4-vectors treatment but offers an advantage. It further possesses
potential of exploring real problems in special relativity using
perplex numbers. The success of perplex number exploration
justifies its hypothesis that time is real and space is imaginary.