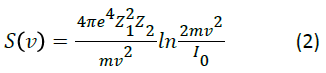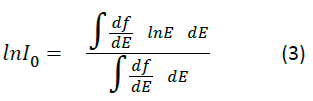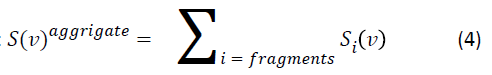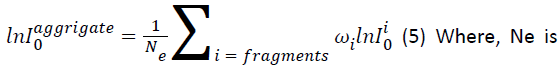British Journal of Research Open Access

Editorial

Since it was first determined that cancers could be treated with radiation, it has been of interest to determine the effects of various types of radiation on biological systems. Originally, X-rays were used. However, the dose (amount of energy from the radiation) deposited in tissue as a function of depth from the tissue surface decreases slowly, as shown in Figure 1. Thus there is energy deposition in other tissue surrounding the cancer which can cause collateral damage.

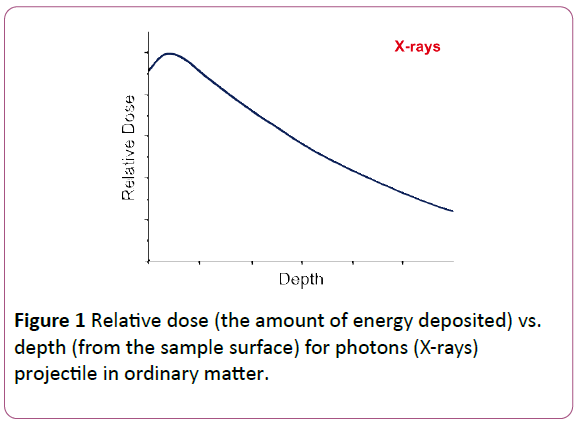
Figure 1: Relative dose (the amount of energy deposited) vs. depth (from the sample surface) for photons (X-rays) projectile in ordinary matter.

However, particle radiation, using charged particle projectiles, such as protons instead of photons, has been shown to have a large advantage, as the energy deposited by baryonic projectiles is much more localized than that from photons such as X-rays, as shown in the Figure 2.

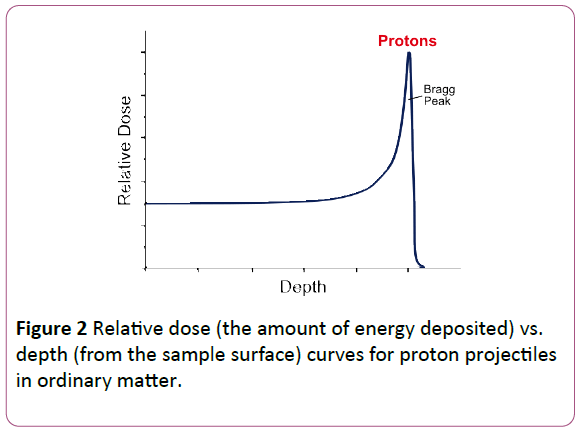
Figure 2: Relative dose (the amount of energy deposited) vs. depth (from the sample surface) curves for proton projectiles in ordinary matter.

Thus, the deposition of energy from the radiation can be much more accurately focused on the specific area of treatment. The question remains as to whether different tissues absorb proton radiation differently.

The effect of radiation on a target such as a biomolecule first involves transfer of projectile kinetic energy to target electronic energy, which can then lead to target fractionation and subsequent loss of function.

The crucial quantity to be considered [1] is the ability of the target to absorb energy from the projectile and referred to as the stopping power of the target, and is the energy loss of the projectile per unit length traveled in the target at projectile velocity In order to normalize for target particle density variation, the stopping power is divided by the target particle density, N, yielding the target’s density independent stopping cross section

Here,

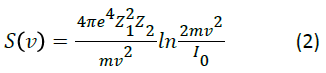
Where, Z₁ and Z₂ are the projectile charge and target electron number. I_o is the mean excitation energy of the target, which measures the ability of a target molecule to absorb energy from a projectile ion, and is determined from the target dipole oscillator strength distribution (f):

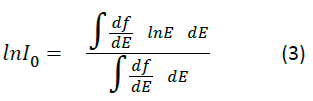
One of the most important molecules considered in radiation of tissue is simply water. As water is a reasonable simple molecule, calculations can be done on it directly [2] using equation 3 and sophisticated quantum molecular calculations. Such calculations give a value of the mean excitation energy of water to be 73.0 eV [2].

The problem is that many biological systems are large by molecular standards and made up of various components. These conditions make computation of either the stopping properties or the mean excitation energy of such a system difficult, due to its size and complexity [3].

However, there is an approximation that works quite well in the biologically related fields of stopping, where molecular target systems are quite large. Introduced at the beginning of the last century by William Henry Bragg [4], it is known as Bragg’s Rule, and states that the stopping cross section of an aggregate system, such as a biological molecule, S(v) aggregate, may be determined from a weighted sum of the fragment stopping cross sections Si(v), where the fragments may be individual atoms or polyatomic molecular fragments, according to

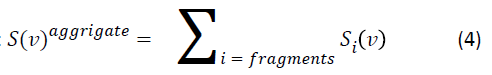
As the stopping cross section can be easily related to the mean excitation energy as in equation 2, the mean excitation energy of an aggregate can also be extracted from the mean excitation energies of the fragments [5]:

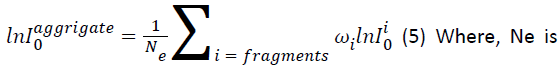
the total number of electrons in the aggregate system, and ω_i is the electron number of fragment i.

An example of the Bragg Rule applied to some amino acid follows, where some previously calculated mean excitation energies of some amino acids [3,5] are reported in the table [6]. An amino acid may be written as H₂NCHRCOOH, or A-R, where A is CH(NH₂)COOH. I_A has been determined to be I_A=78.8 eV with ω=38 for the amino acid common fragment [3].

The Table gives the mean excitation energies (I) for several amino acids thus calculated (Table 1).

Amino Acid	R	I0 (eV)
Glutamine	-(CH2)2-CO-NH2	71.8
Phenylalanine	- CH2 -Phe	74
Tyrosine	- CH2 –Phe-OH	66.8
Lysine	-(CH2)4-NH2	65.3
Glycine	-H	74
Alanine	0	72
Serine	-CH2-OH	74
Glutamic Acid	-(CH2)2-COOH	67.4
Aspartic Acid	-CH2-COOH	69.4
Threonine	-CHOHCH3	70.9
Leucine	-CH2-CH(CH3)2	63.4
Asparagine	-CH2-CO-NH2	74.4
Isoleucine	-CHCH3-CH2-CH3	63.4
Valine	-CH(CH3)2	65.0

Table 1: Calculated Mean excitation energies of some amino acids.

The mean excitation energies in the table are reported in references [3,5], where the details of their calculation can be found.

The mean excitations of the amino acids appear quite similar. In the treatment described above, details of molecular connectivity and molecular conformation are not considered, as the mean excitation energy calculated with a Bragg-like rule depends only on the compositions of the various fragments that make up the molecule and not on their arrangement.

Thus, for example, the mean excitation energies of leucine and isoleucine are calculated to be the same, as they differ only in connectivity and conformation. However, for complex systems, the Bragg Rule scheme works well and produces stopping power data in good agreement with experiment [3,5].

One notes also that amino acids and other compounds found in tissue are composed of the same atoms and differ primarily in atom number and connectivity. Thus they are expected, in the Bragg approximation, to have similar mean excitation energies and stopping powers. As the stopping power of a sample depends on the logarithm of the stopping molecule (equation 2), and as the mean excitation energy of water, the other large component of tissue, is similar (73 eV., [2]), only reasonably small differences in proton stopping powers of different tissues would be expected.

References

1. Andreo P (2009) On the Clinical Spatial Resolution Achievable with Protons and Heavier Charged Particle Radiotherapy Beams.  Phys Med Bio 54: N205-N215.
2. Geertsen J, Oddershede J, Sabin JR (1986) Calculation of Mean Excitation Energies via the Polarization Propagator Method.  H2 and H2O. Phys Rev A 34: 1104.
3. Sauer SPA, Oddershede J, Sabin JR (2011) Mean Excitation Energies for Biomolecules: Glycine to DNA. Adv Quantum Chem 62: 215.
4. Bragg WH, Kleeman R (1905) On the Alpha Particles of Radium and Their Loss of Range in Passing through Various Atoms and Molecules. Philos Mag 10: 318.
5. Bruun-Ghalbia S, Sauer SPA, Oddershede J, Sabin JR (2010) Mean Excitation Energies and Energy Deposition Characteristics of Bio-Organic Molecules. J Phys Chem B 114: 633.